3.4. Мгновенная угловая скорость и угловое ускорение. Кинематические уравнения Эйлера

Твердое тело с одной неподвижной точкой в общем случае участвует одновременно в трех вращениях, векторы угловых скоростей которых с использованием углов Эйлера имеют вид:

– вектор угловой скорости прецессии;

– вектор угловой скорости нутации;

– вектор угловой скорости ротации (собственного вращения).

Здесь – единичные орты осей вращения OY, OE, Oy соответственно (рис. 3.8, 3.12). Поскольку названные оси пересекаются в точке О, то абсолютное движение тела в каждый момент времени есть вращение вокруг мгновенной оси, проходящей через точку пересечения вышеназванных осей с мгновенной угловой скоростью , равной геометрической сумме векторов угловых скоростей составляющих:

. (3.26)

Р ис. 3.12

Ось, совпадающая с вектором , является мгновенной осью вращения твердого тела вокруг неподвижной точки О. Мгновенная ось вращения представляет собой геометрическое место точек тела, скорости которых в данный момент времени равны нулю.

Мгновенная угловая скорость меняется с течением времени как по величине, так и по направлению. Это изменение определяется производной по времени от угловой скорости и называется мгновенным угловым ускорением тела:

, (3.27)

или , где – составляющая , направленная вдоль мгновенной оси вращения и характеризующая изменение по величине; – составляющая , перпендикулярная вектору и характеризующая изменение по направлению ( ). Вектор мгновенного углового ускорения будем откладывать от неподвижной точки О тела (рис. 3.13).

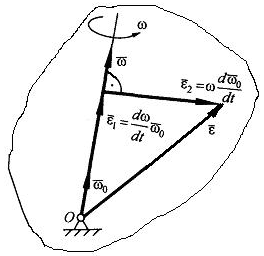
Рис. 3.13

Алгебраические величины проекций вектора (3.26) на оси подвижной системы координат Oxyz (рис. 3.8), единичные орты которой соответственно,

. (3.28)

Согласно (3.26),

.

Разложение единичного вектора по базису [x]_п , как следует из формул (3.15) и (3.25), таково:

. (3.29)

Единичный вектор , как следует из (3.20) и (3.21), можно представить в виде

. (3.30)

Подставляя (3.29) , (3.30) в соотношение (3.26), получаем

Таким образом, искомые проекции вектора угловой скорости на оси подвижной (связанной с телом) системы координат будут равны

или (3.31)

Полученные соотношения носят название кинематических уравнений Эйлера. Они устанавливают связь между проекциями вектора угловой скорости тела , углами Эйлера и их первыми производными по времени.

3.5. Скорость и ускорение точек тела. Формула Ривальса

Скорость любой точки тела в случае его сферического движения можно найти из формулы Эйлера:

. (3.32)

М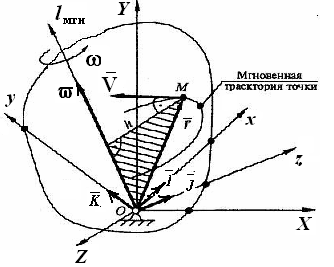 одуль скорости точки тела , где h – кратчайшее расстояние от рассматриваемой точки до мгновенной оси вращения (рис. 3.14). Таким образом, при сферическом движении твердого тела вокруг неподвижной точки, как и при его вращении вокруг неподвижной оси, скорости точек тела в данный момент времени пропорциональны расстояниям h.

Рис. 3.14

Вектор скорости точки тела перпендикулярен плоскости, в которой лежат векторы и (заштрихованная плоскость на рис. 3.14), т.е. перпендикулярен h и направлен по касательной к мгновенной траектории точки в сторону угловой скорости тела, вращающегося вокруг мгновенной оси.

Если в данный момент времени скорость точки тела , то ее ускорение .

С учетом (3.32) можно записать,

.

Поскольку , то

. (3.33)

Полученное соотношение называют формулой Ривальса. Ускорение есть геометрическая сумма двух составляющих: – вращательное ускорение; – осестремительное ускорение.

Таким образом,

. (3.34)

В ектор вращательного ускорения направлен перпендикулярно к плоскости, в которой лежат векторы и (заштрихованная плоскость на рис. 3.15), так, что с конца вектора поворот от к кажется против хода часовой стрелки. Модуль вектора равен

, (3.35)

где h₁ – кратчайшее расстояние от точки до линии действия вектора углового ускорения в данный момент времени (рис. 3.15).

Вектор осестремительного ускорения (рис. 3.15) перпендикулярен плоскости, в которой лежат векторы и , и направлен от точки М по перпендикуляру, проведенному из нее на мгновенную ось вращения тела. Модуль вектора , учитывая (3.32) и то, что , равен

. (3.36)

Ускорение точки тела, вращающегося вокруг неподвижной точки, равно геометрической сумме векторов вращательного и осестремительного ускорений.

Модуль ускорения

. (3.37)

Следует отметить, что формула Ривальса (3.33) аналогична формуле ускорения точки тела, вращающегося вокруг неподвижной оси. Но там векторы и перпендикулярны ( ) в отличие от формулы Ривальса.

В о п р о с ы для с а м о к о н т р о л я

1. Определение вращательного движения твердого тела вокруг неподвижной точки.

2. Какими параметрами определяется положение твердого тела, одна из точек которого неподвижна?

3. Какие параметры (так называемые корабельные углы), предложены А.Н. Крыловым для определения движения корабельных носителей на волнении?

4. Что принято за начало неподвижной системы координат, относительно которой определяется положение (движение) корабельного носителя и связанной с ним подвижной системы координат (рис. 3.1 и рис. 3.2)?

5. Формулы преобразования координат от связанной с кораблем системы координат к неподвижной системе координат.

6. Поворотные матрицы. Как определяется их структура?

7. В каких случаях рекомендуется использование углов Эйлера?

8. Какие параметры приняты за углы Эйлера. Какие оси называются осями прецессии, нутации, ротации (собственного вращения)?

9. Почему ось нутации называется линией узлов или замечательной осью.

10. Определение мгновенной оси вращения твердого тела с одной неподвижной точкой и каковы уравнения угловой скорости вращения в неподвижной и подвижной системах осей декартовых координат?

11. Уравнение мгновенной угловой скорости, выраженное как геометрическая сумма трех составляющих: угловых скоростей прецессии, нутации, ротации (и линии их действия).

12. Как определяется модуль, линия действия и направление углового ускорения тела при сферическом движении?

13. Почему направления векторов углового ускорения и угловой скорости тела при сферическом движении не совпадают?

14. Определение скоростей точек тела при сферическом движении.

15. Модули, линии действия и направления составляющих ускорения точки тела при сферическом движении.

16. Почему линии действия и направления векторов скорости точки и ее вращательного ускорения при сферическом движении тела не совпадают?

17. Какой частный случай вращения твердого тела , имеющего одну неподвижную точку, называется регулярной прецессией?

4. Расчетная работа № 1

Вращение твердого тела (корабельного на волнении или сухопутного на грунте носителя) вокруг неподвижной точки (регулярная прецессия)

Схемы конструкций и исходные данные

Определить: угол нутации , угловую скорость нутации , прецессии , ротации и мгновенную угловую скорость , угловое ускорение твердого тела; скорости и ускорения точек А, В, С подвижного конуса 1, катящегося без скольжения по неподвижному конусу 2 (рис. 4.1).

Задача сформулирована отдельно для каждого варианта, чертежи к задачам помещены на рис.4.1 (по последней цифре шифра (ПЦШ) выбирается номер схемы от 0 до 9), необходимые числовые данные, соответствующие (предпоследней цифре шифра (ПрЦШ) приведены в табл. 4.1. Во всех вариантах задачи (рис. 4.1) рассматривается регулярная прецессия твердого тела.

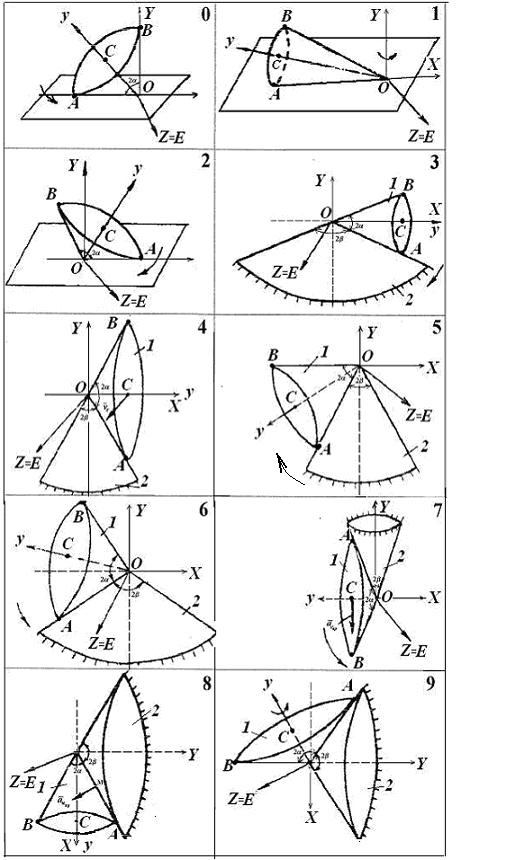
Рис. 4.1. Схемы к расчетной работе №1

Т а б л и ц а 4.1

Данные (ПрЦШ)=0		Последняя цифра шифра (ПЦШ)
		0	1	2	3	4	5	6	7	8	9
h	м	0,12	0,4	0,2	0,18	0,1	-	0,2	0,12	0,12	-
R		-	0,8	-	-	-	0,3	-	-	-	0,18
2	град	90	-	120	60	120	60	120	120	60	120
2		-	-	-	120	60	60	120	60	120	120
vc	м /с	-	2	-	-	0,2	-	-	-	-	-
a1	м/с2				0,36	-	-	-		0,48
n	об/мин	60	-	120	-	-	30/	-	-	-	30
t	с	-	-	-	-	-	-	2	-	-	-
Данные (ПрЦШ)=1		Последняя цифра шифра (ПЦШ)
		0	1	2	3	4	5	6	7	8	9
h	м	0,12		0,4	0,16	0,15	-	0,3	0,16	0,16	-
R		-	0,5	-	-	-	0,25	-	-	-	0,24
2	град	60	-	120	60	90	60	150	120	60	150
2		-	-	-	90	60	45	120	90	150	120
vc	м /с	-		-	-	0,45	-	-	-	-	-
a1	м/с2		-	-	0,32	-	-	-		0,72
n	об/мин	30	-	90	-	-	60/	-	-	-	60
t	с	-	-	-	-	-	-	4	-	-	-
Данные (ПрЦШ)=2		Последняя цифра шифра (ПЦШ)
		0	1	2	3	4	5	6	7	8	9
h	м	0,1	0,5	0,3	0,15	0,2	-	0,4	0,2	0,2	-
R		-	1,0	-	-	-	0,2	-	-	-	0,3
2	град	60	-	150	45	120	45	120	90	45	150
2		-	-	-	120	90	45	150	90	150	150
vc	м /с	-	1	-	-	0,8	-	-	-	-	-
a1	м/с2		-	-	0,3	-	-	-		0,8
n	об/мин	30/	-	60	-	-	90/	-	-	-	90
t	с	-	-	-	-	-	-	3	-	-	-

Варианты 0, 2. Прямой круговой конус с углом 2 при вершине катится без скольжения по неподвижной плоскости, делая n оборотов в минуту вокруг вертикальной оси OY в направлении, указанном стрелкой. Высота конуса OC = h.

Вариант 1. Прямой круговой конус катится без скольжения по неподвижной горизонтальной плоскости в направлении, указанном стрелкой. Высота конуса ОC = h, радиус основания равен R. Движение конуса происходит так, что скорость центра основания постоянна и равна v_C.

Варианты 3…9. Конус 1 с углом 2 при вершине катится без скольжения по неподвижному конусу 2 с углом 2 при вершине в направлении, указанном стрелкой. Высота конуса OC = h.

Движение конуса 1 происходит так:

• вар. 3  осестремительное ускорение центра С основания конуса при его вращении вокруг вертикальной оси OY постоянно и равно а₁;

• вар. 4  скорость точки С центра основания конуса постоянна и равна v_C , ↑↑ OZ в данный момент времени;

• вар. 5  подвижный конус 1 обегает неподвижный конус 2, совершая n оборотов в минуту, радиус основания конуса 1 равен R;

• вар. 6  подвижный конус 1 совершает за время t один оборот вокруг вертикальной оси против часовой стрелки;

• вар. 7  вращательное ускорение центра С основания конуса ;

• вар. 8  ускорение точки М конуса 1, лежащей на середине его образующей, равно , причем ;

• вар. 9 подвижный конус 1 совершает n оборотов в минуту вокруг своей оси симметрии Оy.