2.8. Последовательность действий при использовании уравнений Лагранжа II рода для решения задач о движении голономных систем

1. Определить число степеней свободы системы и выбрать наиболее удобные обобщенные координаты.

2. Вычислить кинетическую энергию системы в ее абсолютном движении и выразить эту энергию через обобщенные координаты и обобщенные скорости .

Напомним формулы кинетических энергий в абсолютном движении:

• для материальной точки ;

• для системы материальных точек ;

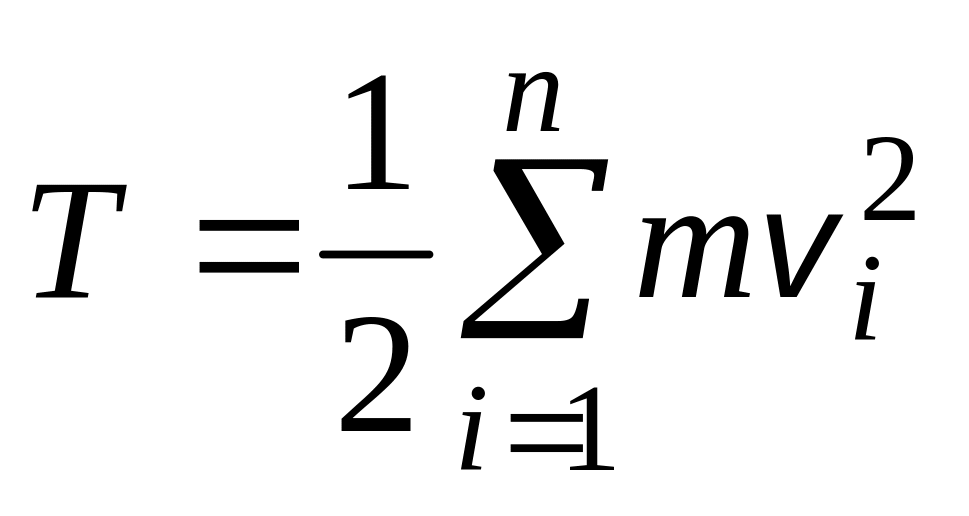• для твердого тела:

– при поступательном движении ;

– при вращении вокруг неподвижной оси l ;

– при плоскопараллельном движении

;

– при вращении вокруг неподвижной точки ;

– в общем случае движения твердого тела

.

3. Вычислить производные от кинетической энергии, входящие в левую часть уравнений Лагранжа.

4. Определить обобщенные силы, соответствующие выбранным обобщенным координатам (так как каждой обобщенной координате соответствует обобщенная сила, то число обобщенных сил механической системы равно числу обобщенных координат, причем размерность каждой из обобщенных сил соответствует размерности соответствующей обобщенной координаты).

5. Подставить все вычисленные величины в уравнения Лагранжа.

Пример 2.14. Механическая система (рис. 2.13) состоит из однородного круглого цилиндра 1 массой m₁ и радиусом r, однородного стержня 2 длиной l и массой m₂, к которому в точках А и В шарнирно прикреплены ползуны 3 и 4 массами m₃ и m₄, а также двух пружин с коэффициентами жесткости С₁ и С₂. Цилиндр без скольжения катится по горизонтальной плоскости. К нему приложена пара сил с моментом М₁(t).

Пренебрегая сопротивлением качению цилиндра 1, трением в шарнирах и направляющих, а также массой пружин, составить дифференциальные уравнения движения системы.

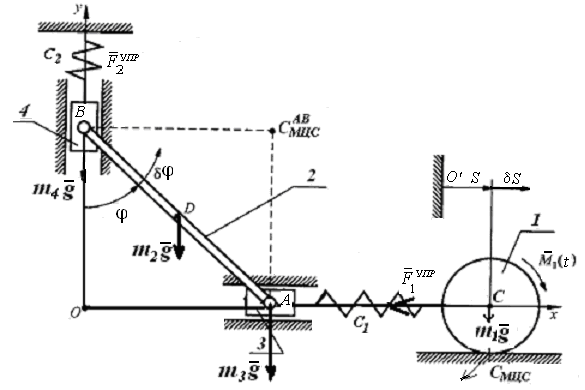
Рис. 2.13

Решение. Система имеет две степени свободы. В качестве обобщенных координат выберем перемещение q₁ = s центра масс С цилиндра 1 и угол q₂ =  поворота стержня 2 (против хода часовой стрелки). Полагаем, что при s = 0 и  = 0 пружины не деформированы.

Уравнения Лагранжа второго рода для данной системы имеют вид

. (2.27)

Кинетическая энергия системы складывается из кинетических энергий: цилиндра 1 и стержня 2, совершающих плоское движение; ползунов 3 и 4, совершающих поступательное движение: T = Т₁+ Т₂ + Т₃ + Т₄ .

Кинетическая энергия цилиндра 1 . Так как .

Кинетическая энергия стержня 2 . Ско-рость центра масс стержня , где – мгно-

венный центр скоростей (МЦС) стержня 2. Принимая во внимание, что получаем .

Ползуны движутся поступательно и, следовательно,

;

.

Таким образом, кинетическая энергия системы, выраженная через обобщенные координаты и обобщенные скорости, равна

.

Вычисляем производные от кинетической энергии системы:

– по q₁ = s

– по q₂ =  ;

;

.

Для нахождения обобщенных сил и , соответствующих обобщенным координатам, воспользуемся выражением виртуальной работы сил (2.15):

. (2.15а)

Эта формула позволяет вычислять обобщенные силы последовательно, учитывая, что обобщенные координаты, а значит, и их вариации не зависят друг от друга. Поэтому системе можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются.

1. При ,

, (2.28)

где , а выражение в квадратных скобках в (2.28) перед вариацией есть обобщенная сила

. (2.29)

2. При ,

(2.30)

где

Выражение в квадратных скобках в уравнении виртуальной работы (2.30) перед вариацией есть обобщенная сила

.(2.31)

Подставляя значения производных от кинетической энергии и выражения для обобщенных сил (2.29) и (2.31) в (2.27), получаем дифференциальные уравнения движения системы:

по q₁ = s ;

по q₂ =  

.

В о п р о с ы д л я с а м о к о н т р о л я

1. Определение свободной и несвободной механической системы.

2. Несвободное движение системы. Аналитическое выражение связей и их классификация. Примеры.

3. Для какого уравнения связей излагается дальнейшая теория составления уравнений движения несвободной механической системы?

4. Определение возможных и виртуальных перемещений. Примеры. Направление виртуального перемещения.

5. Определение обобщенных координат механической системы.

6. Чему равно число независимых координат, однозначно определяющих положение механической системы, состоящей из n материальных точек?

7. Чему равно число степеней свободы механической системы, на которую наложены h уравнений ограничений?

8. Имеют ли обобщенные координаты начало отсчета и направление?

9. Приведите примеры, доказывающие, что обобщенные координаты – независимые друг от друга параметры (неявные функции времени.).

10. Несвободное движение системы материальных точек или тел.

11. Определение виртуальной работы. Идеальные связи. Пример.

12. От каких сил вычисляется виртуальная работа?

13. Четыре формулы определения виртуальной работы (по аналогии с формулами элементарной работы).

14. Выражение виртуальной работы системы через обобщенные силы.

15. Определение размерности обобщенной силы для различных обобщенных координат.

16. Способы нахождения обобщенных сил.

17. Определение обобщенной силы через силовую функцию в случае действия на систему потенциальных сил.

18. Вид уравнений Лагранжа второго рода? Чему равно число этих уравнений для данной механической системы?

19. Формулы кинетических энергий для точки, системы точек, твердого тела в зависимости от вида его движения (при поступательном, вращательном вокруг неподвижной оси и точки, при плоском движении и в общем случае его движения).

20. Вид уравнений Лагранжа второго рода для механической системы, на которую действуют только потенциальные силы.

21. Последовательность действий при использовании уравнений Лагранжа второго рода для решения задач о движении голономных систем с несколькими степенями свободы.