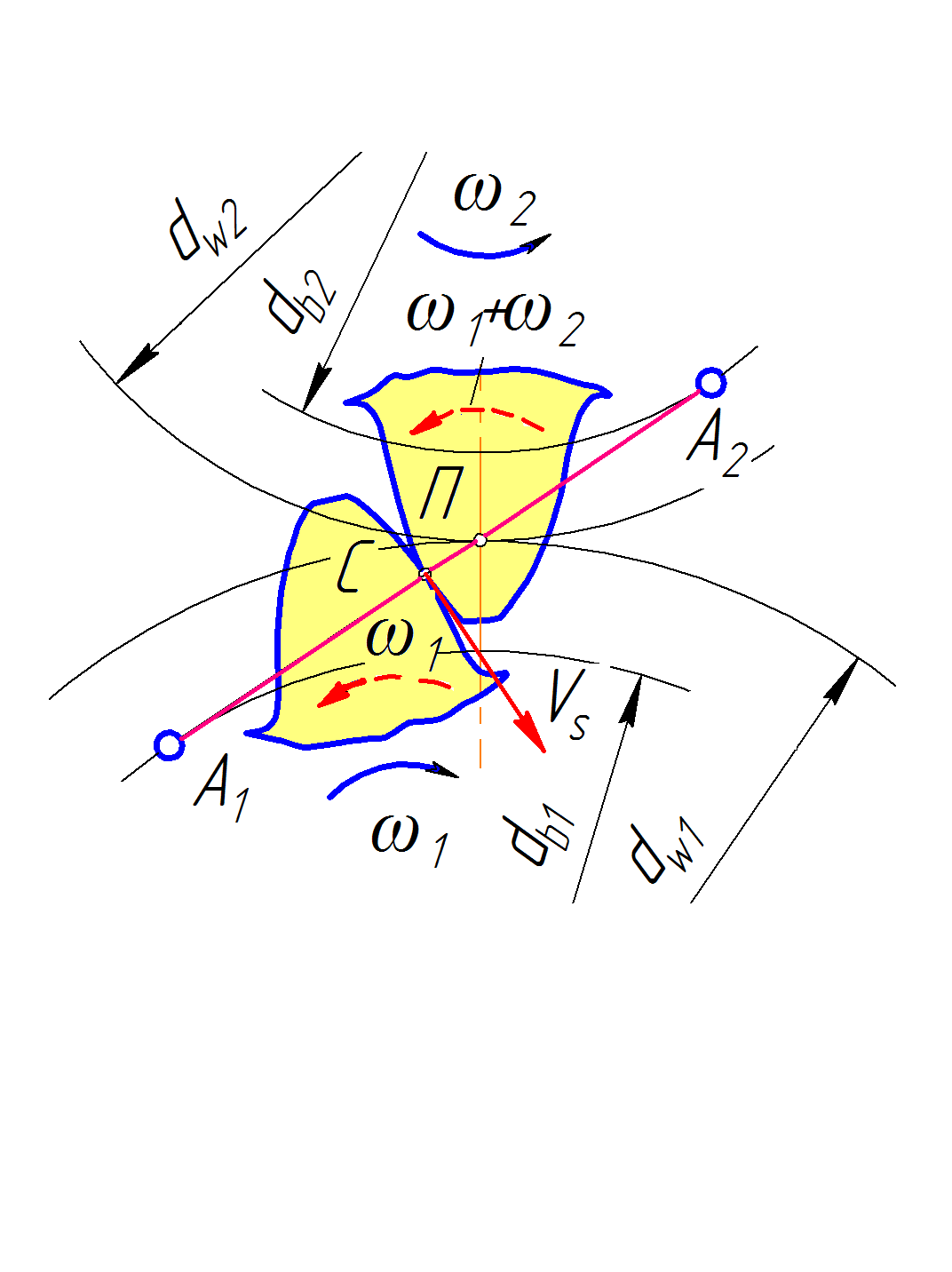
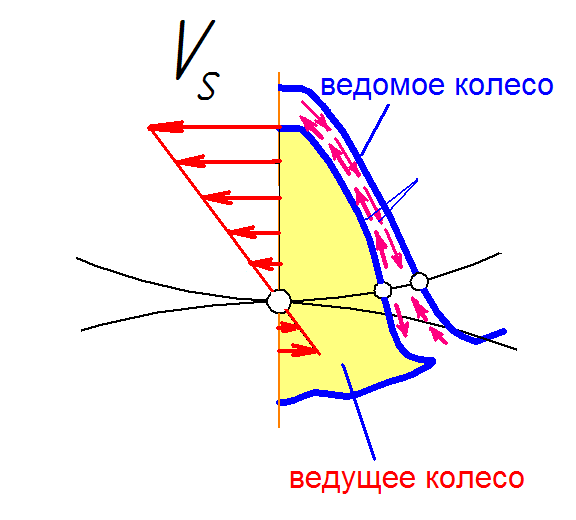
15 Скольжение и трение в зацеплении при работе зубчатых передач.
Скорость скольжения Vs как относительную скорость можно определить, используя известное правило механики. Сообщим всей системе угловую скорость w1 с обратным знаком. При этом шестерня останавливается, а колесо проворачивается вокруг полюса зацепления П, как мгновенного центра, с угловой скоростью, равной (w1+w2). Скорость относительного движения в точке С
Vs=e(w1+w2)
Скорость скольжения пропорциональна расстоянию е точки контакта от полюса. В полюсе она равна нулю, а при переходе через полюс меняется знак. Скольжение сопровождается трением, а трение является причиной потерь в зацеплении и износа зубьев.(стр 118 иванов)
Скольжение и трение в зацеплении
e = ПС
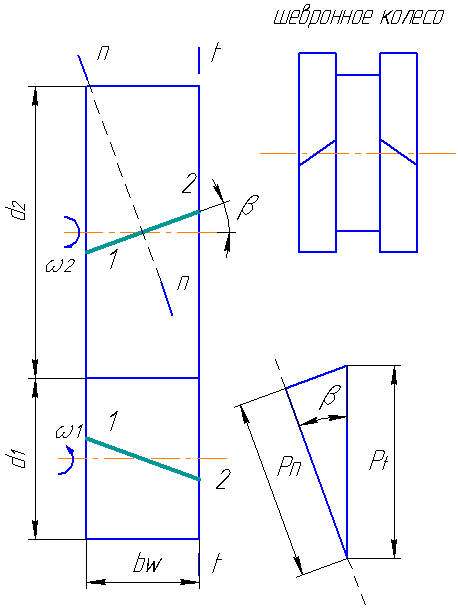
16 Особенности геометрии косозубых цилиндрических передач.
Косозубые цилиндрические передачи осуществляют передачу вращательного движения между параллельными осями . В общем случае для косозубых передач рассматривают окружные и нормальные шаги и соответствующие модули. Окружность делительная: шаг Pi –это расстояние между одноименными профилями соседних зубьев, изменяется по дуге делительной окружности зубчатого колеса.
Нормальный шаг Pн – кратчайшее расстояние по делительному цилиндру между одноименными поверхностями двух смежных зубьев. Pn=Pi* cos B; где B-угол наклона линии зубьев по делительному цилиндру; соответственно нормальный модуль m=mi*cos B
Угол профиля зуба(эвольвенты) –альфа=20 градусов. Делительный диаметр d=mi*z=mn*z/cos B. С увеличением угла B повышается прочность косозубых передач, способные передавать большие нагрузки, меньший уровень шума.
Особенности геометрии косозубых цилиндрических передач
Угол наклона зубьев β в косозубых цилиндрических передачах:
β = 8...20°.
Для шевронных колес:
β = 25...40°.
В раздвоенных косозубых ступенях редукторов:
β >= 30°.
В соосных передачах с косозубыми колесами
(при заданном aw):
β=arccos[mn(z1+z2)/2aw],
где mn – нормальный модуль (мм)
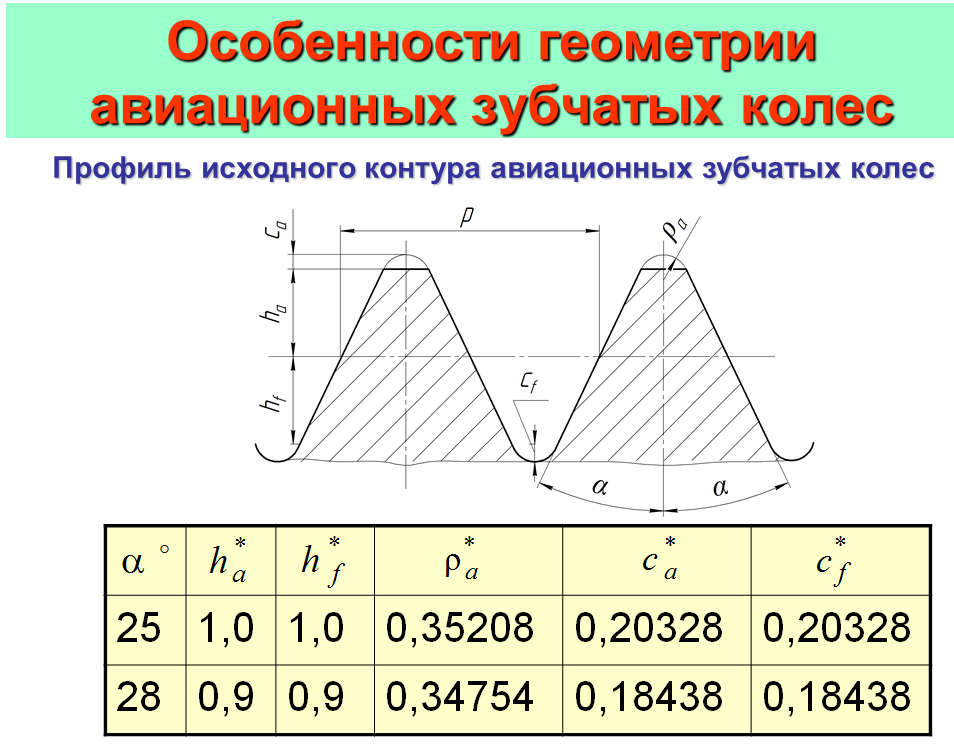
17 Особенности геометрии авиационных зубчатых колес
Обычно угол профиля альфа=20 градусов; из-за больших нагрузок и повышенных требований угол альфа=25,28 и больше т.е. зуб получается мощнее и его характеристики по механическим свойствам намного выше, чем для наиболее широко применяемых 20 градусов. Профиль исходного контура авиационных зубчатых колес
17
18
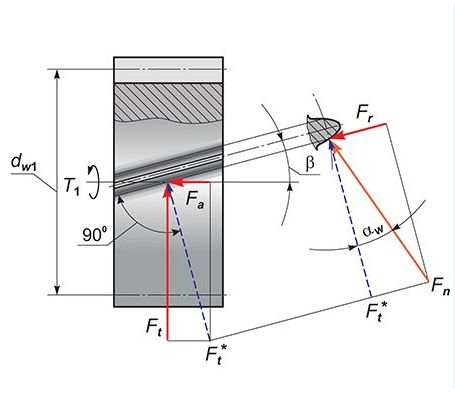
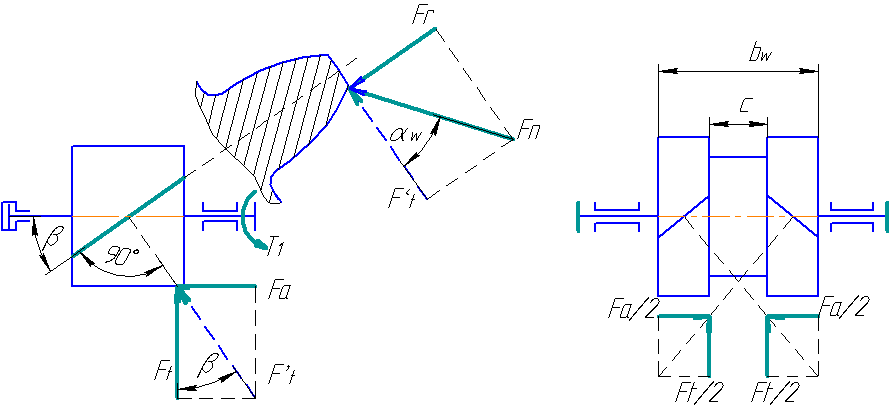
Силы в зацеплении косозубой и шевронной передачах
Окружная сила
Ft = 2T1/d1
Осевая сила
Fа = Ft tgβ
Радиальная сила
Fr = F't tgαw=Ft tgαw/cosβ
Fn = F't/cos αw = Ft / (cosαw cosβ )
18 Силы в зацеплении косозубой и шевронной передачах.
У косозубых колес зубья располагаются не по образующей делительного цилиндра, а составляет некоторый угол B. Оси колес при этом остаются параллельными. Для нарезания косых зубьев используюь инструмент такого же профиля(контура) как и для нарезания прямых зубьев.
Параметры косого зуба изменяются в зависимости от угла B:
В косозубой передаче нормальную силу Fн раскладывают на три составляющие: окружную силу, осевую силу, радиальную силу.
Наличие в зацеплении осевых сил, которые нагружают опоры валов(подшипники) являются недостатком косозубых цилиндрических колес.
Этот недостаток отсутствует в шевронных передачах, в которой осевые силы уравновешиваются в самом колесе. Тк косые зубья имеют противоположное направление.