2. Способ допусков одного квалитета точности.

При таком способе предполагают, что все составляющие цепь размеры могут быть выполнены по одному квалитету точности, а допуски составляющих размеров зависят от их номинального значения. Требуемая степень квалитета точности определяется следующим образом.

Величина допуска каждого размера равна Т=аi, где i – единица допуска. Для размеров от 1 до 500 мм , где А_iср – средний размер для интервала диаметров по ГОСТ ( ), к которому относится данный линейный размер. Тогда

где а_i – число единиц допуска, содержащееся в допуске данного i-го размера звена.

Далее в соответствии с уравнением (5.4) можно написать

откуда

; (5.11)

где ТА_ - в мкм; А_iср – в мм.

По а_ср выбирают ближайший квалитет точности.

Число единиц допуска а_ср, полученное по формуле (5.11) в общем случае не будет равняться какой-либо из величин а, определяющих квалитет точности по ГОСТ 25347-82. Поэтому, выбрав ближайший квалитет точности и найдя по таблицам ГОСТ величины допусков составляющих размеров в соответствии с их номинальной величиной, корректируют их значения, учитывая конструктивно-эксплуатационные требования и возможность применения такого процесса изготовления, экономическая точность которого близка к требуемой точности размеров. Допуски для охватывающих размеров рекомендуется определять, как для основного отверстия, а для охватываемых – как для основного вала.

После нахождения величин допусков А₁, А₂, … , А_m-1 по заданным величинам В.О.А_ и Н.О.А_ определяются величины и знак верхних и нижних отклонений составляющих размеров max, чтобы они удовлетворяли уравнениям (5.7) и (5.8).

Решение второй задачи (обратной) способом назначения допусков одного квалитета точности является более обоснованным по сравнению со способом равных допусков. Примеры на практических занятиях.

Основными преимуществами метода полной взаимозаменяемости является:

1. Наибольшая простота достижения требуемой точности замыкающего звена, т.к. построение размерной цепи сводится к простому соединению всех составляющих ее звеньев. Например, использование этого метода при сборке превращает сборку в простое соединение деталей;

2. Простота нормирования процесса во времени, при помощи которых достигаются требуемая точность замыкающего размера;

3. Относительная простота механизации и автоматизации технологических процессов;

4. Возможность кооперирования различных цехов и отдельных заводов.

Эти преимущества способствуют широкому использованию метода полной взаимозаменяемости. Однако, он может оказаться экономически целесообразным лишь для машин не высокой точности или для цепей, цепей состоящих из малого количества звеньев. В других случаях, особенно при расчете точности негеометрических параметров, допуски могут быть чрезмерно жесткими и технологически трудновыполняемыми; при установлении же технологически выполняемых допусков может получиться, что

В таких случаях допуски рассчитываются другими методами.

3. Теоретико – вероятносный метод расчета

РАЗМЕРНЫХ ЦЕПЕЙ

Сущность метода заключается в том, что требуемая точность замыкающего звена размерной цепи достигается не во всех размерных цепях, а у подавляющего их большинства.

При выводе формул (2) – (8) и др. для расчета размерных цепей методом max - min предполагалось, что в процессе обработки или сборки возможно одновременное сочетание наибольших увеличивающих и наименьших уменьшающих размеров или обратное их сочетание. Оба случая наихудшие в смысле получения точности замыкающего звена, но они мало, вероятны, т.к. отклонение размеров в основном группируется около середины поля допуска. На этом положении и основан теоретико-вероятностный метод расчета размерных цепей.

Отличие этого метода от метода полной взаимозаменяемости в установлении больших по величине допусков на составляющие звенья, что делает изготовление деталей и эксплуатацию машин, которым принадлежат эти звенья, более экономичным. При этом идут на риск получения небольшого процента случаев выхода погрешности замыкающего звена размерной цепи за пределы установленного допуска.

Первая задача. Получая, что погрешности составляющих и замыкающего размера подчиняются закону нормального распределения, а границы их, вероятно, рассеяны, (6) совпадают с границами полей допусков, можно принять:

или

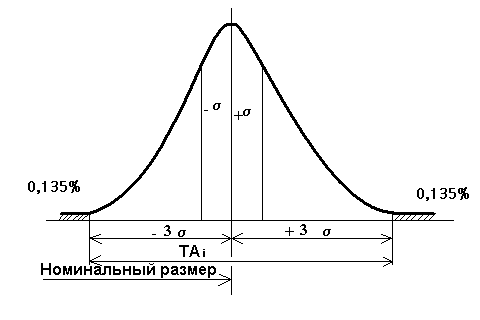Рис.5.3. Поле рассеяния для нормального распределения

При этом у 27% изделий размеры замыкающих звеньев могут выходить за пределы поля допуска.

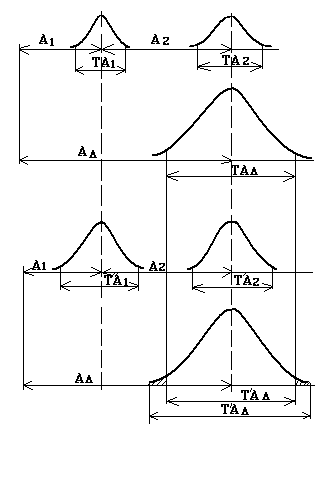Проиллюстрируем на примере 3-х звенной размерной цепи, допуски на составляющие звенья равны т.е. А₁=А₂ и для обоих составляющих звеньев принят закон нормального распределения (кривая Гаусса).

При нормальном распределении:

При решении методом полной взаимозаменяемости:

.

Для нашего случая:

.

При решении этой же задачи методом неполной взаимозаменяемости допуски обоих составляющих звеньев устанавливаются большими, т.е.

или

и допуск замыкающего звена в этом случае будет больше чем необходимо, на величину

это может вызвать появление некоторой части изделий, погрешности замыкающего звена которых будет выходить за пределы требуемого допуска А_ замыкающего звена. Величина этой части изделий определяется отношением суммы 2-х заштрихованных площадок ко всей площади кривой рассеяния замыкающего звена (F₁/F). Поэтому уравнение (5.4) решения размерной цепи запишется так:

(5.12)

где k – коэффициент относительного рассеивания, характеризующий степень отличия распределения погрешностей i-го параметра по сравнению с распределением по закону Гаусса; При нормальном распределении k=1 при законе равной вероятности для (рис.1) k=1,73, при законе Симпсона k= 1,22.

 - относительное среднее квадратичное отклонение от центра группирования случайной величины

;

 - поле рассеяния, =6:

для закона Гаусса ;

для закона равной вероятности ;

для закона Симпсона .

Коэффициенты k_ и _ вводится только для размерных цепей, в которых число составляющих звеньев менее пяти.

Поскольку величина (поле рассеяния) допуска ТА_ распределяется симметрично относительного среднего размера А_, то полученную величину допуска по формуле (12) расписывают симметрично В.О. с (+); и Н.О. с (-) относительно среднего размера подсчитанного по методу полной взаимозаменяемости.

Пример.

А₁=30⁺¹, А₂ = 20_+0,1^+0,3, А₃=20_-0,1^+0,2, А₀=80_-0,1

При решении по 1 методу:

EA_=

Н.О.=-0,7 мм, А_=10_-0,7, А_ср=9,65 мм

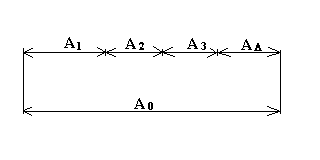
При решении по методу неполной взаимозаменяемости

Таким образом, замыкающее звено будет иметь допуск 0,43 мм, а не 0,7 мм как при методе полной взаимозаменяемости, т.е. он будет выдерживаться более точным, и в результате этого у 27% размерных цепей размеры замыкающего звена могут выходить за указанные пределы.

Вторая задача. При решении обратной задачи – допуски составляющих звеньев цепи при заданном допуске исходного размера можно рассчитать четырьмя способами:

1. При способе равных допусков принимают, что величины ТА_i и k_i для всех составляющих размеров одинаковы. По заданной величине ТА_определяют_срА_i, удовлетворяющее уравнению (5.12).

Уравнение для определения _срА_i , определяется

откуда

(5.13)

Если коэффициент k_i не одинаковый для всех составляющих размеров, то знаменатель в формуле (5.13) имеет вид .

2. При способе назначения допусков одного квалитета точности расчет, в общем, аналогичен решению второй задачи методом полной взаимозаменяемости, но формула (11) примет другой вид:

(5.14)

3. Способ пробных расчетов заключается в том, что допуски на составляющие размеры назначают экономически целесообразным для условий предстоящего вида производства с учетом конструктивных требований, опыта эксплуатации имеющихся подобных механизмов и проверенных для данного производства значений коэффициентов k_i и _i.

Для повышения точности, надежности, долговечности и обеспечения функциональной взаимозаменяемости машин допуски и предельные размеры исходного и составляющих размеров, применяемые в существующих машинах, следует корректировать в сторону ужесточения с целью создания запаса на износ. После такого расчета размерной цепи проверяют выполнимость равенства (5.12). Если равенство не выполняется, то допуски, а иногда и номинальные значения составляющих размеров вновь корректируют.

4. Способ равного влияния применяют при решении плоскостных и пространственных размерных цепей. Он основан на том, что допускаемое отклонение каждого составляющего размера должно вызывать одинаковое изменение исходного размера.