Метод решения размерных цепей
ОБЕСПЕЧИВАЮЩИЙ ПОЛНУЮ
ВЗАИМОЗАМЕНЯЕМОСТЬ
Чтобы обеспечить полную взаимозаменяемость, размерная цепь решается по методу max и min, при котором допуск замыкающего размера определяется арифметическим сложением допусков составляющих размеров.
Различают две задачи:
Первая задача. У детали вначале обрабатывается плоскость 1, затем по настройке от этой базы – плоскость 2, в размер А2=28 0.14 мм и плоскость 3 в размер А1= 60 0.2 мм.
В технологической линейной размерной цепи размер А является замыкающим; его величина зависит от действительных размеров А1(увеличивающего) и А2 (уменьшающего):
.
В общем случае при n увеличивающих и p уменьшающих размерах уравнение размерной цепи можно представить в виде
(5.1)
По уравнению (5.1) определяется номинальный размер замыкающего звена линейной размерной цепи через номинальные размеры составляющих звеньев этой цепи. Оно будет справедливо и в том случае, когда вместо номинальных взяты значения соответствующих действительных размеров размерной цепи.
Составляющие размеры могут изменяться в установленных допусками пределах. При сочетании наибольших увеличивающих и наименьших уменьшающих составляющих размеров А будет иметь наибольшее значение, а при сочетании наименьших увеличивающих и наибольших уменьшающих составляющих размеров – наименьшее значение т.е.
(5.2)
(5.3)
Учитывая, что разность между max и min предельными размерами есть допуск, получаемый:
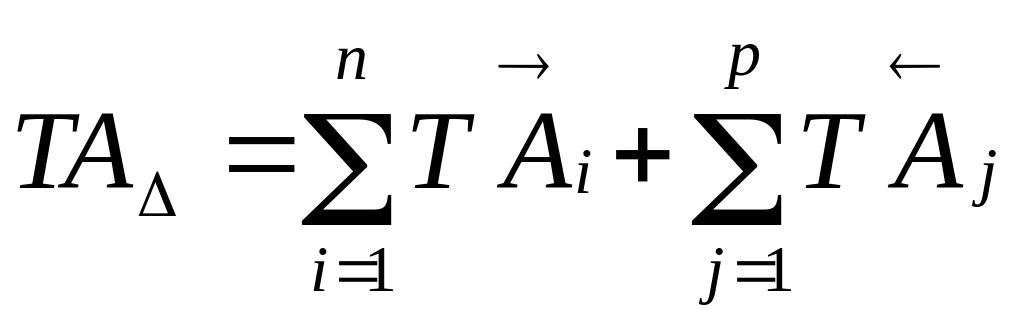
Если принять общее количество звеньев в цепи равным m, а общее количество составляющих звеньев равным m-1=n+p, то
(5.4)
Пример: при А1=0,40 мм и А2=0,28 мм допуск замыкающего размера А = 0,4+ 0,28 = 0,68 мм.
Равенство (4) показывает также, что в каждый момент времени погрешность замыкающего звена равна алгебраической сумме погрешностей всех составляющих звеньев цепи. Поэтому, чтобы обеспечить наименьшую погрешность замыкающего звена, размерная цепь должна состоять из возможно меньшего числа звеньев, т.е. необходимо при конструировании изделий соблюдать принцип кратчайшей цепи. Кроме того, порядок обработки и сборки деталей нужно строить (если это возможно) таким образом, чтобы замыкающим размером являлся менее ответственный размер, (его погрешность будет наибольшей).
Определение предельных отклонений замыкающего размера
или
(5.5)
В то же время
(5.6)
Вычитая из уравнения (5) уравнение (6), получаем
В общем случае это уравнение можно представить в виде
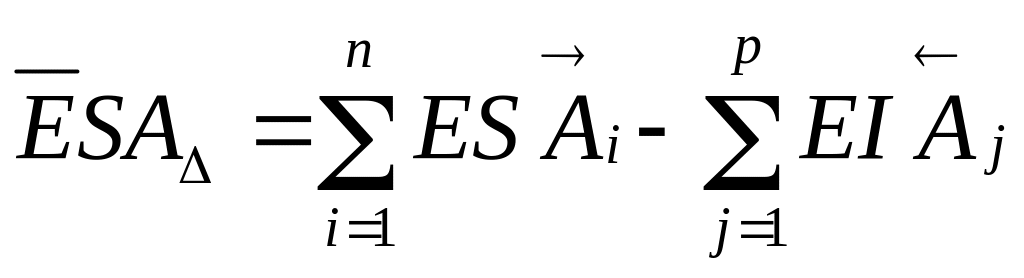(5.7)
аналогично
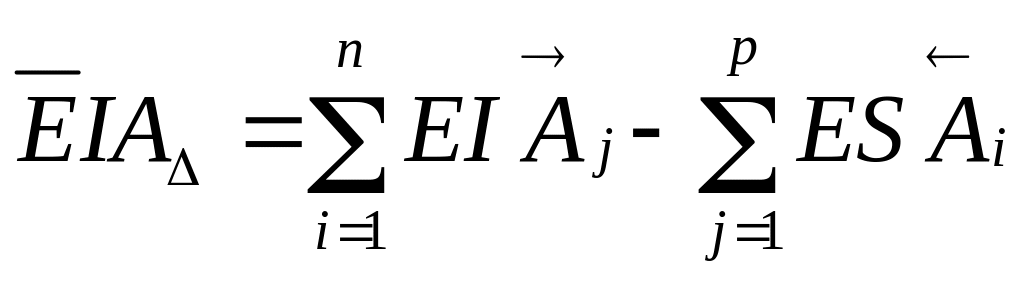(5.8)
Пользуясь уравнением (7) и (8), определяем предельные значения замыкающего размера для нашего примера
таким образом А=320,34 А=Анаиб-Анаим=32,34-31,66=0,68 мм. Как видим, допуск замыкающего размера равен сумме допусков составляющих размеров, т.е. уравнение (4) удовлетворено.
На основании уравнения (4) напишем формулу для определения допуска любого составляющего размера при условии, что известны допуски и предельные отклонения остальных размеров цепи, включая и замыкающий размер:
(5.9)
где суммируется допуски всех составляющих звеньев, кроме звена С.
Вторая задача. Такая задача встречается на практике чаще. При заданной точности сборки (величине допуска исходного размера) – обеспечить выполнение машиной ее служебного назначения. Точность составляющих размеров должна быть такой, чтобы гарантировалась заданная точность исходного (функционального) размера. Эту задачу можно решить двумя способами:
1.Способ равных допусков.
Применяют, если составляющие размеры являются величинами одного порядка (например, входят в один интервал диаметров) и могут быть выполнено с примерно одинаковой экономической точностью. В этом случае можно условно принять
Тогда из уравнения (4) получим
;
откуда
(5.10)
Полученный средний допуск ТсрАi корректируется для некоторых составляющих размеров в зависимости от их величины, конструктивных требований и технологических трудностей изготовления, но так чтобы удовлетворялось уравнение (4). При этом, как правило, надо использовать только стандартные поля допусков, желательно предпочтительного применения.
Способ равных допусков прост, но достаточно точен, т.к. корректировка допусков составляющих размеров произвольна.