43. Пример астатической системы автоматического управления с принципом управления по отклонению.

У астатических в установившемся режиме ошибка регулирования равна нулю. Отличительной чертой астатических систем является наличие оператора свободного Р в знаменателе передаточной функции системы (т.е. наличие в ней интегрирующих звеньев). Степень оператора называется порядком астатизма. Есть еще одна отличительная черта астатических систем: каждая единица степени астатизма сдвигает ЛФЧХ системы вниз на 90°.

В астатических системах обязательно есть идеальное интегрирующее звено.

Звенья, для которых можно задать статическую характеристику в виде жесткой функциональной зависимости выходной величины от входной, называются статическими. Если такая связь отсутствует и каждому значению входной величины соответствует множество значений выходной величины, то такое звено называется астатическим. Изображать его статическую характеристику бессмысленно. Примером астатического звена может служить двигатель, входной величиной которого является напряжение U, а выходной - угол поворота вала , величина которого при U = const может принимать любые значения. Выходная величина астатического звена даже в установившемся режиме является функцией времени.

Если на управляемый процесс действует возмущение f, то важное значение имеет статическая характеристика САУ в форме y = F(f) при yo = const. Возможны два характерных вида этих характеристик (рис.19). В соответствии с тем, какая из двух характеристик свойственна для данной САУ, различают статическое и астатическое регулирование.

В некоторых случаях статическая ошибка недопустима, тогда переходят к астатическому регулированию, при котором регулируемая величина в установившемся режиме принимает точно требуемое значение независимо от величины возмущающего фактора. Статическая характеристика астатической САУ не имеет наклона (рис.19в). Возможные неточности относятся к погрешностям конкретной системы и не являются закономерными.

19

Для того, чтобы получить астатическое регулирование, необходимо в регулятор включить астатическое звено, например ИД, между ЧЭ и УО (рис.23).

Если уровень воды понизится, то поплавок переместит движок потенциометра на величину L, за счет этого появится разность потенциалов 0 и ИД начнет поднимать заслонку до тех пор, пока не уменьшится до нуля, а это возможно только при y = yo . При поднятии уровня воды разность потенциалов сменит знак, и двигатель будет вращаться в противоположную сторону, опуская заслонку.

Достоинства и недостатки статического и астатического регулирования: статические регуляторы обладают статической ошибкой; астатические регуляторы статической ошибки не имеют, но они более инерционны, сложны конструктивно и более дороги.

Лекция Андриевской

С

татическими называются такие САУ, у которых при постоянном задающем воздействии ошибка в установившемся режиме стремится к некоторой постоянной неравной нулю.

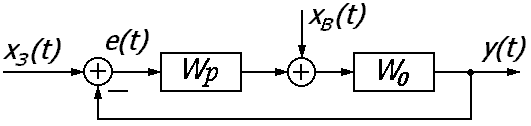
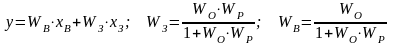
Часто при расчете систем передаточные функции и уравнение динамики записывают не для управляемой величины х, а для сигнала ошибки

,

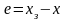который также может рассматриваться как сумма двух составляющих:

,

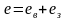где е_в, е_з – составляющие сигнала ошибки, обусловленные изменениями соответственно возмущающего и задающего воздействий.

Для каждой составляющей сигнала ошибки можно записать передаточные функции, связывающие эти составляющие с соответствующими внешними воздействиями.

Передаточная функция системы по задающему воздействию равна

,

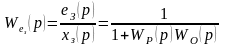
а

передаточная функция по возмущающему воздействию

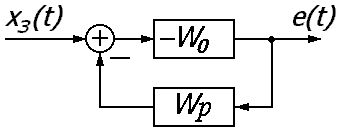
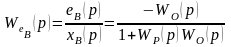
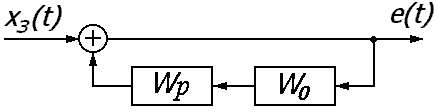
Уравнение динамики системы, записанное для сигнала ошибки, будет иметь вид

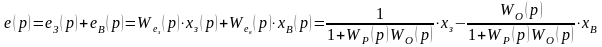
Рассмотрим для примера следующий случай: пусть .

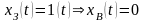Тогда ошибка будет зависеть только от задающего воздействия

.

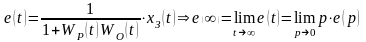Пусть для нашего случая 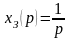, тогда

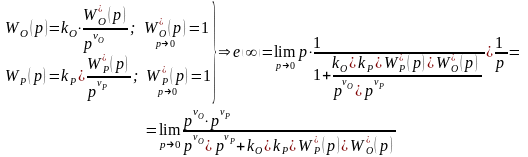
Здесь _О является порядком астатизма у объекта, а _Р – у регулятора, причем если _О0 и _Р0, то ошибка будет равна нулю.

Если регулятор или объект содержат интегрирующие звенья, то ошибка в установившемся режиме будет равна нулю, следовательно, система является астатической.

Статической будет та САУ, в которой ни регулятор, ни объект не будут содержать интегрирующих звеньев. Кроме того, статическая САУ – это САУ имеющая нулевой порядок астатизма.