
М инистерство
образования и науки Российской Федерации
инистерство
образования и науки Российской Федерации
ФГБОУ ВПО
«СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
ХТФЗДО
Кафедра системотехники.
Курсовая работа
(СТ220700.030)
Руководитель
Лутошкина Н В
___________
(подпись)
____«_____»________2012г.
(оценка, дата)
Разработал:
Студент группы 2207с
Зыков А В
___________
(подпись)
«_____»_________
(дата)
Сибирский государственный технологический университет
Кафедра системотехники
Задание на курсовую работу по дискретной математике
Студент Вензель Александр Андреевич
Факультет АИТ Группа 2101-11с
Тема курсовой работы: «Исследование методов решения задач дискретной математики»
Требуется:
Задание 1
Изобразить на диаграммах Эйлера-Венна. При необходимости выражение упростить, используя тождества алгебры множеств.
Задание 2
Доказать с помощью основных тождеств и показать на диаграммах Эйлера-Венна.
Задание 4
Схематично изобразить геометрическое место точек прямого произведения множеств.
Задание 6
Дано отношение.
a) Построить примеры пар отношения.
b) Построить графическое представление.
c) Выяснить свойства отношения: рефлексивность, симметричность, транзитивность, антисимметричность.
2. Теория графов
Задание 1. Ориентированный граф
Охарактеризовать граф.
Назвать специальные вершины и рёбра.
Рассчитать полустепени вершин.
Выписать матрицы смежности, инцидентности, достижимости, связности.
Выписать цикл, цепь, простой цикл, простую цепь.
Задание 2. Неориентированный граф
Начертить граф по матрице длин дуг. Самостоятельно обозначить ребра.
Охарактеризовать граф.
Назвать специальные вершины и рёбра.
Рассчитать степени вершин.
Выписать матрицы смежности, инцидентности, достижимости, связности.
Выписать цикл, цепь, простой цикл, простую цепь.
Рассчитать ОД и МОД.
Красноярск, 2013

Содержание
2. Теория графов 2
1Множества и отношения 6
Задание 1 6
Задание 2 7
Задание 3 8
Задание 4 8
Задание 5 8
Задание 6 9
Задание 7 10
2. Теория графов 11
Задание 1. Ориентированный граф 11
Задание 2. Неориентированный граф 13
Реферат
Курсовая работа представляет собой решение задачи
1Множества и отношения Задание 1
Изобразить на диаграммах Эйлера-Венна. При необходимости выражение упростить, используя тождества алгебры множеств.
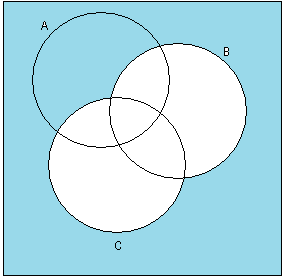
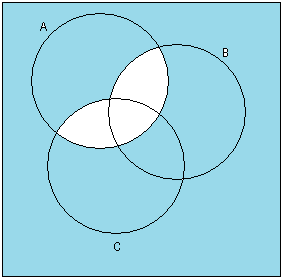


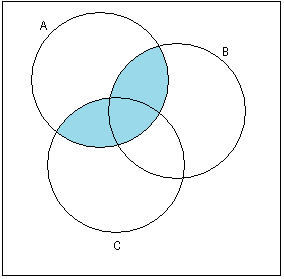
2)

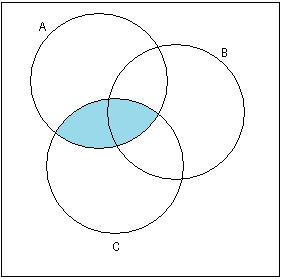
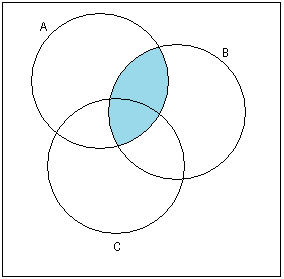
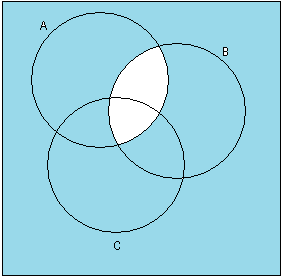

 ̚(A
̚(A B)
B)
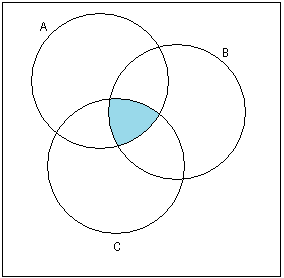
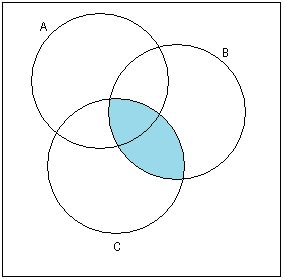
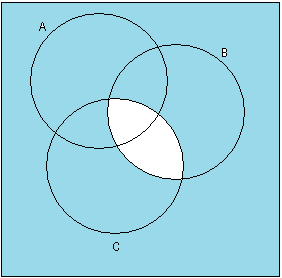
(
)\̚
(A B
B ̚ (B
̚ (B
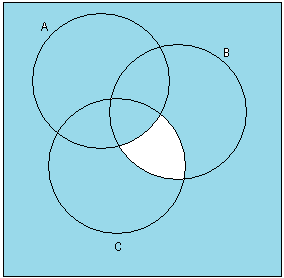
Задание 2
Доказать
с помощью основных тождеств и показать
на диаграммах Эйлера-Венна.

Решение:

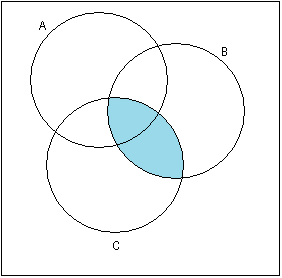
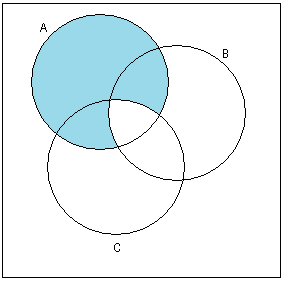
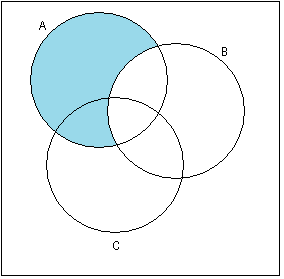
(B
)
 A\B
A\B
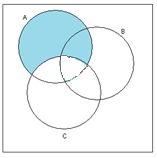
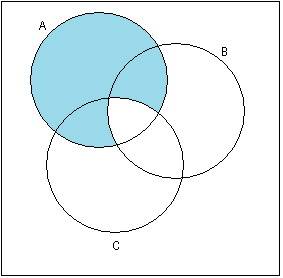
A\C
(A\B)
 (A\C)
(A\C)
Задание 3
Доказать по определению:

Решение:
A -
множество А включено в множество B
или совпадает с ним.
-
множество А включено в множество B
или совпадает с ним.
Пусть
< x,y>
 (
A
(
A B) * ( C
D)
B) * ( C
D)
 x
(A
B), y
( C
D )
x
A , x
B, y
C , y
x
(A
B), y
( C
D )
x
A , x
B, y
C , y x
A, y
C
x
B, y
x
A, y
C
x
B, y

<x,y> (A * C) <x,y> (B * D) <x,y> (A*C) (B*D)
<x,y> (A*C) (B*D) <x,y> (A*C) <x,y> (B*D) x A, y C x B,y D
x
A
x
B, y y
D
x
(A
B),y
(C
D)
<x,y>
(A
B)*(C
D)
y
D
x
(A
B),y
(C
D)
<x,y>
(A
B)*(C
D)
(A B)*(C D)выполнимо тогда и только тогда,когда (A*C) (B*D)

