2.6. Основные критериальные уравнения для расчетов коэффициентов теплоотдачи и теплопередачи

В инженерной практике при проведении тепловых и гидравлических расчетов широко используются критерии подобия физических процессов, которые лежат в основе теории подобия.

Теория подобия – учение о подобных явлениях. У подобных явлений должны быть подобны поля всех физических величин, характеризующих эти явления. Например, подобия в процессах теплоотдачи можно достигнуть при равенстве скоростей (или критерия, характеризующего режим течения – критерия Рейнольдса Re), вязкости, плотности, теплопроводности.

Исследование подобных явлений позволяет изучать различные (вплоть до аварийных) режимы теплообмена на модели в меньшем масштабе. При этом устанавливают закономерности и взаимосвязи параметров в виде эмпирических зависимостей. Полученные и многократно проверенные эмпирические зависимости широко используются в типовых тепловых расчетах. Основные критерии подобия, используемые в тепловых расчетах, приводятся ниже.

2.6.1. Критерий Re выражает отношение сил инерции скоростного напора к силам вязкого трения:

, (8)

где - кинематическая вязкость среды;

l – геометрический параметр, характеризующий проходное сечение, обычно диаметр канала или его эквивалентный диаметр.

В случае конвекции в межтрубном пространстве при омывании пучков труб или стержней определяется эквивалентный диаметр по формуле:

, (9)

Где: П – смоченный периметр, [м];

S – проходное или живое сечение канала, [м²].

2.6.2. Критерий Прандтля характеризует отношение вязкости и температуропроводности веществ, учитывая пристеночные явления, и определяется по формуле:

; (10)

2.6.3. Критерий Нуссельта считается безразмерным коэффициентом теплоотдачи и определяется по формуле:

, (11)

Где:  - коэффициент теплоотдачи, [Вт/(м²^оК)];

l – геометрический параметр, [м];

 - коэффициент теплопроводности среды, [Вт/(м^оК)].

Критерий Nu определяется в зависимости от вида конвекции: вынужденной или естественной и зависит от соответствующих значений критериев Re, Gr, Pr.

Эмпирические формулы устанавливаются для определенного диапазона этих критериев подобия.

В случае вынужденной конвекции общий вид эмпирической критериальной зависимости имеет вид:

₍₁₂₎

Где: - коэффициент, учитывающий относительный шаг между трубами;

- коэффициент, учитывающий условия омывания труб теплоносителем; относительный шаг труб (он всегда больше единицы);

– шаг между трубами;

– диаметр трубы в пучке.

и являются табличными величинами, зависящими от произведения GrPr, и определяются по справочникам.

Различают плотные пучки труб, где 1,1<Х<1,4 и разреженные пучки труб, где Х>1,4. Например, плотные пучки – трубчатка парогенераторов АЭС (Х = 1,2), разреженные пучки – конвективные шахты котлов X > 3,0.

В случае естественной конвекции критерий Nu определяется через критерии Gr в общем виде:

₍₁₃₎

2.6.4. Критерий Грасгофа Gr – отношение подъемной силы, возникающей в результате теплового расширения жидкости к силам тяжести, он определяется по формуле:

, (14)

Где:  - температурный коэффициент объемного расширения жидкости;

t – перепад температур между стенкой и средой;

 - кинематическая вязкость;

l – геометрический параметр; в случае горизонтального расположения труб он равен диаметру, при вертикальном расположении труб он равен их высоте;

Коэффициент теплоотдачи в общем виде определяется по формуле через критерий Нуссельта:

, (15)

Теплофизические характеристики, входящие в критерии подобия, определяются по средней расчетной температуре теплоносителя:

(16)

Например, значение критерия Nu при течении воды в прямых гладких трубах и каналах при l/d > 40 и турбулентном режиме течения (Re > 10⁴) определяется по формуле:

₍₁₇₎

При поперечном омывании пучков гладких труб при Re > 6000 значение числа Нуссельта в общем случае определяется по формулам для коридорного расположения прямых труб:

; (18)

Для шахматного расположения прямых труб при или пучков спиральных труб справедлива следующая формула:

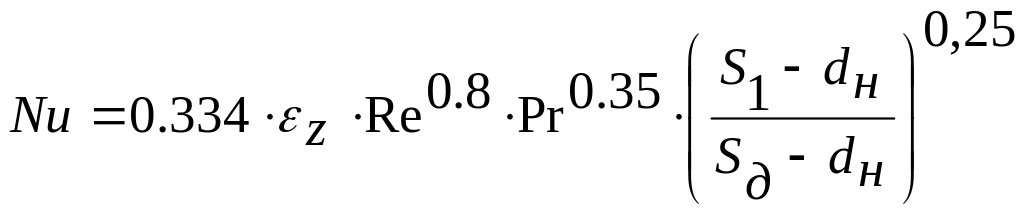; (19)

Для коридорного расположения таких же труб при

. (20)

Здесь: – поправка на число рядов труб в продольном направлении, определяемая по номограммам рис. 3;

– диагональный шаг, определяемый по формуле (21).

, (21)

Рис. 3 Коэффициент для учета количества рядов в трубном пучке

Где: S₁ – поперечный шаг труб в пучке;

S₂ – продольный (по направлению обтекающего потока) шаг труб в пучке.

Число Нуссельта в этом случае находится по формуле:

. (22)

Значение для пучков из круглых труб определяется по таблице 1.

Табл. 1

Угол атаки	90º	80º	70º	60º	50º	40º	30º	20º	10º
Коэффициент	1	1	0,98	0,94	0,88	0,78	0,67	0,52	0,42

Для пучков, в которых одна часть труб омывается продольным, а другая поперечным потоком теплоносителя, коэффициенты теплоотдачи в межтрубном пространстве вычисляются отдельно для каждой части пучка (для средних значений температуры) и усредняются пропорционально поверхностям нагрева обеих частей:

. (23)

Если поверхность нагрева поперечно обтекаемого участка составляет более 85% всей поверхности нагрева, то весь пучок рассчитывается как поперечно обтекаемый.

При ψ = 90^о÷60º характер омывания можно считать поперечным,

при ψ = 10^о÷0º – продольным.

На участках, где происходит пленочная конденсация теплоносителя среднее численное значение для пленки, стекающей по поверхности вертикальных труб, равно:

, (24)

а для горизонтальных труб:

, (25)

где – количество конденсата, натекающего на единицу длины рассматриваемой трубы от выше расположенных труб;

– средняя плотность теплового потока.

Режим течения пленки при – чисто ламинарный, при – волновой, при – переходный, при – турбулентный.

Значение величины приведены в таблице 2.

Табл. 2.

, ºС	50	100	150	200	250	300
, Вт/м	1295	632	382	260	198	126

Средний коэффициент теплоотдачи при конденсации водяного пара на вертикальных трубах, когда и , рассчитывается по формуле:

, (26)

где – поправка на волновой характер стекания конденсата:

при ; при ;

– поправка, учитывающая зависимость физических свойств конденсата от температуры:

,

и – коэффициенты теплопроводности среды у стенки и в состоянии насыщения, [Вт/м·^oК];

и – коэффициенты динамической вязкости среды у стенки и в состоянии насыщения, [Па·с];

– поправка на шероховатость и загрязнение, принимается по таблице 3;

– определяющий геометрический размер, равен полной длине трубы, в случае отсутствия перегородок, [м];

– температурный напор пар - стенка:

,

– средняя температура стенки,

– температура насыщения.

Табл. 3.

Характеристики поверхности
Чистые латунные трубы	1,0
Чистые трубы из нержавеющей стали	1,0
Цельнотянутые трубы из углеродистой стали	0,8
Сильно окисленная шероховатая поверхность из углеродистой стали	0,75

Значение коэффициента А определяется по формуле:

, (27)

Средняя скорость пара вычисляется по формуле:

, (28)

где и – соответственно скорость пара на входе в пучок труб и выходе из него.

Если скорость пара на выходе из пучка , то .

Средний коэффициент теплоотдачи при конденсации водяного пара на вертикальных трубах при и , рассчитывается по формуле:

, (29)

Значение коэффициента В определяется по формуле:

. (30)

Значение коэффициентов А и В в зависимости от температуры приведены в таблице 4.

Табл. 4.

Коэффи- циенты	Температура, ºС
	0	20	40	60	80	100	120	140	160	180	200
А	7001	8446	9680	10710	11590	12320	12780	13110	13290	13310	13170
В	8071	12676	17735	22969	28260	32796	37681	41170	44077	46287	47799

Теплопроводность материалов [Вт/(м·^оК)], используемых для изготовления поверхностей нагрева подогревателей приведена в таблице 5.

Табл. 5

Температура[ºС]	Латунь			Сталь
	Л-62	Л-68	ЛО70-	20	22К	15ХМ	08Х18Н10Т	08Х14Ф
0	105,8	100,0	105,8	–	–	–	–	–
100	119,8	107,0	109,3	50,7	49,4	44,4	16,3	24,7
200	137,2	112,8	110,5	48,6	47,7	–	17,6	26,0
300	152,4	121,0	114,0	46,0	45,6	41,4	18,8	26,4
400	168,6	127,9	116,3	42,3	43,5	–	21,4	–

Коэффициент теплопередачи для гладких толстостенных труб определяем по формуле:

, (31)

Где: и – коэффициенты теплоотдачи от теплоносителей со стороны наружной и внутренней поверхности труб соответственно, [Вт/(м²·^oК)];

– коэффициент теплопроводности материала стенки, [Вт/(м·^оК)];

и – наружный и внутренний диаметр труб, [м].

Для определения поверхности теплообмена при конструктивном расчете следует применять формулу:

(32)