Обработка результатов косвенных измерений
При косвенных
измерениях значение измеряемой величины,
например, ускорение
находят по функциональной зависимости
через другие непосредственно измеряемые
величины (в нашем примере силу
и массу
).
Пусть величина
измеряется косвенно через величины
,
для которых по результатам прямых
измерений определены их средние значения
,
случайные погрешности
с одинаковой вероятностью и систематические
погрешности
.
По этим данным следует произвести
оценку среднего значения
,
случайной
и систематической
погрешностей.
Оценка результата измерений
Оценку результата измерений можно произвести двояко. Во-первых, как значение функции z при значении аргументов, равным средним значениям:
.
(5)
Во-вторых, можно
провести для каждого из
измерений расчет значений
,
,…,
,
найти среднее арифметическое по формуле
(1) и принять его за оценку результата.
Выбирается тот способ, который удобнее.
Оценка систематической погрешности
Между систематической
погрешностью измерения величины
и дифференциалом
существует аналогия – и та и другая
величины являются малым приращением
функции. Для функции
полный дифференциал
.
Так как знак погрешностей измерения величин неизвестен, то систематическая погрешность оценивается как среднее квадратичное по формуле
,
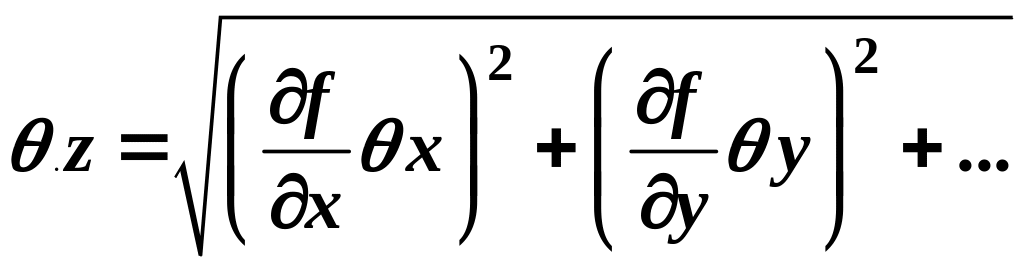(6)
где
,
… – частные производные, определяемые
при средних значениях
,
,
…;
– систематические погрешности величин
.
Если функция сложная, ее вначале логарифмируют, а затем дифференцируют, т.е. формула (6) принимает вид
.
(7)
Оценка случайной погрешности
1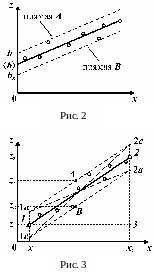
способ. Если величину
измерить столько раз, сколько раз
проведены измерения величин
,
то по результатам
можно оценить случайную погрешность
по формуле (2), как при прямых измерениях.
2 способ. Если
функция
линейная (или ее можно свести к
линейной), то можно наиболее просто
определить случайную погрешность
графически.
Пусть по
экспериментальным точкам проведена
прямая (рис. 2) и нужно оценить случайную
погрешность величины
.
Проведем параллельно экспериментальной
прямой по обе стороны две линии на равном
расстоянии, так, чтобы большинство точек
(95 %) оказалось внутри. Тогда интервал
можно трактовать как интервал, равный
– четырем среднеквадратичным погрешностям,
внутрь которого попадает не менее 95 %
измерений:
.
Тогда, случайная
погрешность
по формуле (2)
.
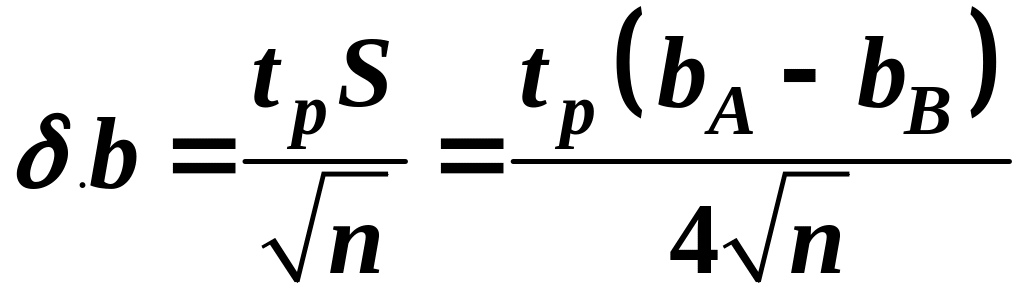(8)
Для оценки случайной
погрешности углового коэффициента,
среднее значение которого из треугольника
123 (рис. 3)
,
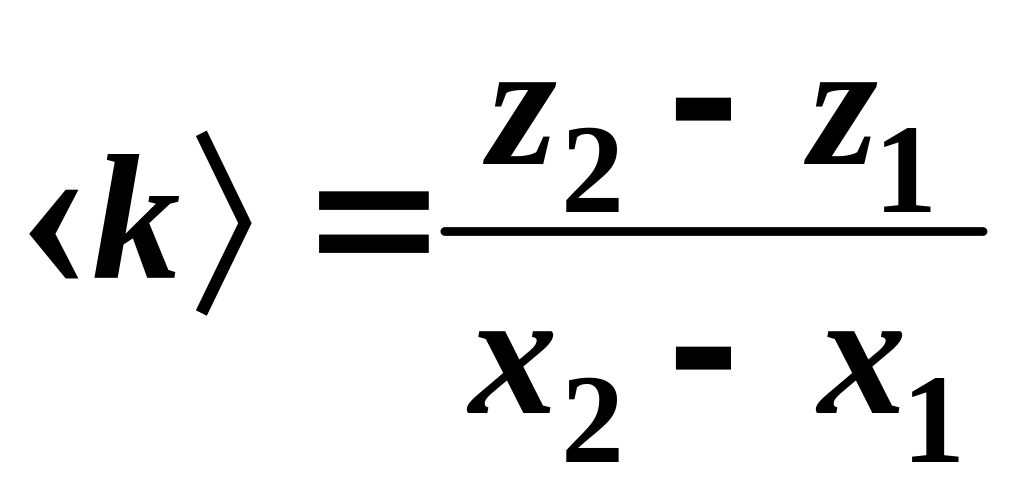также проводят параллельно экспериментальной
прямой две линии так, чтобы большинство
(95 %) точек оказалось внутри (рис. 3).
Крайние точки 1а–2а, 1с–2с
соединяют крест-накрест.
Это – экспериментальные прямые, проведенные под максимально и минимально возможными углами. Их угловые коэффициенты:
(9)
Их можно трактовать
как наибольшее и наименьшее значения
углового коэффициента, отличающегося
от среднего на
:
Тогда случайная погрешность аналогично
(7)
.
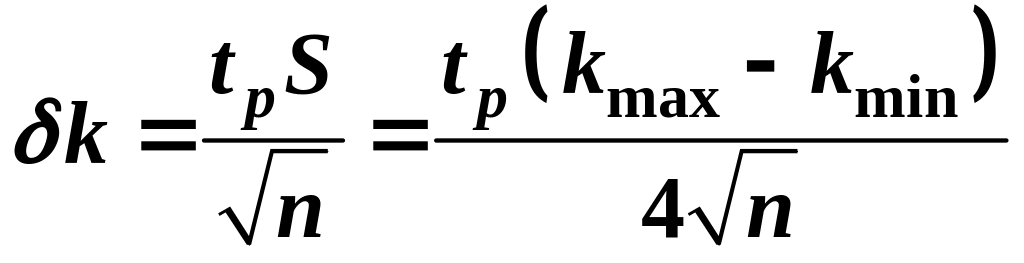(10)
Можно еще упростить оценочную формулу, если подставить в (10) выражение (9), то получим
,
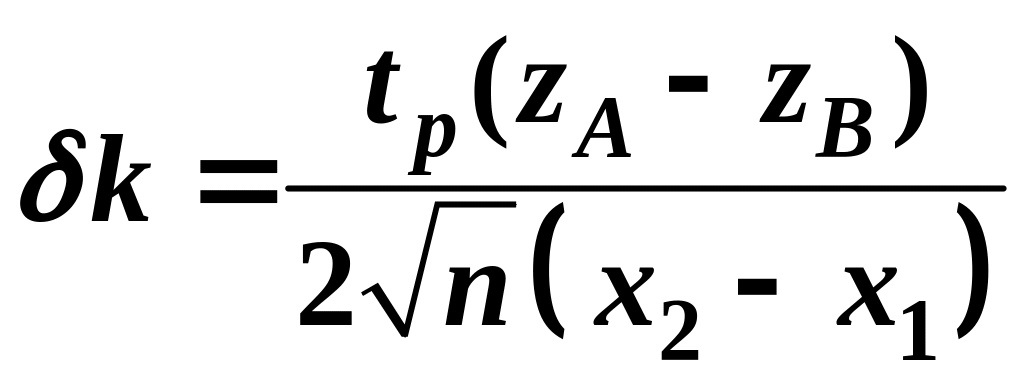(11)
где
– расстояние между вспомогательными
прямыми А и В.
3 способ. Пользуются аналогией между дифференциалом функции и случайной погрешностью так же, как в случае оценки систематической погрешности (см. формулу (7)):
.
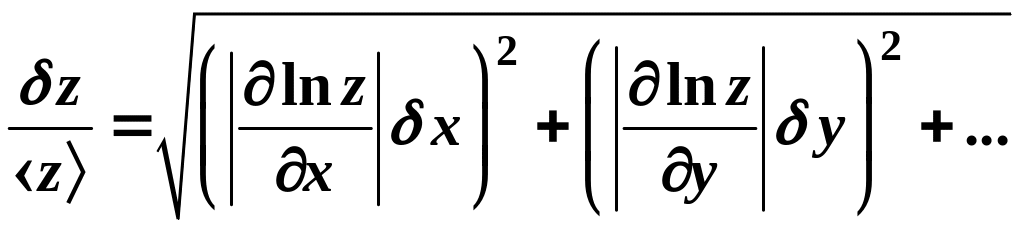(12)
Оценка суммарной погрешности и запись окончательного результата производятся так же, как и при прямых измерениях.
Из предложенных способов оценки случайной погрешности выбирают наиболее удобный. Доверительная вероятность графического способа = 0,95.