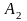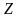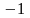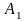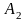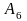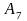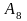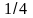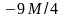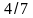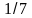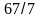Дополнительный материал к решению корневой задачи

Краткая теория и примеры решения симплекс-методом

(см. также [1, гл 3], [3, раздел 4.9])

Симплекс-метод является наиболее распространенным универсальным методом.

Идея метода состоит в последовательном продвижении по базисам опорных планов задачи, т.е. в последовательном улучшении планов задачи по заданному критерию до тех пор, пока не будет получено оптимальное решение.

Необходимо предварительно выполнить следующие шаги:

• привести математическую модель к каноническому виду;

• определить начальное базисное решение задачи;

• заполнить начальную симплекс-таблицу по начальному базисному решению, для чего ввести в нее:

- коэффициенты C_j при переменных в целевой функции;

- векторы (переменные), которые входят в текущий базис;

- значения базисных переменных в столбец ;

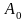- элементы a_ij , матрицы условий задачи 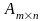(столбцы ); Оценки 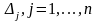, соответствующие векторам , для начальной таблицы вычисляются по формуле:

,

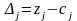Коэффициенты критерия 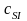при базисных переменных проставляются в левый столбец таблицы соответственно векторам базиса.

Значение целевой функции при текущем базисе:

- заносится в последнюю строку столбца .

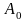Пример 1. Модель задачи

Приведем заданную модель к каноническому виду, введя дополнительные переменные и , превращающие неравенства в равенства:

.

Начальное базисное решение построим на переменных , соответственно образует начальный базис, а 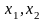становятся небазисными переменными; =(10,20) -вектор ограничений.

Заполняем симплекс-таблицу, соответствующую начальному базисному решению:

Табл. 0				0	1		1		0		0
i		Баз
1	0	A3
2	0	A4
			0		-1	-1		0		0
			0		0	0		0		0

min

Элементы строки рассчитаны по формулам:

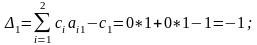
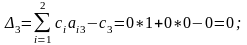
Для базисных переменных оценки всегда равны нулю.

Значение критерия для данного начального решения равно

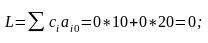
Так как имеются , признак оптимальности в начальном плане не выполняется. Приступаем к улучшению плана.

ПЕРВАЯ ИТЕРАЦИЯ

В базис будем вводить вектор , которому соответствует минимальное значение , то есть этот столбец становится направляющим. Направляющая строка определяется по минимальному значению . Величина находится как результат деления элемента столбца A₀ на соответствующий положительный элемент направляющего столбца

.

Минимум достигается в строке с , которая становится направляющей, а из базиса будет выведен вектор .Таким образом, элемент 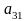, расположенный на пересечении направлющих столбца и строки будет направляющим (здесь индексы элемента соответствуют индексам векторов выходящего и входящего в базис).

Заполняем таблицу, соответствующую новому базисному решению.

Все элементы 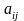таблицы определяются по следующему рекуррентному соотношению:

где -направляющий элемент, -номер итерации.

Из нижней части формулы следует, что элементы направляющей строки пересчитываются путем деления каждого ее элемента на направляющий. Верхняя часть формулы реализуется построением прямоугольника на элементе, новое значение которого хотим получить. Проектируя этот элемент на направляющую строку и направляющий столбец, получаем прямоугольник. В его вершинах находятся все 4 элемента, входящие в формулу (в вершине, противоположной вычисляемому элементу, всегда лежит направляющий элемент). После пересчета, называемого симплекс-преобразованием, получаем следующую таблицу

Табл. 1			0	1	1	0	0
i		Баз
1	1							----
2	0	A4
			10	0	-1	1	0
			10	1	0	1	0

min

Приведем пример расчета нескольких элементов табл.1:

Этой формуле соответствует прямоугольник, построенный на элементе 20 в табл.0, другие его вершины находятся на элементах 10, 1 и 1.

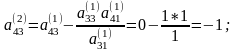
Заметим, что элементы базисных столбцов вычислять не надо, так как в них только один элемент равен 1, а остальные равны нулю.

Так как в строке оценок полученного нового плана имеется отрицательное значение , переходим ко второй итерации с целью последующего улучшения плана.

ВТОРАЯ ИТЕРАЦИЯ

Она проводится аналогично первой итерации. Результаты представлены в табл.2.

Табл. 2			0	1	1	0	0
i		Баз
1	1
2	1					-1/2	1/2
			15	0	0
			15	1	1

Поскольку все , то план, представленный в данной таблице, является оптимальным.

Ответ: ; ; ; ;

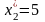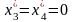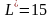Если система ограничений исходной модели представлена неравенствами вида 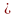либо равенствами, начальный опорный план не может быть найден так же просто, как в рассмотренном примере. В таких случаях начальный план строится с помощью искусственных переменных. Они вводятся в модель после приведения ее к каноническому виду в те условия, которые были неравенствами  или равенствами.

Пример 2. Найти максимум функции

;

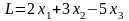при ограничениях:

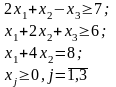
Приводим модель к каноническому виду введением дополнительных переменных x₄ и x_{5 в} первые два условия. Но они не могут быть базисными, так как при нулевых исходных переменных примут отрицательные значения. Поэтому начальное базисное решение строим на искусственных переменных 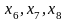. Такое решение удовлетворяет требованию неотрицательности переменных, но не обеспечивает выполнение условий задачи и, следовательно, является недопустимым.

Чтобы ускорить вывод искусственных переменных из решения (обращение в ноль), введем их в целевую функцию с большим отрицательным коэффициентом М (в задаче минимизации – с положительным М). Окончательно модель примет вид

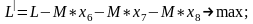
при ограничениях

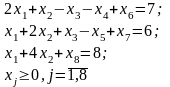
Начальному решению соответствует начальный базис, включающий векторы 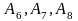. Теперь можно заполнить начальную таблицу и провести итерации симплекс-метода аналогично 1-му примеру.

Табл 0		0	2	3	-5	0	0	-M	-M	-M	
	Баз
-M		7	2	1	-1	-1	0	1	0	0	7
-M		6	1	2	1	0	-1	0	1	0	3
-M		8	1	4	0	0	0	0	0	1	2
		-21M	-4M -2	-7M -3	5	M	M	0	0	0

Элемент 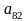=4 является направляющим.

Столбцы, соответствующие искусственным переменным, по мере вывода из базиса можно исключать из таблицы (если не требуется проводить двойственный или параметрический анализ).

В результате пересчета всех элементов получаем следующую таблицу.

Таблица 1		0	2	3	-5	0	0	-M	-M	
	Баз
-M		5		0	-1	-1	0	1	0	20/7
-M		2		0	1	0	-1	0	1	4
3		2		1	0	0	0	0	0	8
		-7M+6		0	5	M	M	0	0

В этой таблице направляющим является элемент = . На его основе получаем очередную симплекс-таблицу.

Таблица 2		0	2	3	-5	0	0	-M	
	Баз
2			1	0			0	0	--
-M			0	0			-1	1	4/9
3			0	1			0	0	9
		+	0	0	+	– -	M	0

После очередной итерации получаем табл.3.

Таблица 3		0	2	3	-5	0	0	
	Баз
2			1	0	0	–4/9		–
-5			0	0	1			2
3		1	0	1	0			11
		7	0	0	0

В табл.3 получено допустимое (все искусственные переменные равны нулю), но не оптимальное решение. Поэтому продолжим симплекс-преобразования, результаты которых представлены в табл.4 и 5.

Таблица 4		0	2	3	-5	0	0	
	Баз
2		4	1	0	2	0	–2	–
0		2	0	0	9/2	1		–
3		1	0	1	–1/2	0		2
		11	0	0	5/2	0

Таблица 5		0	2	3	-5	0	0
	Баз
2		8	1	4	0	0	0
0		9	0	7	1	1	0
0		2	0	2	–1	0	1
		16	0	5	5	0	0

В этой таблице нет отрицательных оценок, то есть выполнился признак оптимальности, и итерации завершились.

Примечание. При выполнении признака оптимальности следует проверить решение на наличие искусственных переменных. Если есть хотя бы одна положительная искусственная переменная, значит, получено недопустимое решение, что указывает на неразрешимость задачи из-за противоречивости условий. Если все искусственные переменные обнулились и выполнился признак оптимальности, то получено оптимальное решение.

В нашем случае все искусственные переменные вышли из решения (равны нулю) и, следовательно, получено оптимальное решение:

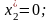
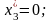
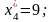
ЗАДАНИЯ НА КУРСОВУЮ РАБОТУ

Цель курсовой работы – закрепление и углубление знаний, полученных студентами в процессе изучения системного анализа и исследования операций, развитие навыков самостоятельной работы при решении конкретных оптимизационных задач, освоение и практическое применение пакета прикладных программ LINDO.

Каждому студенту выдается отдельная задача из класса задач исследования операций. Любая из задач, в конечном итоге, сводится к задаче линейного программирования, целочисленного программирования или квадратичного программирования. Для решения таких задач и предназначен пакет LINDO. В объеме, достаточном для выполнения курсовой работы, этот пакет описан в [15]. Получить доступ к пакету можно на кафедре или скачать демоверсию с сайта разработчика www.lindo.com (размерность решаемых задач ограничена). При выполнении курсовой работы обращайтесь к дополнительной литературе.

Конкретные задания и подробные методические указания по выполнению курсовой работы изложены в пособии

Гольдштейн А.Л. Методические рекомендации и варианты курсовой работы по дисциплине «Системный анализ и исследование операций», – Пермь: ЦНТИ, 2006. Пособие можно получить в библиотеке ЭТФ, количество экземпляров достаточное для всех студентов..