Метод потенциалов.

Данный метод еще называют модифицированным распределительным методом (МОДИ).

После того как найден исходный опорный план перевозок, каждому поставщику (каждой строке) ставится в соответствие некоторое число ( ), а каждому потребителю (каждому столбцу) – некоторое число . Числа и называют потенциалами соответственно поставщика и потребителя . Они выбираются так, чтобы в каждой базисной клетке их разность равнялась тарифу этой клетки, то есть из равенства - = .

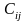Так как потенциалов m+n, а занятых (базисных) клеток m+n-1, то для определения значений и приходится решать систему из m+n-1 уравнений - = с m+n неизвестными. В этом случае одной из неизвестных можно присвоить произвольное значение, и тогда система будет иметь единственное решение, т. е. все остальные m+n-1 неизвестных определятся однозначно с точностью до постоянной величины. Потенциалы нужны для вычисления оценок, которые позволяют определять статус текущего плана. Оценки вычисляются только для небазисных (свободных) клеток по формуле 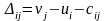(Для базисных клеток оценки заведомо равны нулю). План оптимален, если для всех небазисных переменных 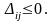Оценка показывают, как изменится критерий при перемещении по циклу пересчета единицы груза. Положительные оценки указывают на перспективность клеток, загрузка их приведет к улучшению плана. Для наиболее перспективной клетки строится замкнутый контур, называемый циклом пересчета. Все вершины цикла кроме исходной принадлежат базисным клеткам. Такой цикл может быть построен для любой небазисной (свободной) клетки единственным образом. Вершинам цикла приписываются чередующиеся знаки (свободной клетке приписывается положительный знак). Клетки с «плюсом» назовем четными, а с «минусом» – нечетными. В нечетных клетках цикла отыскивается наименьший груз, который и перемещается по клеткам цикла, т.е. прибавляется к клеткам со знаком плюс, включая свободную, и вычитается в клетках со знаком минус. На последующих итерациях оценки находятся не через потенциалы, а путем преобразования предыдущей матрицы оценок.

Когда среди оценок не окажется отрицательных, полученный план будет оптимальным.

Пример

Решить методом потенциалов транспортную задачу, представленную в следующей таблице:

Поставщик	Потребитель				Запасы груза
	B1	B2	B3	B4
A1	3	8	2	1	10
A2	1	4	3	5	30
A3	7	2	1	6	40
Потребность в грузе	20	5	30	25	80

Решение. Задача сбалансирована. Опорный план перевозок найдем, например, по правилу северо-западного угла. В полученном плане (см. ниже) число занятых клеток r =m+n-1=3+4-1=6, то есть план не вырожден. Значение критерия в этом начальном плане:

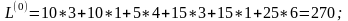
Поставщик	Потребитель				Запасы груза
	B1	B2	B3	B4
A 1	3 10 -	8	2	1 +	10
A2	1 10 +	4 5	3 15 -	5	30
A3	7	2	1 15 +	6 25 -	40
Потреб-ность	20	5	30	25	=80

Определяем потенциалы и :

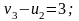
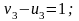
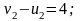
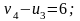
Полагая, например, 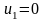, находим остальные потенциалы:

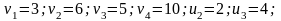
Вычисляем 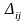для свободных клеток:

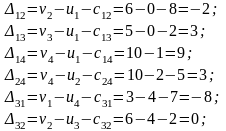
Матрица оценок для начального плана перевозок:

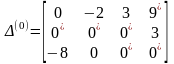
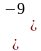
Строим цикл на той клетке, где самая большая оценка. Это клетка (1,4). Находим

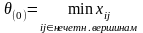и перемещаем по циклу ₀, добавляя к четным вершинам и вычитая из нечетных.

Так для построенного цикла

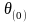=min(10,15,25)=10.

Переместив это значение по циклу, получаем новый план перевозок:

Новое значение критерия:

первая итерация улучшила критерий на 90 единиц.

Преобразуя матрицу ⁽⁰⁾ по решению x⁽¹⁾, находим новую матрицу оценок

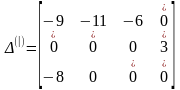
(В ⁽⁰⁾ помечались элементы, соответствующие базисным в решении x⁽¹⁾).

Рассмотрим, как можно преобразовать матрицу ^(k) в матрицу ^(k+1) на основе нового решения .

Находим максимальный элемент матрицы ^(k)

max .

В матрице отмечаем элементы, соответствующие базисным в новом решении (на рисунке помечены символом *), максимальную оценку отмечаем особо. Далее строим цепочку выделения. Она строится с особо отмеченного элемента, который соединяют с отмеченными в этой строке. Затем отмеченные элементы, попавшие в цепочку, соединяют с отмеченными в их столбцах. Далее снова проводим соединение по строкам , и так до тех пор, пока не оборвутся все ветви.

Элементы, попавшие в цепочку выделения, выделяют строку и столбец за исключением особо отмеченного элемента, он выделяет только строку. К выделенным столбцам прибавляем, а из выделенных строк вычитаем , в результате получаем матрицу ^{( k+1)} .

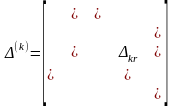
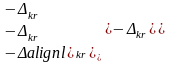
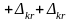
Можно вместо построения цепочки выделения вычеркивать строку, где есть максимальный элемент, и затем вычеркивать столбцы, где есть элементы, отмеченные в вычеркнутой строке, и т.д. Вычеркнутые строки и столбцы являются выделенными.

Продолжим решение. Как следует из анализа матрицы ⁽¹⁾, решение x⁽¹⁾ не является оптимальным. Следующее решение получаем с помощью цикла, построенного на клетке (2,4), имеющей максимальную оценку. Перемещая по циклу , получаем

В новом плане перевозок транспортные затраты равны

Используя полученный план, преобразуем матрицы ⁽¹⁾ в матрицу оценок ⁽¹¹⁾. Результат представлен ниже.

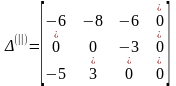
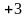
Из анализа этой матрицы следует, что план X⁽¹¹⁾ не является оптимальным. Находим в матрице ⁽¹¹⁾ максимальный элемент, и на соответствующей этому элементу клетки в X⁽¹¹⁾ строим цикл пересчета.

Вычисляем по нечетным клеткам цикла 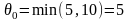и, перемещая полученное значение по циклу пересчета, приходим к следующему плану перевозок

.

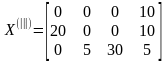По этому плану значение критерия 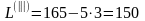. Для выяснения статуса нового плана находим соответствующую ему матрицу оценок путем преобразования матрицы ⁽¹¹⁾, в результате имеем

.

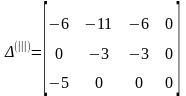Матрица ^(III) не содержит положительных оценок, следовательно, план 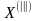является оптимальным. Согласно этому плану от 1-го поставщика надо поставить 10 ед. продукции 4-му потребителю, от 2-го поставщика 20 ед. направить 1-му и 10 ед. 4-му потребителям, от 3-го поставщика 5, 30 и 5 ед. – соответственно 2, 3 и 4 потребителям.

Контрольные вопросы к первому заданию

1. Что такое базисное решение задачи ЛП?

2. Сколько оптимальных решений имеет задача?

3. Чему равна размерность базиса в транспортной задаче?

4. Как несбалансированную задачу привести к сбалансированной?

5. Как строится цикл пересчета?

6. К чему приведет перемещение по циклу, построенному на клетке с отрицательной оценкой?

7. В чем состоит признак оптимальности транспортной задачи?

8. Как интерпретировать результаты решения в случае несбалансированной задачи?

ЗАДАНИЕ ВТОРОЕ

Решить задачу целочисленного программирования методом ветвей и границ. Корневую задачу решить симплекс-методом, остальные графически. Построить дерево решений.

Для выполнения этого задания следует проработать материал гл.7 в [3], особенно разд. 7.1 и 7.3. Там же приведены примеры решения.

Обратите внимание, что каждая задача из дерева решений решается как непрерывная, то есть без требования целочисленности. При поиске оптимального решения графическим методом надо выделить допустимую область решаемой задачи и на ней с помощью линии уровня критерия определить оптимальную вершину. По уравнениям границ, пересечение которых образует найденную вершину, находятся координаты вершины, то есть значения переменных, а по ним – значение критерия (оценки).

Варианты задания

№1	L=7x1 + 4x2  max 4x1 + x2  14 3x1 + 2x2  12 xj  0, цел.	№2	L= 2x1 + 3x2  min 7x1 + 20x2  140 2x1 + x2  18 xj  0, цел.
№3	L=6x1 + 4x2  min 4x1 + 2x2  7 x1 – x2  1 xj  0, цел.	№4	L= 6x1 + 9x2  max 5x1 + 7x2  35 4x1 + 9x2  36 xj  0, цел.
№5	L=4x1 + 4x2  max 3x1 + 2x2  10 x1 + 2x2  9 xj  0, цел.	№6	L= 2x1 + 7x2  max 4x1 + 5x2  20 – x1 + 2x2  1 xj  0, цел.
№7	L=6x1 + 9x2  max 8x1 + 18x2  72 5x1 + 7x2  35 xj  0, цел.	№8	L= –2x1 – 3x2  min 5x1 + 7x2  35 4x1 + 9x2  36 xj  0, цел.
№9	L=9x1 + 12x2  max 14x1 + 9x2  51 – 6x1 + 3x2  1 xj  0, цел.	№10	L= x1 + x2  min 2x1 + 4x2  7 10x1 + 3x2  15 xj  0, цел.
№11	L=6x1 + 8x2  max – 12x1 + 6x2  1 14x1 + 9x2  51 xj  0, цел.	№12	L= 9x1 + 12x2  max –12x1 + 6x2  2 14x1 + 9x2  51 xj  0, цел.
№13	L= 14x1 + 8x2  max 6x1 + 4x2  24 4x1 + x2  14 xj  0, цел.	№14	L= 2x1 + 6x2  max 10x1 + 11x2  110 – x1 + 2x2  7 xj  0, цел.
№15	L= 4x1 + 6x2  max 10x1 + 14x2  70 4x1 + 9x2  36 xj  0, цел.	№16	L= 6x1 + 8x2  max 6x1 –3x2  – 1 14x1 + 9x2  51 xj  0, цел.
№17	L=x1 + x2  max 2x1 + 5x2  16 6x1 + 5x2  27 xj  0, цел.	№18	L= 2x1 + 7x2  max – 2x1 + 4x2  2 4x1 + 5x2  20 xj  0, цел.
№19	L=x1 + x2  max 4x1 + 5x2  18 – x1 + 2x2  1 xj  0, цел.	№20	L= 4x1 + 14x2  max 8x1 + 10x2  40 – 2x1 + 4x2  2 xj  0, цел.
№21	L=3x1 + 3x2  min 4x1 + 8x2  14 10x1 + 3x2  15 xj  0, цел.	№22	L= x1 + x2  max 2x1 + 11x2  38 4x1 –5x2  5 xj  0, цел.
№23	L=7x1 + 2x2  max 4x1 + x2  14 6x1 + 4x2  24 xj  0, цел.	№24	L=x1 + x2  max 4x1 + 5x2  18 –x1 + 2x2  1 xj  0, цел.
№25	L=8x1 + 5x2  max x1 + x2  6 9x1 + 5x2  45 xj  0, цел.	№26	L=5x1 + 9x2  max –6x1 + 3x2  1 2x1 + 5x2  28 xj  0, цел.
№27	L= x1 –x2  min 2x1 + x2  6 – 5x1 + 2x2  0 xj  0, цел.	№28	L= 4x1 + 3x2  max 6x1 – 12x2  1 9x1 + 14x2  51 xj  0, цел.
№29	L=3x1 + 2x2  min 20x1 + 7x2  140 x1 + 2x2  18 xj  0, цел.	№30	L=x1 + x2  max 5x1 + 4x2  18 2x1 – x2  1 xj  0, цел.
№31	L= 2x1 + 3x2  max 5x1 + 7x2  70 4x1 + 9x2  72 xj  0, цел.	№32	L=13x1 – 6x2  max 12x1 + 11x2 132 4x1 – 5x2  20 xj  0, цел.
№33	L=–11x1 + 6x2  min 12x1 + 11x2 132 –x1 + 2x2 2,2 xj  0, цел.	№34	L=11x1 – 6x2  max 8x1 + 13x2 104 –x1 + 2x2 2,2 xj  0, цел.
№35	L= 7x1 + 3x2  max 5x1 + 2x2  20 4x1 + 2x2  19 xj  0, цел.	№36	L=4x1 + 7x2  max x1 + 4x2  14 2x1 + 3x2  12 xj  0, цел.
№37	L=x1 + x2  max 11x1 + 2 x2  38 –5x1 + 4x2  5 xj  0, цел.	№38	L=5x1 + 1,6x2  max –0,6x1 + x2  2,5 5x1 + 1,5x2  22,5 xj  0, цел.
№39	L=25x1 + 8x2  max x1 + 0,3x2  4,5 –1,2x1 + x2  5 xj  0, цел.	№40	L=5x1 + 2x2  max 12x1 + 11x2 132 –x1 + 2x2 2,2 xj  0, цел.
№41	L=–11x1 + 6x2  min 12x1 + 11x2 130 –x1 + 2x2 2,2 xj  0, цел	№42	L=19x1 + 6x2  max 10x1 + 3x2  45 –6x1 + 5x2  25 xj  0, цел.
№43	L=x1 + 2x2  min 5x1 + 7x2 17,5 2x1 + 5,5x2 11 xj  0, цел	№44	L=–x1 + 3x2  max 23x1 + 40x2  184 –11x1 + 10x2  22 xj  0, цел.

Контрольные вопросы ко второму заданию

1. Как изменяется допустимое множество задачи ЛП при добавлении требования целочисленности переменных?

2. В каких случаях обрывается ветвь дерева решений?

3. При выполнении каких условий порождаются две новые задачи? В каком порядке эти условия проверяются?

4. Условие завершения работы алгоритма?

5. Что такое рекорд?

6. Что такое верхняя граница в задаче на максимум?

7. Как соотносятся допустимые множества задач, лежащих в разных ветвях?

8. При каких исходных параметрах алгоритма не найдется решение разрешимой задачи?

9. От чего зависит число непрерывных задач, решаемых в методе ветвей и границ?

10. Как изменяется значение критерия задач и почему при движении вниз по ветви?

11. Алгоритм дает точное или приближенное решение целочисленной задачи?

12. Метод применяется для полностью целочисленных задач или для смешанных, или для тех и других?

13. После завершения алгоритма, по какому признаку можно быстро определить – задача имеет решение или нет?

14. Какое решение находит алгоритм: локальное или глобальное? Обоснуйте ответ.

15. Метод ветвей и границ содержит или нет признак оптимальности?