
- •Методические указания
- •И задания по дисциплинам
- •Системный анализ и исследование операций
- •Теория принятия решений
- •Краткие методические указания по самостоятельному изучению курса
- •Задания на контрольные работы и указания к их выполнению
- •Контрольная работа №1
- •Варианты заданий
- •Контрольная работа №2
- •Краткая теория и пояснения к решению
- •Метод потенциалов.
- •Дополнительный материал к решению корневой задачи
- •Вопросы к экзамену по са и ио
- •Указания к дисциплине «Теория принятия решений»
- •Литература к реферату по тпр
- •Примерные темы рефератов
Краткая теория и пояснения к решению
Модель сбалансированной Т-задачи.
Критерий:
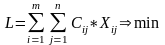 (1)
(1)
 (2)
(2)
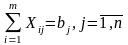 (3)
(3)
 ,
(4)
,
(4)
где
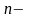 число
пунктов отправления (ПО),
число
пунктов отправления (ПО),
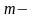 чисто
пунктов назначения (ПН),
чисто
пунктов назначения (ПН),
 затраты на перевозку единицы груза,
затраты на перевозку единицы груза,
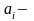 количество
груза в пункте отправления (производственная
мощность),
количество
груза в пункте отправления (производственная
мощность),
 потребность
в грузе в пункте назначения,
потребность
в грузе в пункте назначения,
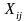 -количество
груза, перевозимого из i-го
пункта отправления в j-й
пункт назначения.
-количество
груза, перевозимого из i-го
пункта отправления в j-й
пункт назначения.
Задача сбалансирована, если суммарные потребности равны суммарным возможностям:
 (5)
(5)
Особенности модели:
Переменные в условиях задачи входят только с коэффициентом единица.
В условиях мы имеем 2 системы ограничений: (2) и (3).
Каждая переменная входит в первую группу условий один и только один раз и во 2-ую группу условий один и только один раз.
Число переменных равно m
 n.
n.Для разрешимости Т-задачи необходимо и достаточно чтобы она была сбалансированной. Если условие (5) выполняется, то в задаче заведомо имеется хотя бы одно оптимальное решение.
Решение Т-задачи методом потенциалов
Т-задача должна быть сбалансирована. Если она не сбалансирована, то добавляется фиктивный поставщик (строка) или фиктивный потребитель (столбец) с нулевыми затратами и количеством груза, равным дебалансу.
Сначала строится начальное базисное решение. Базисные решения называют также планами перевозок. Размерность базисного решения равна m+n-1.
Способы построения начального плана:
правило северо-западного угла;
правило минимального элемента;
метод Фогеля;
Общий принцип определения значений базисных переменных в начальном плане: на каждом шаге необходимо очередной базисной переменной присваивать максимально-допустимое значение, а оно определяется как минимум из того. что не довезли в ПН, и того, что не вывезли из ПО..
Правило северо-западного угла
Заполняем таблицу начиная с левого верхнего (северо-западного) угла, двигаясь далее по строке вправо, если полностью удовлетворили потребность ПН, или по столбцу вниз, если все забрали из ПО.
Занесем в клетку (1,1) меньшее значение из a1 и b1 , т.е.
 .
.
Если a1>b1
, то
 и первый столбец «закрыт» для заполнения
остальных его клеток, т.е.
и первый столбец «закрыт» для заполнения
остальных его клеток, т.е.
 для
для
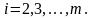 (потребности
первого потребителя удовлетворены
полностью).
(потребности
первого потребителя удовлетворены
полностью).
Двигаясь далее по первой строке, записываем в соседнюю клетку (1,2) меньшее из чисел a1-b1 и b2 т.е.

Если же b1>a1,
то аналогично «закрывается» первая
строка, т.е.
 для
для
 Переходим к заполнению соседней клетки
(2,1), куда заносим
Переходим к заполнению соседней клетки
(2,1), куда заносим
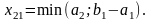
Заполнив вторую клетку (1,2) или (2,1), переходим к заполнению следующей клетки либо по второй строке, либо во втором столбце. Этот процесс продолжается до полного исчерпания груза у поставщиков или полного удовлетворения потребностей. Заполнение последней клетки (m,n) одновременно «закроет» столбец n и строку m.
План, полученный по правилу северо-западного угла, будет опорным планом системы ограничений задачи.
Пример:
Найти опорный план транспортной задачи по правилу северо-западного угла.
Поставщик (ПО) |
Потребитель (ПН) |
Запасы груза |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
6 |
7 |
3 |
5 |
100 |
A2 |
1 |
2 |
5 |
6 |
150 |
A3 |
3 |
10 |
20 |
1 |
50 |
Потребность в грузе |
75 |
80 |
60 |
85 |
300\300 |
Как видно из правой нижней клетки, потребности равны возможностям (300), т.е. задача сбалансированная. Ход построения начального плана показан стрелками.
Поставщик |
Потребитель |
Запасы груза |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
6 75
|
7 25
|
3 |
5 |
100 |
A2 |
1 |
2 55 |
5 60 |
6 35 |
150 |
A3 |
3 |
10 |
20 |
1 50 |
50 |
Потребность в грузе |
75 |
80 |
60 |
85 |
300 |
Тарифы (удельные затраты) перевозок размещены в правом верхнем углу каждой клетки таблицы, а значения перевозимого по плану груза показаны серым цветом. Как видно, получено 6 положительных переменных, т.е. их число равно m +n-1=3+4-1=6. Суммарные затраты по этому плану равны 6*75+7*25+2*55+5*60+6*35+1*50=1295.
Правило минимального элемента
Сущность его состоит в том, что на каждом шаге осуществляется максимально возможная поставка в клетку с минимальным тарифом Сik. Заполнение таблицы начинаем с клетки, которой соответствует наименьший элемент Сik из всей матрицы тарифов. Затем остаток по столбцу или строке помещаем в клетку того же столбца или строки, которой соответствует следующее по величине значение Сik, в столбце или строке и т.д. Иными словами, последовательность заполняемых клеток определяется по величине Сik, а помещаемые в этих клетках значения Xik – как в правиле «северо-западного угла».
Пример:
Найти опорный план по правилу «минимального элемента» для задачи, представленной в следующей таблице:
Поставщик |
Потребитель |
Запасы груза |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
6 |
7 |
3 |
5 |
100 |
A2 |
1 |
2 |
5 |
6 |
150 |
A3 |
3 |
10 |
20 |
1 |
50 |
Потребность |
75 |
80 |
60 |
85 |
300\300 |
Решение:
Наименьшие тарифы соответствуют клеткам (2,1), (3,4):
С21=С34=1.
Поместим максимально возможное
количество груза, например, в клетку
(2,1) - x21=75,
остаток груза помещаем в клетку (2,2), в
которой тариф С22=2 наименьший
из всех в этой строке, т.е.
 Второму потребителю еще необходимо 5
единиц груза (80-75). В клетку (1,2) от
поставщика А1 помещаем
Второму потребителю еще необходимо 5
единиц груза (80-75). В клетку (1,2) от
поставщика А1 помещаем
 единиц груза.
единиц груза.
Далее по первой строке в клетку (1,3) , имеющей наименьший тариф, заносим необходимое количество груза
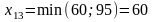 единиц груза.
единиц груза.
Остаток груза от поставщика А1 заносим в клетку (1,4), т.е.
 единиц груза.
единиц груза.
Спрос четвертого потребителя удовлетворен не полностью, поэтому находим в этом столбце клетку (3,4) с наименьшим тарифом и помещаем в нее количество груза x34=50 единиц.
В результате проведенных назначений получаем опорный план:
Поставщик |
Потребитель |
Запасы груза |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
6
|
7 5 |
3 60 |
5 35 |
100 |
A2 |
1
|
2 75
|
5
|
6
|
150 |
A3 |
3 |
10 |
20 |
1 50 |
50 |
Потребность в грузе |
75 |
80 |
60 |
85 |
300 |
или в матричном виде
 .
.
Этому плану соответствуют суммарные затраты 7*5+3*60+5*35+1*75+2*75+50*1=665, что существенно меньше, чем в предыдущем плане.
Замечание: Может оказаться, что при построении плана перевозок занятых клеток (xij>0) будет меньше, чем m +n-1. В этом случае задача называется вырожденной (есть нулевые базисные переменные). Вырожденность может иметь место как в начальном плане, так и в последующих. Если столкнетесь с таким планом, имейте в виду, что клетка с базисным нулем «обладает» всеми «правами» базисной клетки.



 75
75
