2.3. Пример расчета
Для бетонной колонны, сжатой силой Р, приложенной в точке 4 верхнего сечения колонны (рис. 2.7), требуется:
Рис. 2.7. Поперечное сечение колонны
выбрать исходные оси и определить моменты инерции сечения относительно этих осей;
определить положение центра тяжести и провести главные центральные оси;
вычислить главные центральные моменты инерции и радиусы инерции поперечного сечения;
построить ядро сечения;
построить нейтральную ось и определить координаты опасных точек сечения;
определить нормальные напряжения в характерных точках верхнего сечения колонны в долях силы Р;
построить в аксонометрии эпюру нормальных напряжений для верхнего сечения колонны;
подобрать допускаемую величину силы Р с учетом собственного веса колонны.
Числовые данные: a = 2 м; h = 9 м; = 5 МПа; = 0,6 МПа;
= 17 .
Изобразим сечение в масштабе (рис. 2.8).
Рис. 2.8. Простейшие элементы сечения
Выберем исходные оси , . Ось проходит через нижние точки сечения, ось совпадает с осью симметрии сечения.
Разбиваем сечение на простейшие части, геометрические характеристики которых определяем по готовым формулам, приведенным в таблице приложения 1:
половина круга
.
;
;
.
прямоугольник
,
.
;
.
прямоугольник
,
.
;
.
Определяем моменты инерции сечения
относительно исходных осей
,
:
Здесь
.
Главная центральная ось y
совпадает с осью симметрии
и поэтому главный центральный момент
Положение главной центральной оси х определяется по формуле:
,
где
;
.
Учитывая числовые значения
и F, получим
=
=1,57м.
Отложив
от оси
,
проводим главную центральную ось
параллельно исходной оси
.
Вычисляем момент инерции относительно
этой оси
.
Вычисляем радиусы инерции:
;
;
;
.
Для построения ядра сечения достаточно провести восемь касательных нулевых линий (рис. 2.9).
Рис. 2.9. Ядро сечения и эпюра нормальных напряжений
Отрезки, отсекаемые линиями на осях х и у измеряем на рисунке:
-
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
Вычисляем координаты полюсов, соответствующих нулевым линиям по формулам (2.6):
-
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
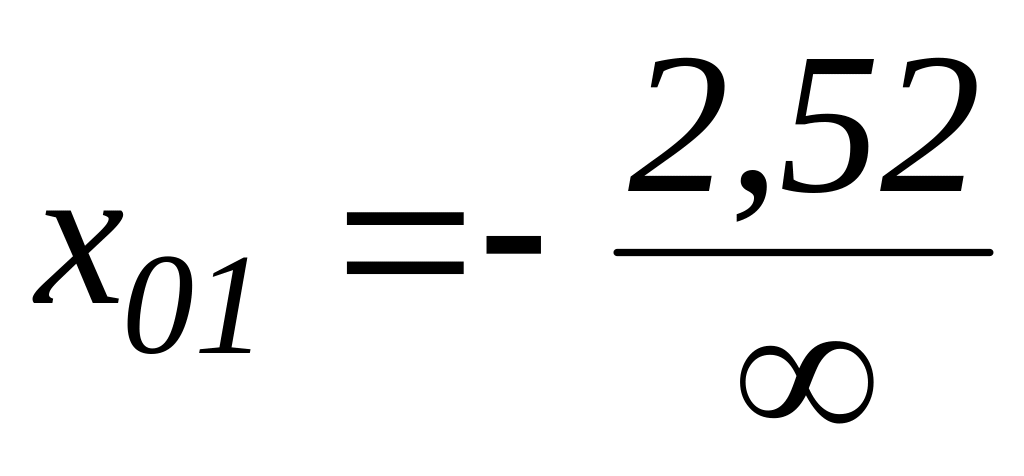По координатам стоим полюсы 1, 2, 3, 4, 5, 6, 7, 8 (рис. 2.9). На участке 2, 3,…, 8 каждая следующая нулевая линия может быть получена в результате вращения предыдущей нулевой линии около фиксированной угловой точки. При этом полюс перемещается по прямой. Поэтому соединим полюсы последовательно прямыми линиями. На участке 8, 1, 2 соединим полюсы плавной кривой. Таким образом ограничиваются контуры ядра сечения.
Сжимающая сила приложена в точке 4. Обозначим ее цифрой 0.
Координаты этой точки:
;
.
Отрезки, отсекаемые нулевой линией на осях х и у соответственно равны
;
.
Отложим отрезок а на оси х, отрезок b на оси у и проведем нулевую линию n-n (рис. 2.9). Нулевая линия делит сечение на растянутую и сжатую зоны.
Опасными точками сечения являются точки 1 и 0, максимально удаленные от нулевой линии. Напряжения в этих точках найдем по формуле (2.3)
.
В точке 1 с координатами
=3м;
=
-1,07м действует наибольшее
растягивающее напряжение
.
В точке 0 с координатами
=
-3м;
=0,93м
действует наибольшее сжимающее напряжение
.
Эпюра нормальных напряжений, значения которых отложены от линии, перпендикулярной к нейтральной оси, показана на рис. 2.9. Каждая ордината этой эпюры определяет величину нормальных напряжений, возникающих в точках поперечного сечения, расположенных на прямой, проходящей через эту ординату параллельно нейтральной оси.
С помощью этой эпюры были найдены напряжения во всех характерных точках сечения (рис. 2.9) и построена в изометрии эпюра нормальных напряжений для верхнего сечения колонны (рис. 2.10).
Подбираем величину нагрузки Р с учетом собственного веса колонны.
Условие прочности по растягивающим напряжениям имеет вид:
,
где
.
Таким образом
;
откуда Р=2069 кН.
Условие прочности по сжимающим напряжениям имеет вид:
,
где
.
Таким образом
;
откуда Р=11822 кН.
Из двух значений Р за допускаемое принимаем меньшее:
Р=2069 кН.
Рис. 2.10. Пространственная эпюра нормальных напряжений