Механика

РАБОТА № 1

Изучение явления удара шаров

Цель работы: Экспериментально доказать выполнение закона сохранения импульса при ударе шаров, определить коэффициент восстановления энергии при упругом и неупругом ударах.

Оборудование: баллистический маятник, весы.

Описание метода

Удар – это процесс кратковременного взаимодействия тел, при котором происходит значительное изменение скоростей тел, сравнимое с их скоростями до удара. Согласно второму закону Ньютона вследствие кратковременности удара силы взаимодействия могут быть очень велики. Поэтому на время удара можно пренебречь внешними силами, например, силой трения шаров о воздух, по сравнению с внутренними силами и считать систему соударяющихся тел замкнутой. В замкнутой системе тел выполняется закон сохранения импульса: импульс системы тел не изменяется:

, (1)

где и – скорости тел до и после взаимодействия.

Различают два предельных вида, две идеализации реального удара: абсолютно упругий и абсолютно неупругий удары.

При абсолютно упругом ударе тела в первой фазе удара упруго деформируются. При этом часть кинетической энергии превращается в потенциальную энергию упругой деформации. Затем во второй фазе тела под действием упругих сил расходятся, форма тел восстанавливается, и потенциальная энергия деформации тел полностью превращается обратно в кинетическую. В результате кинетическая энергия тел до и после удара одинакова. Таким образом, суммарная механическая энергия в процессе абсолютно упругого удара сохраняется.

При абсолютно неупругом ударе тела деформируются неупруго, пластически. Тела после удара движутся совместно, их скорости одинаковы и это является признаком абсолютно неупругого удара. Часть кинетической энергии превращается в работу неупругого пластического деформирования тел, во внутреннюю энергию. Поэтому механическая энергия при неупругом ударе не сохраняется, происходит ее диссипация (рассеяние).

Диссипацию механической энергии при реальном ударе характеризуют коэффициентом восстановления энергии , который определяется как отношение суммарной кинетической энергии тел после удара к их энергии до удара:

.

Величина коэффициента восстановления энергии зависит от упругих свойств соударяющихся тел, их скоростей и масс. Для абсолютно упругого удара, при котором механическая энергия сохраняется, = 1. В других реальных случаях .

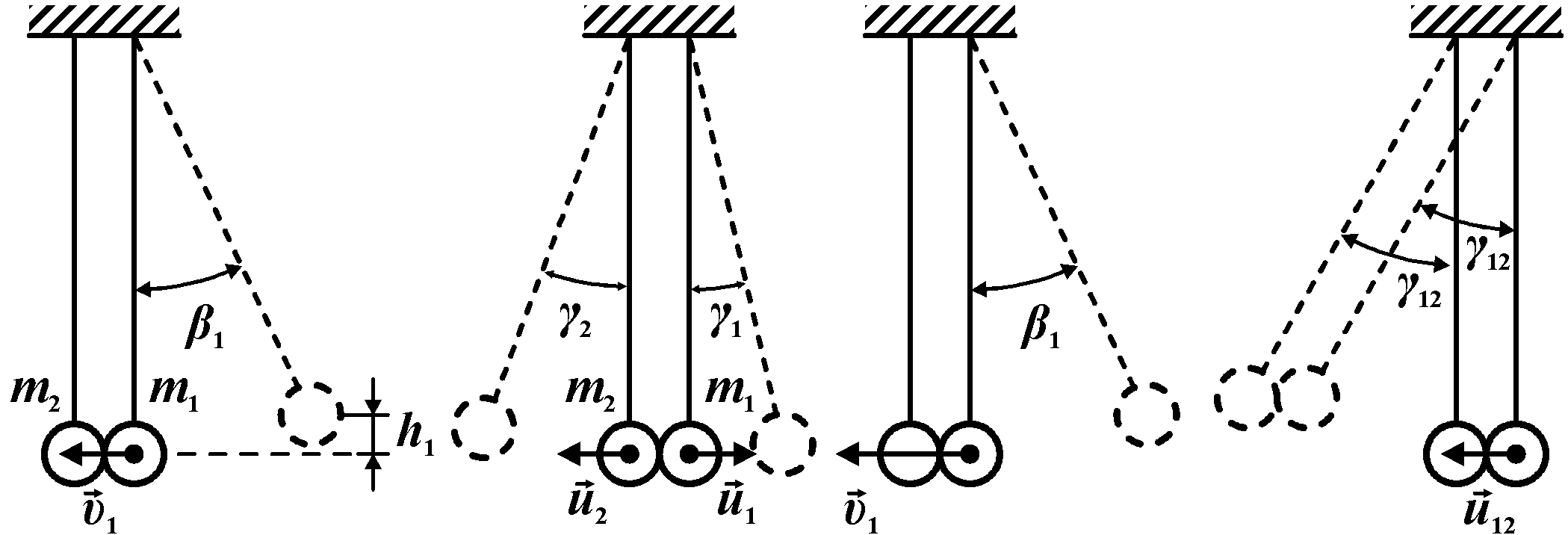
Рассмотрим прямой, центральный удар двух шаров, при котором скорости шаров перед ударом направлены вдоль прямой, проходящей через их центры масс. Центры масс лежат на линии удара, т.е. на нормали к поверхности шаров в точке соприкосновения.

Упругий удар Неупругий удар

До удара После удара До удара После удара

Схема соударения шаров

Пусть правый шар массой со скоростью налетает на покоящийся левый шар массой , = 0. Запишем закон сохранения импульса для упругого и неупругого ударов в проекции на ось, направленную по скорости :

, (2)

. (3)

Здесь и – скорости правого и левого шаров после упругого удара, – скорость шаров, движущихся совместно после неупругого удара.

Для проверки выполнения закона сохранения импульса по уравнениям (2) и (3) определим скорости шаров через легко измеряемые углы отклонения нитей от положения равновесия. Если пренебречь сопротивлением воздуха и учесть, что в данном случае в системе действуют только консервативные силы, то при движении, например, правого шара, висящего на нити длиной , по закону сохранения механической энергии

. (4)

Высота падения шара . Для малых углов отклонения , выраженных в радианах, справедливо приближенное равенство и . Следовательно, скорость шара в момент перед ударом пропорциональна углу отклонения его от положения равновесия, выраженному в радианах. Аналогично можно определить , , . Здесь углы должны быть выражены в радианах.

Подставив формулы для скоростей в уравнение закона сохранения импульса (2) и (3), получим уравнения, которые можно проверить на опыте и сделать выводы о сохранении импульса при упругом и неупругом ударах для баллистического маятника:

, (5)*

. (6)*

Введем обозначения величин, пропорциональных значениям импульсов шаров при упругом и неупругом соударениях:

; ; .

Для получения формулы коэффициента восстановления энергии при ударе подставим сначала формулы для скоростей в выражения кинетической энергии. Например,

,

а затем выражения для кинетической энергии в формулы коэффициентов восстановления энергии для упругого и неупругого ударов:

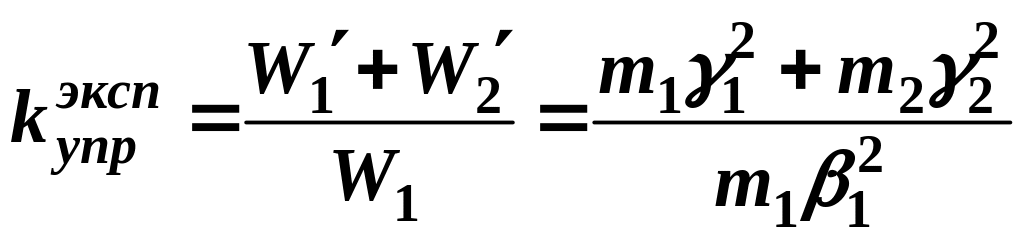, (7)*

. (8)*

В уравнениях (5) – (8) – угол отклонения правого шара перед ударом, и – углы отклонения правого и левого шаров после упругого удара, – угол отклонения обоих шаров после неупругого удара (см. рисунок).

Теоретическое значение коэффициентов восстановления энергии для упругого удара = 1, а для неупругого при вычисляется по формуле:

. (9)*

Получим формулы для оценки погрешностей измеряемых величин при одном из ударов, например, неупругом Условно примем, что измерения равноточные и погрешности измеряемых величин при упругом ударе можно оценивать по этим же формулам Погрешность величины при многократных косвенных измерениях складывается из систематической и случайной погрешностей.

Для получения формулы систематической относительной погрешности вначале уравнение (6) прологарифмируем, а затем продифференцируем и заменим знак дифференциала на знак систематической погрешности (см. раздел «Методы обработки результатов измерений»), получим:

= = _, (10)

где = , (в радианах), – систематические абсолютные погрешности при прямых измерениях массы и угла отклонения шаров (численные значения этих величин приведены в табл. 1). Расчеты показывают, что относительные систематические погрешности измерения масс в несколько раз меньше относительных систематических погрешностей измерения углов отклонения и ими можно пренебречь.

Систематическая абсолютная погрешность:

(11)

Случайные абсолютные погрешности измерения углов и величины связаны соотношением: = . Остальные величины в исходной формуле (6) измерялись один раз, поэтому их случайные погрешности равны нулю.

Случайная абсолютная погрешность прямых измерений углов отклонения рассчитывается по формуле (2) (см. раздел «Методы обработки результатов измерений»):

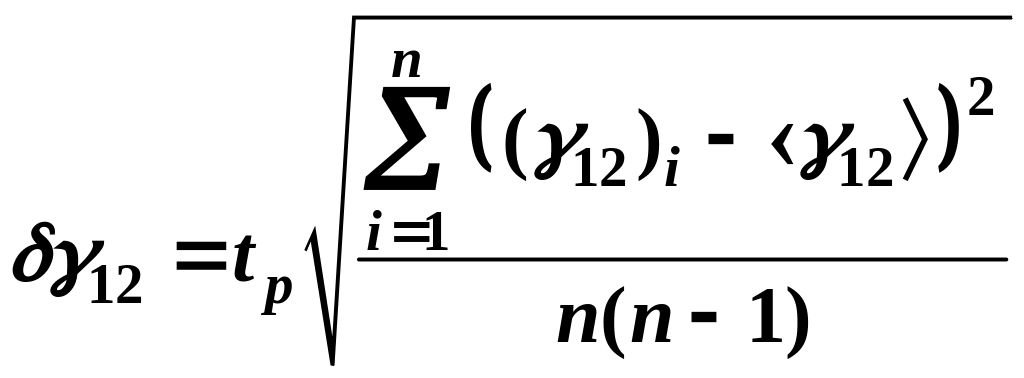. (12)

Доверительная граница суммарной абсолютной погрешности величины :

= = . (13)

Расчеты показывают, что систематическая погрешность в несколько раз меньше случайной погрешности и ей можно пренебречь, что и учтено в формуле (13).

Найдем формулу для оценки абсолютной и случайной погрешностей среднего значения коэффициента восстановления энергии для неупругого удара. По аналогии с формулами (10), (11), (13), пренебрегая систематическими погрешностями, получим:

= . (14)*