6. Изучение явления дифракции плоских световых волн на одной и двух щелях при помощи лазера

ЦЕЛЬ РАБОТЫ

Цель работы заключается в изучении дифракции Фраунгофера от одной и двух щелей с использованием лазерного источника света. Содержание лабораторной работы состоит в определении положений максимумов или минимумов и проверке распределения интенсивности в картине дифракции от одной и двух щелей при наблюдении в свете лазера.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями (например, вблизи границ непрозрачных или прозрачных тел, сквозь малые отверстия и т.п.) и связанных (явлений) с отклонениями от законов геометрической оптики. При дифракции, как и при интерференции, происходит перераспределение интенсивности колебаний в пространстве в результате суперпозиции когерентных волн.

Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов. При этом разность фаз δ колебаний, возбуждаемых (в точке наблюдения) (любыми) двумя различными волнами, остается постоянной во времени.

Дифракция света на одной щели.

В случае дифракции света на узкой щели, ширина которой одного порядка с длиной волны падающего излучения, волновой фронт в плоскости щели можно считать плоским, причем, согласно принципу Гюйгенса, каждую точку этого плоского фронта волны можно рассматривать как источник вторичных волн. Дальнейшее взаимодействие этих волн между собой можно объяснить как суперпозицию (наложение) волновых компонент (по Френелю) с разными фазами, обусловленными различными длинами пути от точек щели (источников вторичных волн) до точки наблюдения Р на экране.

Пусть на узкую щель шириной "b" нормально к ее плоскости падает монохроматическая плоская волна. Проведем ось координат ОХ поперек щели в ее плоскости, выбирая за начало отсчета точку О на краю щели (см.рис. 1).

Р азобьем поверхность щели (фронта волны) на узкие полоски шириной dx, параллельные длинным краям щели. Согласно принципу Гюйгенса-Френеля каждая полоска (каждый элемент фронта волны или волновой поверхности) является источником вторичной сферической волны, которая вызывает колебания с амплитудой прямо пропорциональной площади полоски, т.е. ширине полоски dx. Собирающая линза, поставленная за щелью, собирает вторичные параллельные лучи в точке Р своей фокальной плоскости (рис.1). Если направление вторичных лучей совпадает с направлением лучей, падающих на щель, т.е.  = 0, то колебания в точке Р, вызванные разными вторичными лучами, имеют одинаковые фазы

,

где С  некоторая постоянная. Интегрируя это равенство по всей поверхности щели и обозначая амплитуду колебаний в фокальной плоскости линзы при  = 0 буквой А₀, получим

.

Отсюда .

Рассмотрим вторичные лучи, отклонившиеся при дифракции от направления падающих лучей на угол   0. Так как фронт волны (волновая поверхность) параллельных лучей перпендикулярен лучам, то фронт волны лучей, отклонившихся на угол  пересекает плоскость чертежа по линии ONBN, а фронт волны падающих лучей - по линии ОВ. До ОВ и после ON до точки Р оптическая длина хода лучей, проходящих через разные точки щели, одинакова, а между ОВ и ON - разная. В частности, длина хода вторичного луча, испускаемого точкой К с координатой х, больше длины хода луча, испускаемого точкой О на величину . Это вызывает запаздывание фазы колебаний на величину . Поэтому в точке Р фокальной плоскости линзы складываются колебания , вызванные вторичными лучами от всех точек щели, т.е. при изменении х от О до "b":

. (1)

Из формулы (1) видно, что Е_ зависит от времени t по гармоническому закону, причем амплитуда колебаний А_ для лучей, отклонившихся при дифракции на угол , в точке Р фокальной плоскости линзы равна

.

Так как интенсивность света I прямо пропорциональна квадрату амплитуды А², то в фокальной плоскости линзы интенсивность света I_ равна

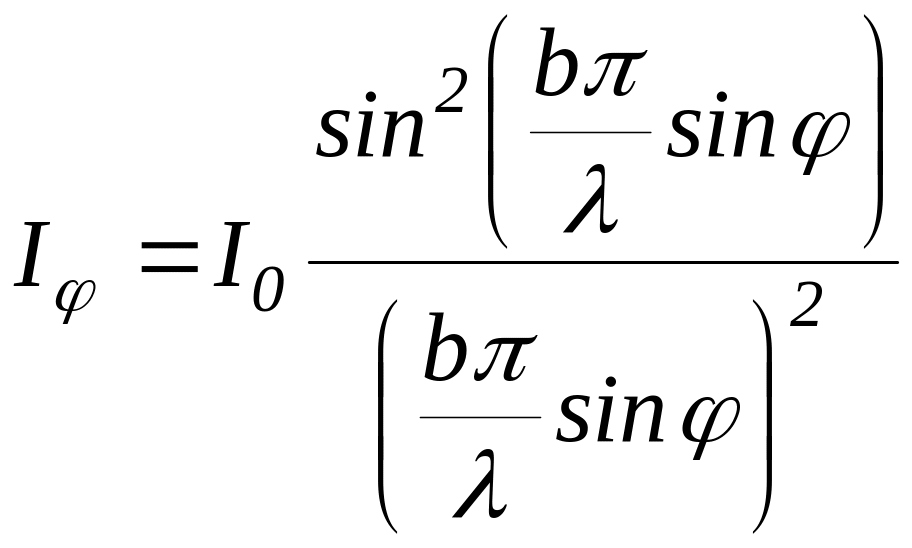. (2)

На рис.2 представлено распределение интенсивности света , дифрагированного на одиночной щели шириной "b". По оси абсцисс отложены значения .

Из (2) следует, что при углах

(3)

т.е в случае, если

, (к = 1,2,3...), (4)

интенсивность обращается в нуль.

Итак, условие (4) определяет положение минимумов интенсивности при дифракции Фраунгофера на одной щели.

Между минимумами интенсивности расположены максимумы, положение которых может быть определено уравнением , имеющим корни ; ; и т.д. Значения интенсивности в максимумах быстро убывает с увеличением порядка максимумов.

Численные значения интенсивностей главного и следующих максимумов относятся как

(5)

Из (5) видно, что основная часть светового потока сосредоточена в центральной дифракционной полосе, расположенной между минимумами первого порядка.

Из (4) следует, что угловая ширина главного максимума при условиях к = 1 и равна

. (6)

При увеличении ширины щели (b) угловая ширина максимумов уменьшается, при этом главный (или центральный) максимум становится резче и первые минимумы приближаются к центру дифракционной картины (На рис. 3 b₂ > b₁).