Логические операции над высказываниями

В дальнейшем будем обозначать:

• элементарные высказывания строчными буквами латинского алфавита: a, b, …, z;

• истинное значение высказывания «И» или «1»;

• ложное значение высказывания «Л» или «0»;

Если высказывание х истинно, то будем писать х=1;

Если высказывание х ложно, то будем писать х=0;

Употребляемые в обычной речи связки «и», «или», «не», «если …, то …», «тогда и только тогда, когда …» и т.п. позволяет из уже заданных высказываний строить новые сложные высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности или ложности исходных высказываний и соответствующей трактовки связок как логических операций над высказываниями.

Логическая операция может быть полностью описана таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний.

В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:

Логическая связка	Названия логической операции	Обозначения
не	Отрицание, инверсия	,ֿ⌐
и, а, но, хотя	Конъюнкция, логическое умножение	&, ∙,
или	Дизъюнкция, логическое сложение, нестрогая дизъюнкция	, +
либо	Строгая дизъюнкция, исключающее «ИЛИ», сложение по модулю 2	, ∆
если …, то	Импликация, следование	 , →
тогда и только тогда, когда	Эквивалентность, эквиваленция, равнозначность	 , ~ , ≡, ↔

Введем перечисленные логические операции формальным образом.

1. Отрицание

Отрицанием высказывания х называется новое высказывание, которое является:

истинным – если высказывание х ложно,

ложным – если высказывание х истинно.

Другими словами, отрицание – это логическая операция, которая каждому элементарному высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

Отрицание высказывания х обозначается 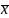или ¬х

Читается «не х» или «неверно, что х».

Таблица истинности для :

х
0	1
1	0

Примеры:

1. Отрицанием высказывания {У меня дома есть компьютер} будет высказывание {Неверно, что у меня дома есть компьютер} или { У меня дома нет компьютера}

2. Отрицанием высказывания {Я не знаю корейского языка} будет высказывание { Неверно, что я не знаю корейского языка } или { Я знаю корейский язык}

3. Отрицанием высказывания {Все юноши 11-х классов – отличники} будет высказывание {Не все юноши 11-х классов – отличники} или {Некоторые юноши 11-х классов – не отличники}

4. Высказывание {Все юноши 11-х классов – не отличники } не является отрицанием высказывания {Все юноши 11-х классов –отличники }. Объясняется это следующим образом: среди 11-классников есть как отличники, так и не отличники.

5. Для высказывания {На стоянке стоят красные «Жигули»} следующие предложения высказываниями являться не будут:

   1. {На стоянке стоят не красные «Жигули»}

   2. {На стоянке стоит белый «Мерседес»}

   3. {Красные «Жигули» стоят не на стоянке}

Пусть х – высказывание. Так как также является высказыванием, то можно образовать отрицание высказывания , то есть высказывание , которое называется двойным отрицанием высказывания х. Ясно, что логические значения х и совпадают.