V. Решить лнду двумя способами:

а) методом неопределенных коэффициентов;

б) методом вариации произвольных постоянных.

у″-7у′+6у=х², у(0)=2, у′(0)=-7.

Типовой расчет по теме «Дифференциальные уравнения второго порядка»

Вариант 7

І. Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами.

1) у″-2ау′+ а²у=0; 3) у″+4у=0;

2) у″-7у′=0; 4) у^v -у'''=0.

ІІ. Применяя метод вариации произвольных постоянных, решить ЛНДУ:

1) у″+у=1/sinx; 2) у″+у=2сtgх.

ІІІ. Указать вид частных решений ЛНДУ, используя метод неопределенных коэффициентов (числовые значения коэффициентов не находить).

1. у″-3у′+2у =f(х), а) f(х) = x+2е^х;

б) f(х)=3cos4x;

в) f(х)= 4xе^-х+7.

2. у″-у′= f(х), а) f(х) = x⁴+х³-7х ;

б) f(х)= е^хsin2x+3х²;

в) f(х)= 6хcosx-хsinx.

3. у″+у′-2у= f(х), а) f(х) = е^хsin3х+6х³;

б) f(х)= х²е^-2х +sinx ;

в) f(х)= cos2x-е^-2х.

ІV. Решить ЛНДУ, применяя метод неопределенных коэффициентов.

1) у″+6у′ +9у =10sinx; 2) у″-6у′ +9у =16е^-х.

V. Решить лнду двумя способами:

а) методом неопределенных коэффициентов;

б) методом вариации произвольных постоянных.

у″+9у=36е^3х, у(0)=2, у′(0)=6.

Типовой расчет по теме «Дифференциальные уравнения второго порядка» Вариант 8

І. Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами.

1) у″+6у′+9у=0; 3) у″+3у′=0;

2) у″+2у′+5у=0; 4) у″′-у′=0.

ІІ. Применяя метод вариации произвольных постоянных, решить ЛНДУ:

1) у″+у=4x² ; 2) у″+ 16у= .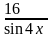

ІІІ. Указать вид частных решений ЛНДУ, используя метод неопределенных коэффициентов (числовые значения коэффициентов не находить).

1. у″-4у′+4у=f(х), а) f(х) =sin2x+2е^х;

б) f(х)= x²-4;

в) f(х)= х· sin3x.

2. у″+9у= f(х), а) f(х) = x²е^3х+2х;

б) f(х)= е^хsin3x-cos3x;

в) f(х)= (х²-4x+1)е^-х .

3. у″+2у′+2у= f(х), а) f(х) = x³е^2хsinx-е^2хcosx;

б) f(х)= 5sinx-7х⁵;

в) f(х)= 4е^-х · cosx.

ІV. Решить ЛНДУ, применяя метод неопределенных коэффициентов.

1) у″+4у′= е^-2х; 2) у″-у′= 3(2-x²).

V. Решить лнду двумя способами:

а) методом неопределенных коэффициентов;

б) методом вариации произвольных постоянных.

у″+3у′= 3xе^-3х , у(0)=3, у′(0)=-1.

Типовой расчет по теме «Дифференциальные уравнения второго порядка» Вариант 9

І. Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами.

1) у″-6у′+9у=0; 3) у″-2у′=0;

2) у″+9у=0; 4) у^ІV -8у″+16у =0.

ІІ. Применяя метод вариации произвольных постоянных, решить ЛНДУ:

1) у″-7у′+6у=sinx; 2) у″+у=4ctgx.

ІІІ. Указать вид частных решений ЛНДУ, используя метод неопределенных коэффициентов (числовые значения коэффициентов не находить).

1. у″-у′+у=f(х), а) f(х) = е^хcosx;

б) f(х)= 7x+2+е^-3х;

в) f(х)= x²sin4x.

2. 3у″-2у′-8у = f(х), а) f(х) = x⁴+х+1;

б) f(х)= е sin5x-7x;

в) f(х)= е^2х(х-4).

3. у″+4у′+29у= f(х), а) f(х) = 12x²е^4х-8cos5x;

б) f(х)= 6е^-2хsin5x;

в) f(х)= 2хcos3x-6х³sin3x.

ІV. Решить ЛНДУ, применяя метод неопределенных коэффициентов.

1) у″-4у′+5у=2х²е^х 2) 7у″-у′= 14x.