6.8. Вычисление длины дуги плоской кривой

Прямоугольные координаты

Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у = f(x), где а  х  b.

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у = f(x) и ее производная y = f(x) непрерывны на отрезке [а, b], то кривая АВ имеет длину, равную

(6.14)

или в сокращённой записи

.

Если уравнение кривой АВ задано в параметрической форме

  t  ,

где x(t) и y(t) – непрерывные функции с непрерывными производными и x() = а, x() = b, то длина l кривой АВ находится по формуле

. (6.15)

Пример. Найти длину окружности радиуса R.

Решение.

Найдем часть ее длины от точки (0; R) до точки (R; 0) (рис. 6.13). Так как , то

.

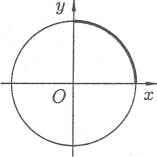
Рис. 6.13

Значит, l = 2 R. Если уравнение окружности записать в параметрическом виде х = R cos t, у = R sin t (0  t  2), то

.

Полярные координаты

Пусть кривая АВ задана уравнением в полярных координатах r = r(),     . Предположим, что r() и r'() непрерывны на отрезке [, ].

Если в равенствах х = r cos, у = r sin, связывающих полярные и декартовы координаты, параметром считать угол , то кривую АВ можно задать параметрически

Применяя формулу (6.15), получаем .

Пример. Найти длину кардиоиды r = a (1 + cos).

Решение.

Кардиоида r = a (1 + cos) имеет вид, изображенный на рисунке 6.14. Она симметрична относительно полярной оси. Найдем половину длины кардиоиды:

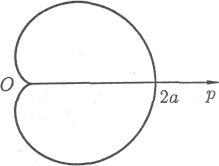
Рис. 6.14.

Таким образом, . Значит, l = 8а.

6.9. Вычисление объемов тел

Вычисление объема тела по известным площадям параллельных сечений

Если известны площади S сечений какого-либо тела плоскостями, перпендикулярными некоторой оси, например оси Ox: S = S(x), а  х  b, то объем V этого тела можно найти по формуле

. (6.16)

Данная формула называется формулой объема тела по площади параллельных сечений.

Пример. Найти объем эллипсоида .

Решение.

Рассекая эллипсоид плоскостью, параллельной плоскости Oyz и на расстоянии х от нее (-а  х  а), получим эллипс (см. рис. 15):

.

Площадь этого эллипса равна

.

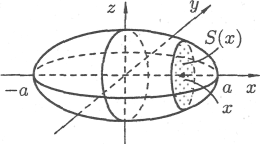
Рис. 6.15.

Поэтому, по формуле (6.16), имеем

.

Объем тела вращения

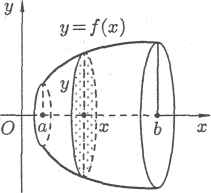
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = f(x)  0, отрезком а  х  b и прямыми х = а и х = b (см. рис. 16). Полученная от вращения фигура называется телом вращения.

Рис. 6.16.

Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х  [а, b]), есть круг с радиусом у = f(x). Следовательно, S(х) =  у². Применяя формулу (16) объема тела по площади параллельных сечений, получаем

. (6.17)

Если криволинейная трапеция ограничена графиком непрерывной функции х = (у)  0 и прямыми х = 0, у = с, у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (6.17), равен

. (6.18)

Пример. Найти объем тела, образованного вращением фигуры,

Рис. 6.17.

ограниченной линиями , х = 0, вокруг оси Оу (рис. 6.17).

Решение:

По формуле (6.18) находим:

.