4.14. Производная в данном направлении и градиент функции

Производной функции z=f(x,y) в данном направлении называется , где и — значения функции в точках и . Если функция z дифференцируема, то справедлива формула

, (4.13)

где - угол, образованный вектором l с осью ОХ.

Аналогично определяется производная в данном направлении l для функции трех аргументов u=f (x,y,z). В этом случае

, (4.14)

где — углы между направлением l и соответствующими координатными осями. Производная в данном направлении характеризует скорость изменения функции в этом направлении.

Пример 1. Найти производную функции z = 2х² — Зу² в точке P(1; 0) в направлении, составляющем с осью ОХ угол в 120°.

Решение. Найдем частные производные данной функции и их значения в точке P:

Здесь cos = cos 120º = - ½,

sin = sin 120º = .

Применяя формулу, получим:

.

Знак минус показывает, что функции в данной точке и в данном направлении убывает.

Градиентом функции z=f (x,y) называется вектор, проекциями которого на координатные оси являются соответствующие частные производные данной функции:

. (4.15)

Производная данной функции в направлении l связана с градиентом функции формулой , т. е. производная в данном направлении равна проекции градиента функции на направление дифференцирования.

Градиент функции в каждой точке направлен по нормали к соответствующей линии уровня функции. Направление градиента функции в данной точке есть направление наибольшей скорости возрастания функции в этой точке, т. е. при l=grad z производная принимает наибольшее значение, равное .

Аналогично определяется градиент функции трех переменных u=f(x,y,z):

. (4.16)

Градиент функции трех переменных в каждой точке направлен по нормали к поверхности уровня, проходящей через эту точку.

Пример. Найти градиент функции z=x²y в точке Р(1;1).

Решение. Вычислим частные производные и их значения в точке Р.

Следовательно, grad z=2i+j .

4.15. Экстремум функции нескольких переменных. Условный экстремум. Наибольшее и наименьшее значения функции

Определение экстремума функции

Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной.

Пусть функция z = f(x; у) определена в некоторой области D, точка N(x₀;y₀) D.

Точка (x₀;y₀) называется точкой максимума функции z= f(x;y), если существует такая -окрестность точки (x₀;y₀), что для каждой точки (х;у), отличной от (x₀;y₀) из этой окрестности выполняется неравенство f(x;y)<f(x₀;y₀). На рисунке 4.17: N₁ — точка максимума, a N₂ — точка минимума функции z= f(x;y).

Рис. 4.17

Аналогично определяется точка минимума функции: для всех точек (x₀;y₀),отличных от (x₀;y₀),из -окрестности точки (x₀;y₀) выполняется неравенство: f(x₀;y₀) > f(x₀;y₀) .

Аналогично определяется экстремум функции трех и большего числа переменных.

Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции.

Максимум и минимум функции называют её экстремумами.

Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке (x₀;y₀) сравнивается с ее значениями в точках, достаточно близких к (x₀;y₀) . В области D функция может иметь несколько экстремумов или не иметь ни одного.

Необходимые условия экстремума

Рассмотрим условия существования экстремума функции.

Геометрически равенства f'_y(x₀;y₀) = 0 и f'_y(x₀;y₀) = 0 означают, что в точке экстремума функции z = f(x; у) касательная плоскость к поверх­ности, изображающей функцию f(x; у), параллельна плоскости О_ху, т. к. уравнение касательной плоскости есть z = z₀ .

Замечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функция имеет максимум в точке О(0;0), но не имеет в этой точке частных производных.

Точка, в которой частные производные первого порядка функции z = f(x;y) равны нулю, т. е. f'_x = 0, f'_y = 0, называется стационарной точкой функции z.

Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.

В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию z = ху. Для нее точка О(0; 0) является критической (в ней и обращаются в ноль). Однако экстремума в ней функция z = ху не имеет, т. к. в достаточно малой окрестности точки О(0;0) найдутся точки для которых z > 0 (точки I и III четвертей) и z < 0 (точки II и IV четвертей).

Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.

Стационарные точки находятся путем решения системы уравнений

f_х (х, у) = 0, f'_у(х,у) = 0 (4.17)

(необходимые условия экстремума).

Система (1) эквивалентна одному уравнению df(х, у)=0. В общем случае в точке экстремума Р(а, b) функции f(x, у) или df(x, y)=0, или df(а, b) не существует.

Достаточные условия экстремума

Пусть Р(а; b) — стационарная точка функции f(х,у), т. е. df(а, b) = 0. Тогда:

а) если d²f (а, b) < 0 при , то f(а, b) есть максимум функции f (х, у);

б) если d²f (а, b) > 0 при , то f(а, b)есть минимум функции f (х,у);

в) если d²f (а, b) меняет знак, то f (а, b) не является экстремумом функции f (х, у).

Приведенные условия эквивалентны следующим: пусть и . Составим дискриминант Δ=AC — B².

Тогда:

1) если Δ > 0, то функция имеет экстремум в точке Р (а; b) а именно максимум, если A<0 (или С<0), и минимум, если A>0 (или С>0);

2) если Δ < 0, то экстремума в точке Р(а; b) нет;

3) если Δ=0, то вопрос о наличии экстремума функции в точке Р(а; b) остается открытым (требуется дальнейшее исследование).

Пример. Исследовать на экстремум функцию z=x³+3xy²-15x-12y.

Решение. Найдем частные производные и составим систему уравнений:

или

Решая систему, получим четыре стационарные точки:

Найдем производные 2-го порядка

и составим дискриминант Δ=AC — B² для каждой стационарной точки.

1) Для точки : , Δ=AC—B²=36-144<0. Значит в точке экстремума нет.

2) Для точки P₂: А=12, B=6, С=12; Δ=144-36>0, A>0. В точке Р₂ функция имеет минимум. Минимум этот равен значению функции при х=2, у=1: zmin=8+6-30-12=-28.

3) Для точки : A= -6, B=-12, С= -6; Δ = 36-144 <0. Экстремума нет.

4) Для точки Р₄: A=-12, B=-6, С=-12; Δ=144-36>0. B точке Р₄ функция имеет максимум, равный Z_mах=-8-6+30+12=28.

Условный экстремум

В простейшем случае условным экстремумом функции f(х,y) называется максимум или минимум этой функции, достигнутый при условии, что ее аргументы связаны уравнением φ(х,у)=0. Чтобы найти условный экстремум функции f(х, у) при наличии соотношения φ(х,у) = 0, составляют так называемую функцию Лагранжа

F(x,y)=f(x,y)+ λφ(x,y),

где λ — неопределенный постоянный множитель, и ищут обычный экстремум этой вспомогательной функции. Необходимые условия экстремума сводятся к системе трех уравнений

(4.18)

с тремя неизвестными х, у, λ, из которой можно, вообще говоря, определить эти неизвестные.

Вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала функции Лагранжа

для испытуемой системы значений х, у, λ, полученной из (4.18) при условии, что dх и dу связаны уравнением

.

Именно, функция f(х,y) имеет условный максимум, если d²F< 0, и условный минимум, если d²F>0. В частности, если дискриминант Δ для функции F(х,у} в стационарной точке положителен, то в этой точке имеется условный максимум функции f(х, у), если A< 0 (или С< 0), и условный минимум, если А > О (или С>0).

Аналогично находится условный экстремум функции трех или большего числа переменных при наличии одного или нескольких уравнений связи (число которых, однако, должно быть меньше числа переменных). Здесь приходится вводить в функцию Лагранжа столько неопределенных множителей, сколько имеется уравнений связи.

Пример. Найти экстремум функции z=6-4x-3y при условии, что переменные х и у удовлетворяют уравнению x²+y²=1.

Решение. Геометрически задача сводится к нахождению наибольшего и наименьшего значений аппликаты z плоскости z=6 - 4х - Зу для точек пересечения ее с цилиндром х²+у²=1.

Составляем функцию Лагранжа F(x,y)=6 -4x -3y+λ(x²+y² -1).

Имеем . Необходимые условия дают систему уравнений

решая которую найдем:

и

.

Так как

,

то

d²F=2λ(dx²+dy²).

Если и , то d²F>0, и, следовательно, в этой точке функция имеет условный минимум. Если и , то d²F<0, и, следовательно, в этой точке функция имеет условный максимум.

Таким образом,

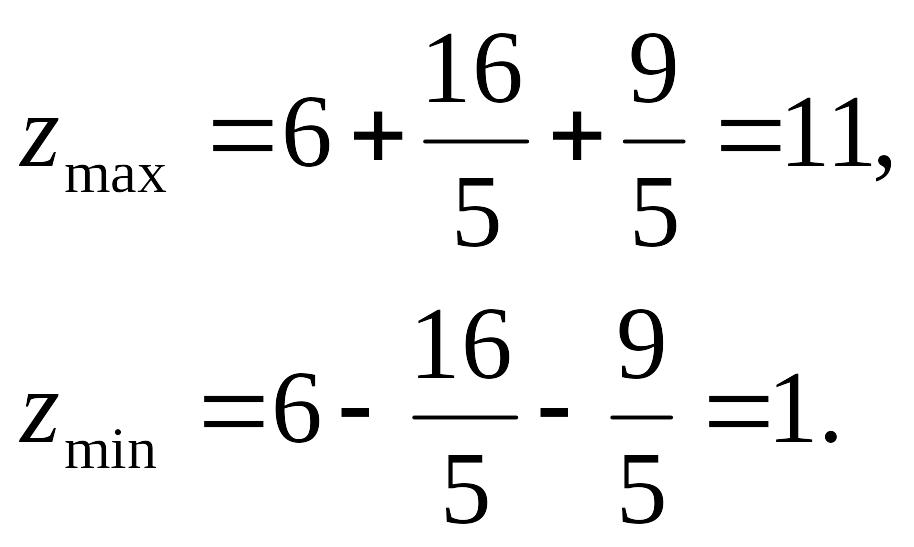
Наибольшее и наименьшее значения функции

Пусть функция z = f(x; у) определена и непрерывна в ограниченной замкнутой области . Тогда она достигает в некоторых точках своего наибольшего М и наименьшего т значений. Эти значения достигаются функцией в точках, расположенных внутри области , или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значений дифференцируемой в области функции z = f(x;y) состоит в следующем:

1. Найти все критические точки функции, принадлежащие , и вычислить значения функции в них;

2. Найти наибольшее и наименьшее значения функции z = f(x; у) на границах области;

3. Сравнить все найденные значения функции и выбрать из них наибольшее М и наименьшее т.

Пример. Определить наибольшее и наименьшее значения функции

z=x²+y² -xy+x+y

в области

.

Решение. Указанная область есть треугольник (рис. 4.18).

1. Найдем стационарные точки:

отсюда x= -1, y= -1; получаем точку М( -1; -1).

В точке М значение функции . Исследование на экстремум обязательно.

2) Исследуем функцию на границах области.

При х=0 имеем z=у²+у, и задача сводится к отысканию наибольшего и наименьшего значений этой функции одного аргумента на отрезке . Проведя исследование, найдем, что в точке (0; -3); в точке .

При у=0 имеем z=х²+х. Аналогично найдем, что в точке ( -3;0); в точке .

Рис. 4.18

При х+у= -3 или у= -3 –х будем иметь z=3х²+9х+6.

Аналогично найдем, что в точке ; и совпадает с и . На прямой х+у = -3 можно было бы исследовать функцию на условный экстремум, не приводя к функции одного аргумента.

3) Сопоставляя все полученные значения функции z, заключаем, что в точках (0; -3) и ( -3; 0); в стационарной точке М.

42