4.12. Экономический смысл производной

Рассмотрим издержки производства y как функцию количества выпускаемой продукции х. Пусть - прирост продукции, тогда - среднее приращение издержек производства на единицу продукции. Производная выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.

Предельные издержки зависят от уровня производства (количества выпускаемой продукции) х и определяются не постоянными производственными затратами, а лишь переменными (на сырье, топливо и т.п.). Аналогичным образом могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность, предельная производительность и другие предельные величины.

Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности.

Эластичностью функции называется предел отношения относительного приращения функции у к относительному приращению переменной х при →0:

.

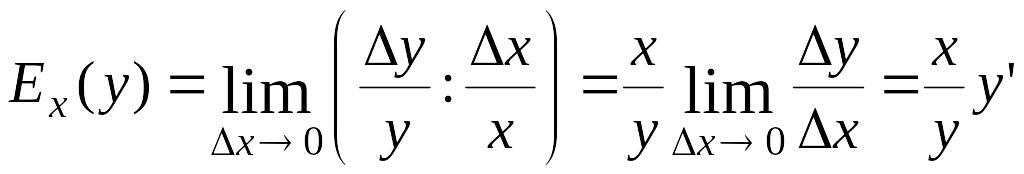Эластичность функции показывает приближенно, на сколько процентов изменится функция y=f(x) при изменении независимой переменной х на 1%.

Пример. Зависимость между себестоимостью единицы продукции у (тыс.руб.) и выпуском продукции х (млрд.руб.) выражается функцией . Найти эластичность себестоимости при выпуске продукции, равном 60 млн.руб.

Решение. Согласно определению эластичности имеем:

.

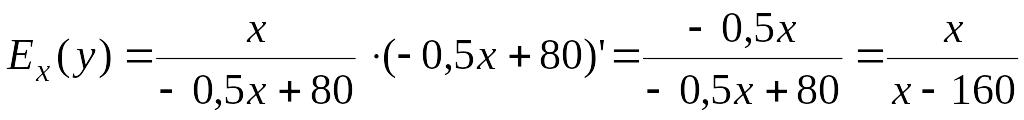При х=60 эластичность , т.е. при выпуске продукции, равном 60 млн.руб., увеличение его на 1% приведет к снижению себестоимости на 0,6%.

4.13. Дифференциальное исчисление функции многих переменных. Основные понятия

Понятие функции нескольких переменных

Пусть задано множество D упорядоченных пар чисел (х;у). Соответствие f, которое каждой паре чисел (x; у) D сопоставляет одно и только одно число z R , называется функцией двух переменных, определенной на множестве D со значениями в R, и записывается в виде

z =f(х; у)

При этом х и у называются независимыми переменными (аргументами), а z — зависимой переменной (функцией).

Аналогично определяются функции трех и большего числа аргументов. Множество D=D(f) называется областью определения функции. Множество значений, принимаемых z в области определения, называется областью изменения этой функции, обозначается Е(f) или Е.

Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило, аналитическим способом, когда функция задается с помощью формулы.

Примером функции двух переменных может служить площадь S прямоугольника со сторонами, длины которых равны х и у: S == ху.

Свойства функций, непрерывных в ограниченной замкнутой области

Приведем свойства функций, непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной). Предварительно уточним понятие области.

Областью называется множество точек плоскости, обладающих свойствами открытости и связности.

Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.

Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.

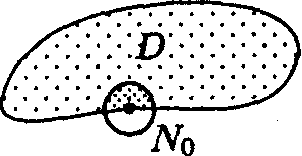
Рис. 4.15

Точка N₀ называется граничной точкой области D, если она не принадлежит D, но в любой окрестности ее лежат точки этой области (рис. 4.15). Совокупность граничных точек области D называется границей D. Область D с присоединенной к ней границей называется замкнутой областью, обозначается . Область называется ограниченной, если все ее точки принадлежат некоторому кругу радиуса R. В противном случае область называется неограниченной.

Теорема. Если функция z = f (N) непрерывна в ограниченной замкнутой области, то она в этой области:

а) ограничена, т. е. существует такое число R > О, что для всех точек N в этой области выполняется неравенство |f (N)| < R;

б) имеет точки, в которых принимает наименьшее и наибольшее М значения;

в) принимает хотя бы в одной точке области любое численное значение, заключенное между и M.

Частные производные

Пусть задана функция z = f(х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение ; сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается . Итак,

= .

Аналогично получаем частное приращение z по у:

= .

Полное приращение функции z определяется равенством

= .

Если существует предел

,

то он называется частной производной функции z =f(х; у) в точке М(х; у) по переменной х и обозначается одним из символов:

Частные производные по x в точке М_о(x₀;y₀) обычно обозначают символом

(x₀;y₀).

Аналогично определяется и обозначается частная производная от z=f(x;у) по переменной у:

=

Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции f(х; у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).

Пример. Найти частные производные функции

Решение.

Геометрический смысл частных производных функции двух переменных

Графиком функции z = f(x;y) является некоторая поверхность. График функции z=f(х;у₀) есть линия пересечения этой поверхности с плоскостью у = у₀. Исходя из геометрического смысла производной для функции одной переменной, заключаем, что , где — угол между осью Ох и касательной, проведенной к кривой z=f(х;у₀) в точке Мо(х₀;у₀;f(х₀;у₀)) (рис. 4.16).

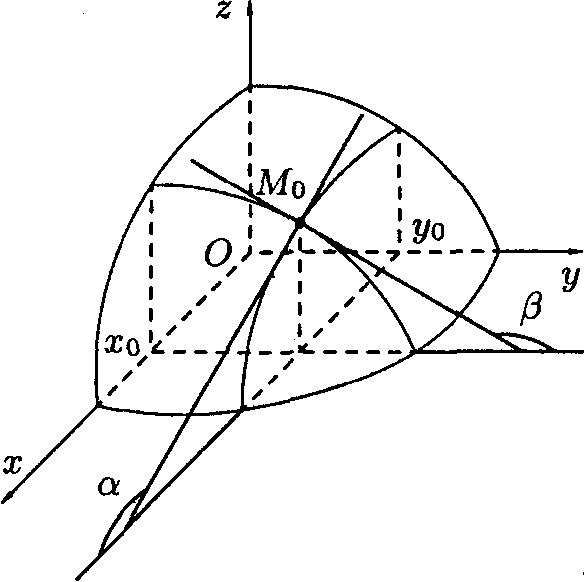
Рис. 4.16

Аналогично,

Частные производные высших порядков

Частные производные и называют частными производными первого порядка. Их можно рассматривать как функции от (x;y) D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:

Аналогично определяются частные производные 3-го, 4-го и т. д. порядков.

Так 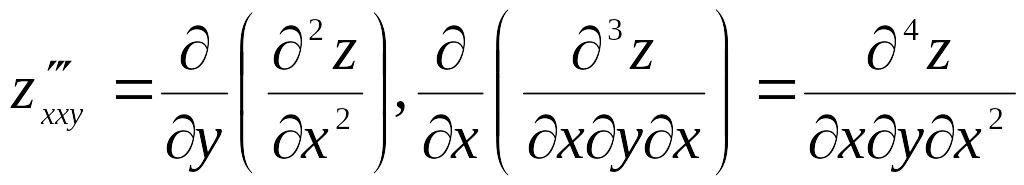(или ).

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Таковыми являются, например,

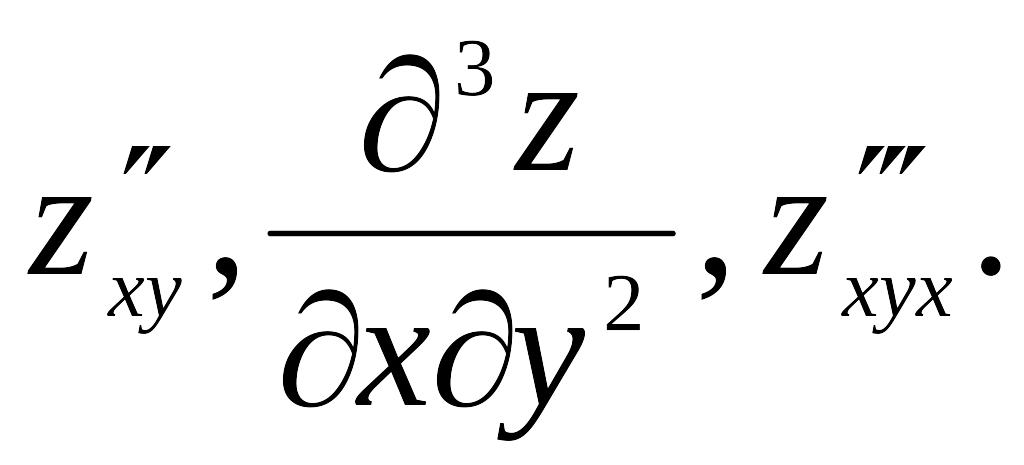
Пример. Найти частные производные второго порядка функции

z = х⁴ - 2х²у³ + у⁵ + 1.

Решение. Так как и , то

,

Оказалось, что

Этот результат не случаен. Имеет место теорема, которую приведем без доказательства.

Теорема Шварца. Если частные производные высшего порядка непрерыв­ны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.

В частности, для z = f(х;у) имеем:

Теорема (необходимое условие дифференцируемости функции). Если функция z = f(x; у) дифференцируема в точке М(х;у), то она непрерывна в этой точке, имеет в ней частные производные и , причем = А, = В.

Теорема (достаточное условие дифференцируемости функции). Если функция z=(x;у) имеет непрерывные частные производные и в точке М(х;у), то она дифференцируема в этой точке.

Чтобы функция z = f(х; у) была дифференцируема в точке, необходимо, чтобы она имела в ней частные производные, и достаточно, чтобы она имела в точке непрерывные частные производные.

Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциалов функции двух (и большего числа) переменных.

Функция заведомо имеет полный дифференциал в случае непрерывности ее частных производных. Если функция имеет полный дифференциал, то она называется дифференцируемой. Дифференциалы независимых переменных совпадают с их приращениями, т. е. dx=Δx и dy=Δy. Полный дифференциал функции z=f(x,y) вычисляется по формуле

.

Аналогично, полный дифференциал функции трех аргументов u=f(х, у, z) вычисляется по формуле

.