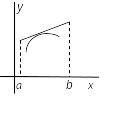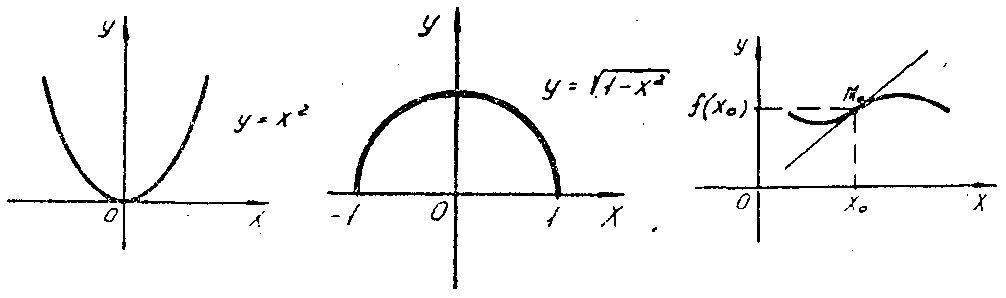4.11 Выпуклость и вогнутость графика функции. Точки перегиба. Асимптоты графика функции

Ещё одной важной характеристикой функции является характер её выпуклости.

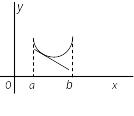
График дифференцируемой функции называется вогнутым в интервале (a,b), если он расположен выше любой своей касательной в этом интервале (рис. 4.10).

График дифференцируемой функции называют выпуклым в интервале (a, b), если он расположен ниже любой своей касательной в этом интервале (рис. 4.11).

Рис. 4.10.	Рис. 4.11

Так парабола у = х ² – функция вогнута на всей числовой оси (рис. 4.12), а полуокружность (рис. 4.13) имеет выпуклый график на отрезке [-1; 1].

Точка М₀ (x₀, f (x₀)), лежащая на графике и отделяющая выпуклую часть графика от вогнутой, называется точкой перегиба функции у = f (x) (рис. 14).

За выпуклость (вогнутость) функции "отвечает" вторая производная функции у = f (x).

Справедливо следующее утверждение: если функция у = f (x) имеет вторую производную f (x) во всех точках интервала (a, b) и если во всех точках этого интервала f (x) < 0. то график функции в интервале (a, b) – выпуклый, если же f (x) > 0, то график функции вогнутый в этом интервале.

Рис. 4.12	Рис. 4.13	Рис. 4.14

Точки перегиба следует искать среди тех точек, в которых вторая производная у = f (x) = 0.

Если слева от такой точки и справа от нее f  (x) имеет разные знаки, то найденная точка будет точкой перегиба.

Построение графика функции значительно облегчается, если знать его асимптоты.

Асимптотой кривой называется прямая, расстояние от которой до точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Асимптоты могут быть вертикальными, наклонными и горизонтальными.

Говорят, что прямая является вертикальной асимптотой графика функции y = f (x), если , или , или . То есть, для отыскания вертикальных асимптот следует найти те значения х, при которых функция обращается в бесконечность (терпит бесконечный разрыв).

Для определения наклонной асимптоты y = kx + b числа k (угловой коэффициент прямой) и b находят из формул:

, .

Но если хотя бы один из этих пределов не существует или равен бесконечности, то кривая y = f (x) наклонных асимптот не имеет.

Отметим, что следует отдельно рассмотреть случаи х +  и х   . Частным случаем наклонной асимптоты при k = 0 и будет горизонтальная асимптота. Поэтому y = b – уравнение горизонтальной асимптоты.

Если точка М (х, у) лежит на графике и неограниченно удаляется от начала координат, то она приближается к одной из этих прямых; расстояние от точки М (х, у) до асимптот стремится к нулю.

Общая схема исследования функции и построения графика

1. Для общего исследования функции и построения графика полезно придерживаться следующего плана. Найти область определения функции, точки разрыва функции и интервалы непрерывности

2. Найти (если это возможно) точки пересечения графика с осями координат.

3. Найти интервалы знакопостоянства функции (промежутки, на которых f (x) > 0 или f (x) < 0).

4. Решить вопрос о чётности, нечётности, симметрии, периодичности функции.

5. Если есть точки разрыва 2-го рода, найти вертикальные асимптоты.

6. Найти, если они есть, наклонные и горизонтальные асимптоты.

7. С помощью 1-ой производной найти точки экстремума и области возрастания и убывания данной функции. Найти экстремальные значения функции.

8. С помощью 2-ой производной найти точки перегиба, области выпуклости и вогнутости.

9. Построить график.