4.10 Экстремумы функций, наибольшее и наименьшее значения функции на отрезке

Если есть функция у = f (х), которая имеет конечную производную в каждой точке отрезка [а, b] (говорят, функция f (х) – дифференцируема на отрезке [а ,b] ), то её поведение можно исследовать с помощью производной y = f (x). Ранее мы отмечали, что интервалы возрастания и убывания f (x) определяются знаком f  (x).

Как видно из рис. 4.8, такими точками являются точки х₁, х₂, х₃, х₄. Точка х₁, например, обладает следующим свойством: значение функции в точке х₁ больше значений функции во всех «соседних» точках как слева, так и справа от х₁.

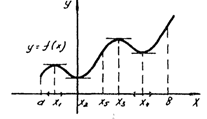
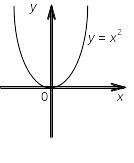
Рис 4.8. Рис. 4.9.

В этом случае говорят, что функция имеет в точке х₁ максимум. В точке х₃ функция тоже имеет максимум, а сами точки х = х₁ и х = х₃ называют точками максимума. И хотя значение функции в точке максимума х₁ меньше, чем, например, в точке х₅, важно отметить, что «по – соседству» с х₁ имеем f (x) < f (x₁). Говорят, что функция у = f (х) имеет максимум (max) в точке х = с, если существует такая окрестность точки х = с, что для всех точек х  с, принадлежащих этой окрестности, выполняется неравенство f (x) < f (с).

Функция у = f (х) имеет минимум (min) в точке х = с, если существует такая окрестность точки х = с, что для всех точек х  с, принадлежащих этой окрестности, выполняется неравенство f (x) > f (с).

Таким свойством, очевидно, обладают точки х = х₂ и х = х₄, эти точки называют точками минимума. Точки максимума и минимума объединяют под общим названием точки экстремума.

Точки экстремума лежат внутри области определения функции, их ещё называют локальный максимум и локальный минимум (от латинского слова lokal – местный). Точки же х = b и х = х₂ на рис. 4.8 являются глобальным максимумом и глобальным минимумом, или, говорят, наибольшим и наименьшим значением f (x) на замкнутом интервале [a, b]. В нашем случае глобальный максимум совпадает с концом интервала х = b, а глобальный минимум совпадает с локальным в точке х = х₂. Функция, непрерывная на замкнутом интервале, достигает своего наибольшего и наименьшего значения.

Что можно сказать о производной в точках экстремума? (Мы рассматриваем случай, когда производная существует во всех точках [a, b].)

Вспомним, что производная f (x₀) связана с касательной, проведённой в точке х₀. В точках экстремума х₁, х₂, х₃, х₄ (т.е. на «вершинах» и на «дне оврагов») касательные горизонтальны, т.е. f (x₁) = f (x₂) = f (x₃) = f (x₄) = 0.

Сформулируем необходимый признак существования экстремума.

Теорема (необходимый признак существования экстремума). Если f (x) имеет в точке х = с экстремум и дифференцируема в этой точке, то f (с) = 0.

Не следует думать, что верно и обратное утверждение. Из того, что f  (с) = 0 ещё не следует, что точка х = с является точкой минимума или максимума.

На рис. 4.9 изображен график функции у = х ³. В точке х = 0 касательная горизонтальна и производная равна нулю, но в этой точке у функции нет ни минимума, ни максимума. Из сказанного следует, что обращение в нуль производной в точке, еще не достаточно, чтобы утверждать, что в этой точке экстремум. Однако, искать точки экстремума следует среди тех, в которых производная равна нулю.

Такие точки называют стационарными.

Чем же отличается, например, точка х₃ на рис. 4.8 от точки х = 0 на рис. 4.9?

И в той, и в другой точке касательные параллельны оси Ох, т.е. f = 0, обе точки стационарные.

В точке х = х₃ (рис. 4.8) функция f (х) меняет характер монотонности (с возрастания на убывание), т.е. производная слева от х₃ положительна, а справа – отрицательна.

В точке х = 0 (рис. 4.9) функция у = х ³ характер монотонности не меняет, слева и справа от стационарной точки функция возрастает и её производная = 3 х ² сохраняет положительный знак.

Теорема (достаточный признак существования экстремума). Если непрерывная функция у = f (х) имеет производную f (х) во всех точках некоторого интервала, содержащего стационарную точку х = с, и если производная f (х) при переходе аргумента слева направо через стационарную точку х = с меняет знак с «плюса» на «минус», то стационарная точка х = с есть точка максимума, а при перемене знака с «минуса» на «плюс» – точка минимума.

Пример. Определить экстремум функции у = х ³ – Зх ² +2 и найти её наименьшее и наибольшее значение на отрезке [-0,5; 4].

Решение. Областью существования функции является вся числовая ось (; ). Находим производную у '(х) = З х ² - 6х. Приравниваем производную нулю, находим стационарные точки: 3 х ² – 6 х = 3 х (х - 2) = 0. Решаем это уравнение и получаем х₁ = 0, х₂ = 2. Нанесём наши точки на числовую ось и посмотрим как ведёт себя производная у ' (х) = 3х (х - 2) на отрезке [-0,5; 4].

Рассмотрим интервалы (-0,5; 0), (0; 2), (2; 4).

На интервале (-0,5; 0) производная f  (х) > 0, на интервале (0; 2) производная f  (х) < 0. (Убедиться в этом можно, подставляя в производную какую-нибудь точку из рассматриваемых интервалов). Теперь рассмотрим интервал (2; 4) и убедимся, что f (х) > 0. Таким образом, переходя через точку х = 0, производная меняет знак с «плюса» на «минус», т.е. стационарная точка х=0 является точкой максимума, а в точке х = 2 происходит смена знака производной с «минуса» на «плюс» и х = 2 – точка минимума. Значение функции в точках х_min и х_max вычислим, подставив х = 2 и х = 0 в уравнение у = х ³ – 3х ² + 2.

Получим, х_max = 0, у_max = у(0) = 2; х_min = 2, у_min = у(2) = – 2.

Итак, мы определили локальные экстремумы.

Чтобы найти наибольшее и наименьшее значения функции – глобальные экстремумы – применяется следующее правило:

1. Находим все стационарные точки и точки, в которых производная не существует, вычисляем в них значения функции.

2. Вычисляем значения функции на концах отрезка, в точках х = а, х = b.

3. Сравнивая между собой вычисленные значения функции, выбираем наибольшее и наименьшее.

Так как значения в стационарных точках вычислены, подсчитаем значения функции на концах отрезка [-0,5; 4], в точках х = 0,5; х = 4.

у(0,5)=( 0,5) ³  3 ( 0,5)² + 2 = + ; у (4 ) = 4 ³  34 ² + 2 = 18

Сравниваем значения функции у (-0,5), у (0), у (2), у (4), получаем, что наибольшее значение достигается на правом конце у (4)^:=18, а наименьшее в точке локального минимума у (2) = 2.