4.8. Правила Лопиталя

Правила Лопиталя применяются для раскрытия неопределённостей вида и , которые называются основными.

Теорема. (Правило Лопиталя раскрытия неопределённостей вида ).

Пусть функции f (x) и g (x) непрерывны и дифференцируемы в окрестности точки х₀ и обращаются в нуль в этой точке: f (x₀) = g (x₀) = 0. Пусть g (x)  0 в окрестности точки x₀. Если существует предел , то .

Пример. Найти .

Решение. .

Теорема. (Правило Лопиталя раскрытия неопределённостей вида ).

Пусть функции f (x) и g (x) непрерывны и дифференцируемы в окрестности точки х₀ (кроме, может быть, точки х₀), в этой окрестности , g (x)  0. Если существует предел , то .

Пример. Найти

Решение.

.

Неопределённости вида [0], [  ], [1^], [ ⁰], [0 ⁰] сводятся к двум основным путём тождественных преобразований.

1. Пусть f (x)  0, и g (x)  0 при х  х₀. Тогда очевидны следующие преобразования:

(или ).

Пример. Найти .

Решение.

.

2. Пусть f (x)  , и g (x)   при х  х₀. Тогда можно поступить так:

.

Пример. Найти .

Решение.

.

3. Пусть f (x)  1, и g (x)  , или f (x)  , и g (x)  0, или f (x)  0, и g (x)  0 при х  х₀. Для нахождения предела вида вспомним свойство логарифма .

Пример. Найти .

Решение. = = = = = = [tg 2x  2x] == = .

4.9. Возрастание и убывание функций

Одним из приложений производной является её применение к исследованию функций и построению графика функции.

Установим необходимые и достаточные условия возрастания и убывания функции.

Теорема (необходимые условия). Если дифференцируемая на интервале (a; b) функция f (x) возрастает (убывает), то f  (x)  0 (f  (x)  0) для любого х  (a; b).

Теорема (достаточные условия). Если функция f (x) дифференцируема на интервале (a; b) и f  (x) > 0 (f  (x) < 0) для любого х  (a; b), то эта функция возрастает (убывает) на интервале (a; b).

Посмотрим на графики функций y = f (x), y = g (x) и y =  (x), изображённые на рис. 4.3 – 4.5.

Функции f (x) и g (x) возрастают, но график, изображённый на рис. 4.3, пологий на участке [а, 0], т.е. функция y = f (x) меняется (растёт) медленно, график же функции g (x) круто поднимается вверх на участке , т.е. g (x) меняется (тоже растёт) быстро, с большей скоростью. Проведём касательные к нашим графикам в точке М₀.

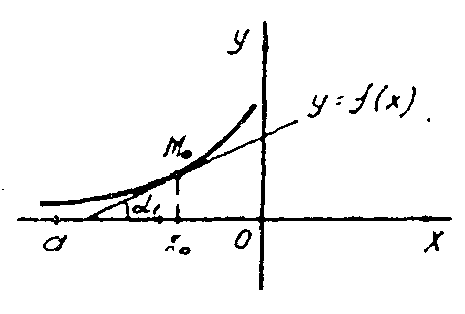
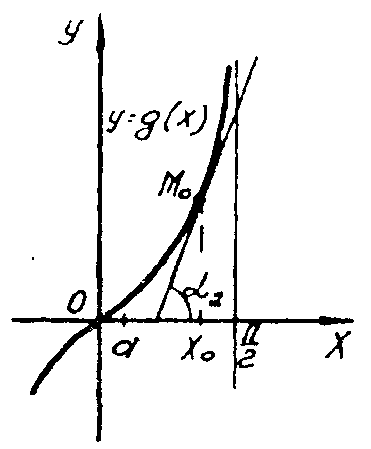
Рис. 4.3. Рис. 4.4

Сравним углы ₁ и ₂, которые образуют касательные к графикам с положительным направлением оси Ох. Так как углы ₁ и ₂ острые, то tg ₁ и tg ₂ положительны и по смыслу производной это обозначает, что обе функции возрастают в интервале от (a; x₀). Поскольку f (x₀)  g (x₀), график второй функции “круче”, чем график первой.

Эти рисунки отражают общее явление: если функция возрастает на интервале и имеет производную в каждой точке этого интервала, то производная неотрицательна; если производная положительна во всех точках интервала, то функция строго возрастает на этом интервале.

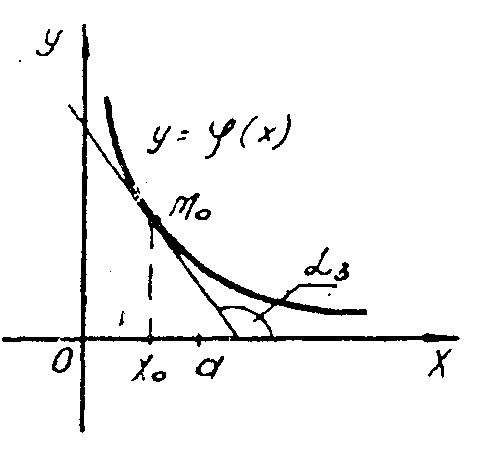
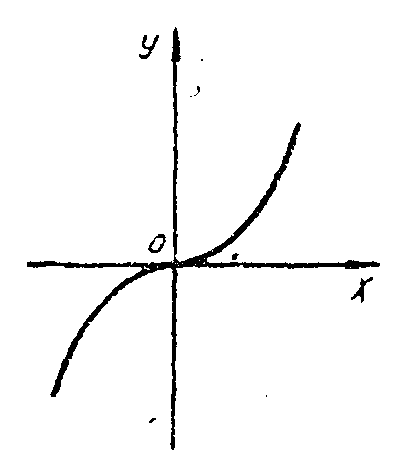
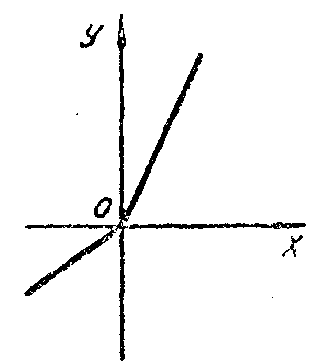
Рис. 4.5 Рис. 4.6. Рис. 4.7

Рассмотрим теперь рис. 4.5. На нём изображён график убывающей на [х₀, а] функции y =  (x). Угол ₃ касательной с осью Ох тупой и tg  ₃ =   (x₀)  0.

Этот рисунок отражает следующее общее явление: если функция убывает на интервале, то во всех точках этого интервала её производная не положительна; если производная отрицательна, то функция строго убывает.

В сформулированных утверждениях следует строго различать необходимые и достаточные условия. Поясним это примерами.

Функция у = х ³ строго возрастает на всей вещественной оси (рис. 4.6). Для её производной имеем у = 3х ². В частности, у = 0 при х = 0. Это означает, что положительность производной является достаточным, но не является необходимым условием (строгого) возрастания. Кроме того, следует не упускать из вида, что на участках возрастания (убывания), строгого или нет, могут встречаться точки, в которых функция вообще не имеет производной. Простейший пример даёт функция у = 2х + х, график которой имеет вид (рис. 4.7):