4.6. Понятие дифференциала функции, его геометрический смысл. Основные теоремы о дифференциалах

Дифференциалом функции у = f (х) в точке х называется главная часть её приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df (x)):

dy = f  (x)x. (4.8)

Дифференциал dy называют также дифференциалом первого порядка. Найдём дифференциал независимой переменной х, т.е. дифференциал функции у = х.

Так как у' = х' = 1, то, согласно формуле (4.8), имеем dy = dx = x, т.е. дифференциал независимой переменной равен приращению этой переменной: dx = x.

Поэтому формулу (4.8) можно записать так:

dy = f  (x) dx, (4.9)

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Из формулы (4.9) следует равенство . Теперь обозначение производной можно рассматривать как отношение дифференциалов dy и dx.

Пример. Найти дифференциал функции . Вычислить dy при х = 0, dx = 0,1.

Решение. По формуле dy = f  (x) dx находим

.

Подставив х = 0 и dx = 0,1, получим .

Выясним геометрический смысл дифференциала.

Для этого проведём к графику функции у = f (х) в точке М (х; у) касательную МТ и рассмотрим ординату этой касательной для точки х + х (рис. 2).На рисунке АМ = х, АМ₁ = у. Из прямоугольного треугольника МАВ имеем:

tg  = , т.е. АВ= tg  х.

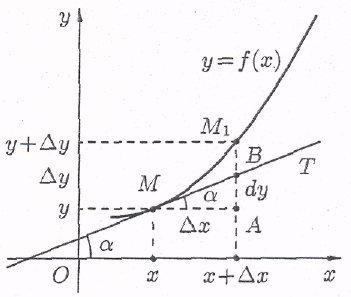
Рис. 4.2.

Но, согласно геометрическому смыслу производной, tg  = f  (х). Поэтому АВ = f  (х)х.

Сравнивая полученный результат с формулой (4.9), получаем dy = АВ, т.е. дифференциал функции у = f (х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение х.

Теорема. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:

d(u + v) = du + dv,

d(uv) = v du + u dv,

(v  0).

Теорема. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

dy = y_u  du.

Таблица дифференциалов

1. d(и ± v) = dи ± dv;

2. d(и  v) = vdи + udv, d(cu) = c du;

3. , ;

4. dу = у_х dx, если у = f (x);

5. dу = у_и  du, если у = f (и), и = (х);

6. dc = 0;

7. d (и ^ ) =  u ^–1  du;

8. d (а ^и ) = a ^u  ln a  du, d (e ^и ) = e ^u  du;

9. , ;

10. d (sin u) = cos u du;

11. d (cos u) = - sin u du;

12. d (tg u) = ;

13. d (ctg u) = ;

14. d (arcsin u) = ;

15. d (arcos u) = ;

16. d (arctg u) = ;

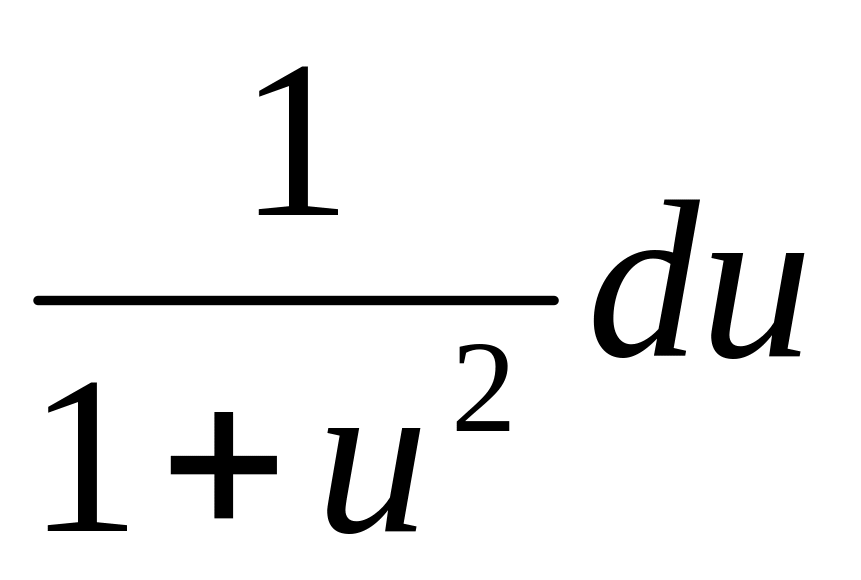17. d (arcctg u) = ;

18. d (sh u) = ch u du;

19. d (ch u) = sh u du;

20. d (th u) = ;

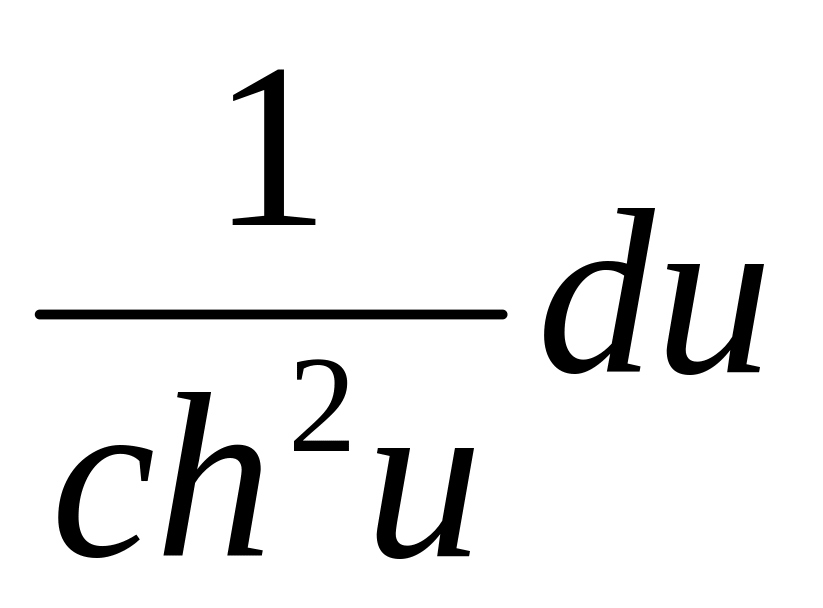21. d (cth u) = .

4.7. Применение дифференциала к приближённым вычислениям. Дифференциалы высших порядков

Приращение у функции у = f (х) в точке х можно представить в виде у = f  (х)  х, где   0 при х  0, или у = dy +   х. Отбрасывая бесконечно малую   х более высокого порядка, чем х, получаем приближённое равенство

y  dy, (4.10)

причём это равенство тем точнее, чем меньше х.

Это равенство позволяет с большой точностью вычислить приблизительно приращение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (4.10) широко применяется в вычислительной практике.

Подставляя в равенство (4.10) значения y и dy, получим

f (x₀+x)  f (x₀) + f  (x₀)x (4.11)

Пример. Вычислить приближённо агсtg (1,05).

Решение. Рассмотрим функцию f (х) = агсtg х. По формуле (4.11) имеем:

агсtg (x₀+x)  агсtg (х₀) + (агсtg (х₀))  x, т.е. агсtg (x₀+x) 

 агсtg (х₀) + .

Так как х = x₀ + x = 1,05, то при х₀ = 1 и x = 0,05 получаем:

aгсtg (1,05)  агсtg 1 + = + 0,025  0,810.

Пусть у = f (х) дифференцируемая функция, а её аргумент х- независимая переменная. Тогда её первый дифференциал dy = f (x) dx есть также функция от х; можно найти дифференциал этой функции.

Дифференциал от дифференциала функции у = f (х) называется её вторым дифференциалом (или дифференциалом второго порядка) и обозначается d ²y или d ² f (x):

d ² y = f  (x) dx ² (4.12)

Здесь dx ² обозначает (dx)².

Аналогично определяется и находится дифференциал третьего порядка:

d ³ y = d (d ² y) = d (f  (x) dx ² ) = f  (x) dx ³.

Вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)-го порядка: d ⁿ y = d (d ^{n - 1}y) = f ⁽ⁿ⁾ (x) (dx) ⁿ.

Отсюда находим, что . В частности, при n = 1, 2, 3 соответственно получаем: , , , т.е. производную функции можно рассматривать как отношение её дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Отметим, что все приведённые выше формулы справедливы только, если х – независимая переменная.

Пример. Найти d ² y, если y = e ^3x и х – независимая переменная.

Решение. Так как y = 3e ^3x, y = 9e ^3x, то по формуле (4.12) имеем d ²y = 9e ^3x dx ².