4.4. Логарифмическое дифференцирование

В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.

Пример. Найти производную функции у = .

Решение. Можно найти у' с помощью правил и формул дифференцирования. Однако такой способ слишком громоздкий. Применим логарифмическое дифференцирование. Логарифмируем функцию:

ln y = ln (x ² + 2) + ln (x - 1) + x – 3 ln (x + 5).

Дифференцируем это равенство по х:

.

Выражаем у': ,

т.е. .

Существуют функции, производные которых находят лишь логарифмическим дифференцированием. К их числу относится так называемая степенно-показательная функция у = и ^v, где и = и (х) и v = v (x) – заданные дифференцируемые функции от х. Найдём производную этой функции:

ln y = v  ln u  

 y = y(v ln u + v u), т.е. y= и ^v (v ln u + v u),

или

(u ^v) = u ^v ln uv+v u ^v-1 u. (4.5)

Сформулируем правило запоминания формулы (1.5): производная степенно-показательной функции равна сумме производной показательной функции, при условии и = const и производной степенной функции, при условии v= const.

Пример. Найти производную функции .

Решение. Пользуясь формулой (4.5), получаем:

.

Отметим, что запоминать формулу (4.5) необязательно, легче запомнить суть логарифмического дифференцирования.

4.5. Производные высших порядков

Производная у' = f (х) функции у = f (х) есть также функция от х и называется первой производной, или производной первого порядка.

Если функция f (х) дифференцируема, то её производная называется второй производной, или производной второго порядка и обозначается символами у, f (x) или .

Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у, f (x) или .

Вообще, производной n-го порядка функции f (х) называется первая производная от производной (n-1)-го порядка:

f ⁽ⁿ⁾ (x) = [f ^(n-1) (x)].

Пример. Найти значение третьей производной функции y = е ^5x+3 в точке x = 0.

Решение. Сначала найдём функцию y = (f(x) ), а затем вычислим её значение в точке x = 0.

y = (e^5x+3) = 5e^5x+3, y = (e^5x+3) = (5e^5x+3) = 25e^5x+3,

y = (25e^5x+3) = 125e^5x+3, y(0) = 125e^50+3 = 125e³.

Производные высших порядков неявно заданной функции

Пусть функция у = f (х) задана неявно в виде уравнения F (х; у) = 0.

Продифференцировав это уравнение по х и разрешив полученное уравнение относительно у', найдём производную первого порядка. Продифференцировав по х первую производную, получим вторую производную от неявной функции. В неё войдут х, у и у'. Подставляя уже найденное значение у' в выражение второй производной, выразим у" через х и у.

Аналогично поступаем для нахождения производной третьего (и дальше) порядка.

Пример. Найти у, если х ² + у ² = 1.

Решение. Дифференцируем уравнение х ² + у ² – 1 по х: 2 х + 2 уу' = 0.

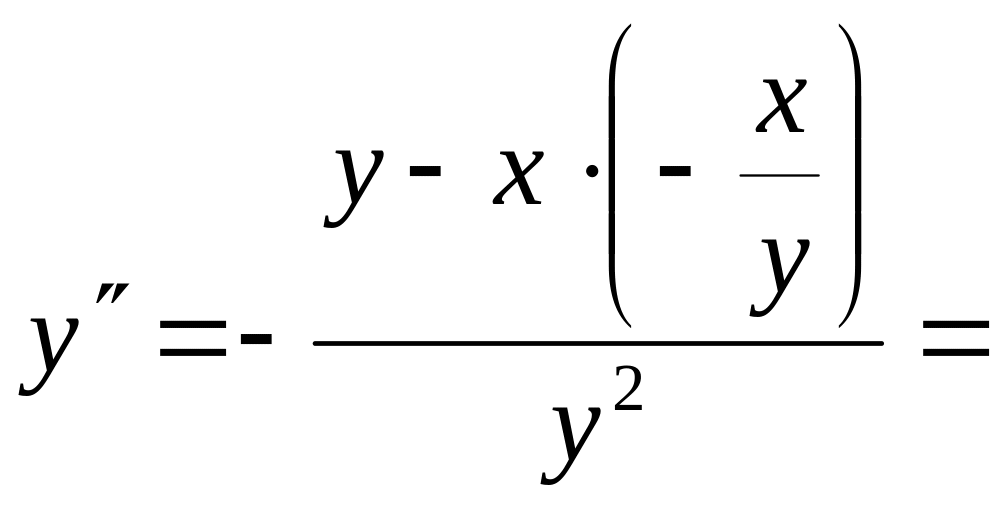
Отсюда . Далее имеем: , т.е. (так как х² + у² = 1),

следовательно, .

Производные высших порядков от функций, заданных параметрически

Пусть функция у = f (х) задана параметрическими уравнениями

Как известно, первая производная у'_х находится по формуле

. (4.6)

Найдём вторую производную от функции заданной параметрически. Из определения второй производной и равенства (4.6) следует, что

. (4.7)

Аналогично получаем , y ^V = , …

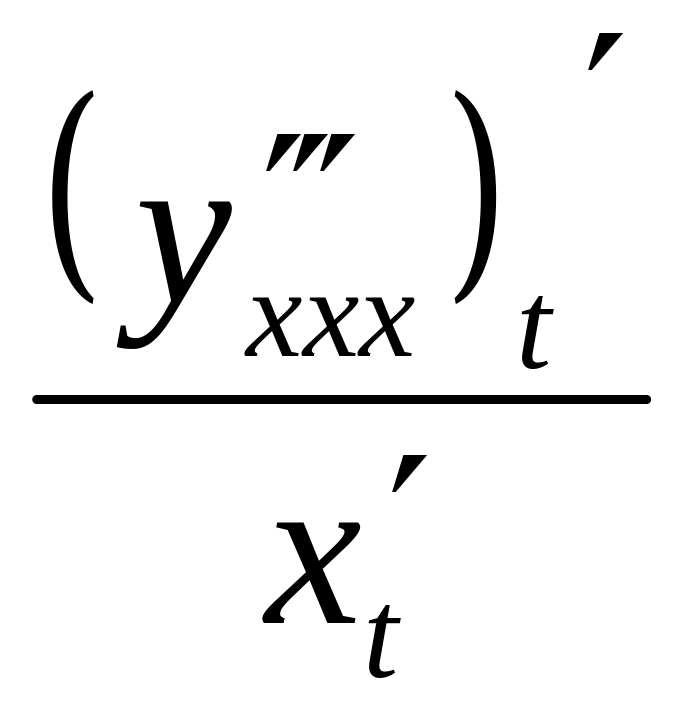Пример. Найти вторую производную функции

Решение. По формуле (4.6) ctg t.

Тогда по формуле (4.7) .