4.2. Основные правила дифференцирования

Если функции u = u (x) и v = v (x) дифференцируемы в точке x, тогда справедливы следующие правила дифференцирования:

1. (cu) = cu, где с – постоянная;

2. (u ± v)' = u' ± v';

3. (u v)' = u ' v – v ' u;

4. .

Пусть функция у = f (u), где u = u (х). Тогда у есть сложная функция от х: у = f (u (х)), а u – промежуточный аргумент. Чтобы найти производную этой сложной функции, применяют следующее правило:

, .

Например, если у = cos ³ х, то (см. таблицу основных формул дифференцирования), обозначив u = соs х, получим у = u ³.

Тогда у_x = 3u ²u_x; у_x = 3соs ² х (-sin х).

Таблица основных формул дифференцирования

На практике чаще всего приходится находить производные от сложных функций. Поэтому в приведённой ниже таблице формул дифференцирования используется промежуточный аргумент «и».

1. (c) = 0, с – постоянная.

2. (u ⁿ) = пu ^п1, ;

3. (а ^u) = а ^u ln a  u, y = e ^u, y = e ^u;

4. (log_a x) = , (ln u) = ;

5. (sin u) = cos u u;

6. (cos u)= sin u u;

7. (tg u)= ;

8. (ctg u)= .

9. (arcsin u) = ;

10. (arccos u) = ;

11. (arctg u) = ;

12. (arcctg u) = ;

13. (sh u) = ch u  u;

14. (ch u) = sh u  u;

15. (th u) = ;

16. (cth u) = .

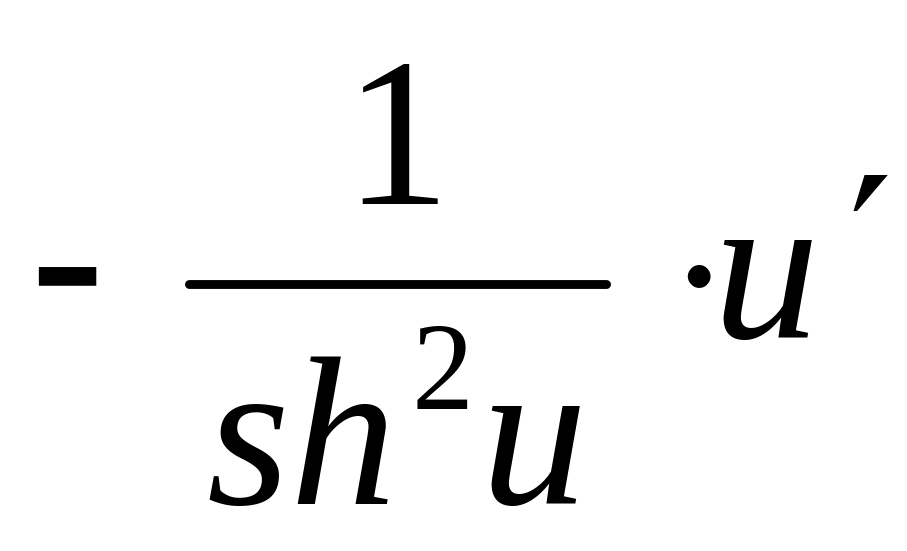Пример. Найти производную функции .

Решение.

=

= .

4.3. Дифференцирование функций, заданных неявно и параметрически

Если функция задана уравнением у = f (x), разрешённым относительно y, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F (х; у) = 0, не разрешённого относительно у.

Всякую явно заданную функцию у = f (x) можно записать как неявно заданную уравнением f (x) - у = 0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у + 2х + соs у - 1 = 0 или 2 ^y - х + у = 0).

Если неявная функция задана уравнением F (х; у) = 0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продиффиринцировать это уравнение по х, рассматривая при этом у как функцию от х и полученное затем уравнение разрешить относительно у.

Производная неявной функции выражается через аргумент х и функцию у.

Пример. Найти производную функции у, заданную уравнением х³ + у³ – 3ху = 0.

Решение. Функция у задана неявно. Дифференцируем по х равенство х ³ + у ³ – 3 х у = 0. Из полученного соотношения 3х ² + 3у ²у - 3 (1у + ху) = 0 следует, что у²у - ху = у - х ², т.е. .

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

(4.3)

где t – вспомогательная переменная, называемая параметром.

Найдём производную у'_х, считая, что функции (4.3) имеют производные и что функция х = х (t) имеет обратную t =  (x). По правилу дифференцирования обратной функции

. (4.4)

Функцию у = f (х), определяемую параметрическими уравнениями (4.3), можно рассматривать как сложную функцию у = y (t), где t =  (x). По правилу дифференцирования сложной функции имеем: у'_х = у_t  t_x. С учётом равенства (4.4) получаем

, т.е. .

Полученная формула позволяет находить производную у'_х от функции заданной параметрически, не находя непосредственной зависимости у от х.

Пример. Пусть Найти у'_х.

Решение. Имеем х'_t = 3 t ², у_t = 2 t. Следовательно, , т. е. .