3.4. Бесконечно малые и бесконечно большие функции. Свойства пределов

Функция y = f(x) называется бесконечно большой при х  а, где а – число или один из символов –, +, , если (или или ).

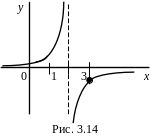
Например, функция является бесконечно большой при х  2 (но она не является бесконечно большой, например, при х  3) (рис. 3.14).

Функция является бесконечно большой при х   (но она не является бесконечно большой, например, при х  2) (рис. 3.15).

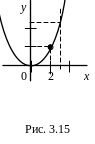
Функция y = f(x) (или последовательность {x_n}, поскольку числовая последовательность есть функция, определённая на множестве натуральных чисел) называется бесконечно малой при х  а, где а – число или один из символов –, +, , если (или ).

Например, функция у = х³ является бесконечно малой при х  0, т. к. ; функция у = sinх является бесконечно малой при х  , т. к.

 Если функция y = f(x) – бесконечно малая при х  а и f(x)  0 в некоторой окрестности точки а, то функция – бесконечно большая при х  а.

 Если функция y = f(x) – бесконечно большая при х  а, то функция – бесконечно малая при х  а.

Функция y = f(x) называется ограниченной в данном интервале, если существует число М > 0 такое, что для любого х, принадлежащего этому интервалу, выполняется условие f(x)  M. В противном случае функция y = f(x) называется неограниченной на интервале.

Например, функция ограничена в интервале (1, +), т. к. х  (1, +) имеет место (рис. 3.16). Эта же функция не ограничена в интервале (0, 1). Функция у = tgх ограничена в интервале и не ограничена в интервале (рис. 3.17).

Всякая постоянная величина является ограниченной функцией.

Свойства бесконечно малых

1. Сумма двух бесконечно малых является бесконечно малой.

2. Произведение бесконечно малой (х) при х  а на функцию и(х), ограниченную вблизи а, есть бесконечно малая при х  а.

3. Произведение двух бесконечно малых есть бесконечно малая.

4. Произведение бесконечно малой функции на постоянную величину есть бесконечно малая функция.

Свойства пределов

1. Если функция имеет предел, то её можно представить как сумму постоянной, равной этому пределу, и бесконечно малой функции.

2. Если функцию можно представить как сумму постоянной величины и бесконечно малой функции, то постоянное слагаемое есть предел функции.

3. Функция у = f(x) не может иметь более одного предела при ха.

4. Предел постоянной равен этой постоянной.

5. Предел суммы (разности) двух функций равен сумме (разности) пределов этих функций:

.

6. Предел произведения двух функций равен произведению пределов этих функций:

7. Постоянный множитель можно выносить за знак предела

8. Для любых п  справедливо равенство

9. Предел частного двух функций равен частному пределов этих функций:

при условии, что

10. Если функция f(x) при х  а имеет конечный предел, то она ограничена в некоторой окрестности точки а.

11. Если для функций f(x), f₁(x) и f₂(x) в некоторой окрестности точки а выполняется неравенство

f₁(x)  f(x)  f₂(x)

и , то .

12. Если функция f(x)  0 (или f(x)  0) для всех х из некоторой окрестности точки а, кроме, быть может, самой точки а, и в точке а имеет предел, то (соответственно ).