3. Введение в математический анализ

3.1. Множества и операции над ними

Под множеством понимают семейство, совокупность, набор конечного или бесконечного числа объектов произвольной природы:

 множество всех натуральных чисел;

 множество звёзд созвездия Большой Медведицы;

 множество студентов в данной аудитории.

Объекты, из которых состоят множества, называют их элементами и обозначают малыми латинскими буквами. Сами множества обозначают большими латинскими буквами.

К основным операциям над множествами относятся: объединение множеств, пересечение множеств, разность множеств.

Объединением множеств А и В называется множество, состоящее из тех, и только тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 3.1)

Пересечением множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат и множеству А, и множеству В (рис. 3.2):

.

Разностью множеств В и А называется множество всех элементов множества В, которые не принадлежат множеству А (рис. 3.3):

.

3.2. Функция. Основные понятия

Пусть даны два множества Х и Y.

Если каждому элементу х из множества Х по определённому правилу или закону f ставится в соответствие один элемент у из множества Y, то говорят, что на множестве Х задана функция f и пишут

, или у = f(x).

При этом величина х называется аргументом функции f. Множество Х называется областью определения функции f и обозначается через D(f). Множество Y называется областью значений функции f и обозначается через E(f). Величина х называется также независимой переменной, а величина у – зависимой переменной.

Областью определения функции может быть любое множество точек числовой оси, но чаще всего в математическом анализе рассматривают лишь функции, областями определения которых служат области таких двух типов:

1. множество целых неотрицательных точек числовой оси, т.е. точек (или некоторая часть того множества);

2. один или несколько интервалов (конечных или бесконечных) числовой оси.

Говорят, что в первом случае мы имеем функцию целочисленного аргумента, а во втором — функцию непрерывного аргумента.

Например, для функции областью определения является отрезок [2, 2], областью её значений – отрезок [0, 2]. Функция определена для всех х из интервалов (, 2)  (2, ); областью её значений будут интервалы (, 0)  (0, ).

Задать функцию – значит указать область её определения и правило, по которому по данному значению независимой переменной можно найти соответствующее ему значение функции.

Важнейшими способами задания функции являются:

 табличный,

 аналитический,

 графический.

Табличный способ заключается в том, что зависимость между переменными задают с помощью таблицы: записывают ряд значений независимой переменной и соответствующие им значения функции. Хорошо известны, например, таблицы логарифмов, тригонометрических функций. Преимуществом табличного задания функции является то, что для каждого значения независимой переменной можно сразу, без вычислений, найти соответствующее значение функции.

Аналитический способ заключается в том, что зависимость между переменными величинами задаётся формулой, с помощью которой по заданным значениям независимой переменной можно получать соответствующие им значения функции.

При этом функция может быть задана как одной формулой, например , так и несколькими формулами, например

Графический способ состоит в том, что соответствие между переменными х и у задаётся с помощью графика функции. Графиком функции y = f(x) называется множество всех точек (х, у) плоскости XOY, координаты которых связаны соотношением y = f(x).

Пусть функция z = g(x) определена на множестве Х, а функция y = f(z) определена на множестве Z, причём область значений функции g содержится в области определения функции f. Функция y = f(g(x)) называется сложной функцией. Переменная х называется независимой переменной функции у, а функция z = g(x) –промежуточным аргументом функции y = f(x).

К основным элементарным функциям относятся:

 степенная функция у = х^п, n  R;

 показательная функция у = а^х, а > 0, a  1;

 логарифмическая функция y = log_ax, а > 0, a  1;

 тригонометрические функции y = sinx, y = cosx, y = tgx, y = ctgx, y = secx, y = cosecx;

 обратные тригонометрические функции y = arcsinx, y = arccosx, y = arctgx, y = arcctgx.

Элементарными функциями называются функции, полученные из основных элементарных функций и констант с помощью четырёх арифметических действий и операций формирования функции от функции, применённых конечное число раз, например, элементарными функциями являются ,

Примером неэлементарной функции является модуль действительного числа

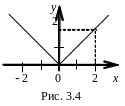
График этой функции  две полупрямые (рис. 3.4).

Функция у = f(x) называется чётной, если f(x) = f(x) для всех х из области определения функции. График чётной функции расположен симметрично относительно оси Оу. Например, функция является чётной(рис. 3.4). Функция у = cosx является чётной, поскольку выполняется равенство cos(x) = cosx (рис. 3.5).

Ф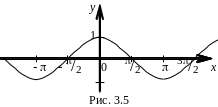 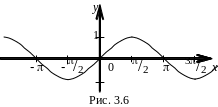ункция у = f(x) называется нечётной, если f(x) = f(x) для всех х из области определения функции. График нечётной функции расположен симметрично относительно начала координат. Например, функция у = sinx – нечётная, т. к. справедливо равенство sin(x) = sinx (рис. 3.6).

Функция у = f(x) называется периодической, если существует число Т, отличное от нуля, такое, что выполняется равенство f(x  Т) = f(x) для всех х из области определения функции. При этом наименьшее из положительных Т является периодом функции f(x).

Например, функция у = sinx имеет период Т = 2, т. е. у(х + 2n) = y(x), где n = 0, 1, 2, … (рис. 3.6).