1.5. Квадратичные формы

Однородный многочлен второй степени относительно переменных х₁ и х₂

Ф(х₁, х₂) = а₁₁ ,

не содержащий свободного члена и неизвестных в первой степени, называется квадратичной формой переменных х₁ и х₂.

Однородный многочлен второй степени относительно переменных х₁, х₂ и х₃

не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х₁, х₂ и х₃.

Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу А= . Определитель этой матрицы называется определителем квадратичной формы.

Пусть на плоскости задан ортогональный базис . Каждая точка плоскости имеет в этом базисе координаты х₁, х₂.

Если задана квадратичная форма Ф(х₁, х₂)=а₁₁ , то её можно рассматривать как функцию от переменных х₁ и х₂.

Приведение квадратичных форм к каноническому виду

Рассмотрим некоторое линейное преобразование А с матрицей .

Это симметрическое преобразование можно записать в виде:

y₁ = a₁₁x₁ + a₁₂x₂,

y₂ = a₁₂x₁ + a₂₂x₂,

где у₁ и у₂ – координаты вектора в базисе .

Очевидно, что квадратичная форма может быть записана в виде

Ф(х₁, х₂) = х₁у₁ + х₂у₂.

Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х₁ и х₂ – скалярное произведение .

Если взять другой ортонормированный базис на плоскости, то в нём квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

.

При переходе к новому базису от переменных х₁ и х₂ мы переходим к переменным и . Тогда

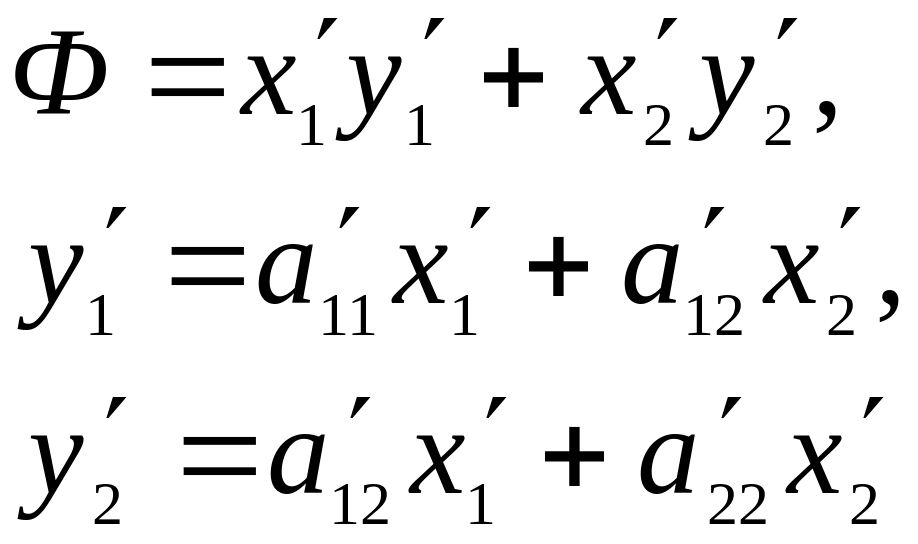
или

.

Выражение называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

Пример. Привести к каноническому виду квадратичную форму

Ф(х₁, х₂)=27 .

Решение.

Коэффициенты: а₁₁ = 27, а₁₂ = 5, а₂₂ = 3.

Составим характеристическое уравнение: ;

(27 - )(3 - ) – 25 = 0,

² - 30 + 56 = 0 ₁ = 2; ₂ = 28;

1.6. Исследование систем линейных уравнений. Теорема Кронекера-Капелли

Система m уравнений с n неизвестными в общем виде записывается следующим образом:

,

где a_ij – коэффициенты, а b_i – постоянные.

Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.

Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

Для системы линейных уравнений матрица

А=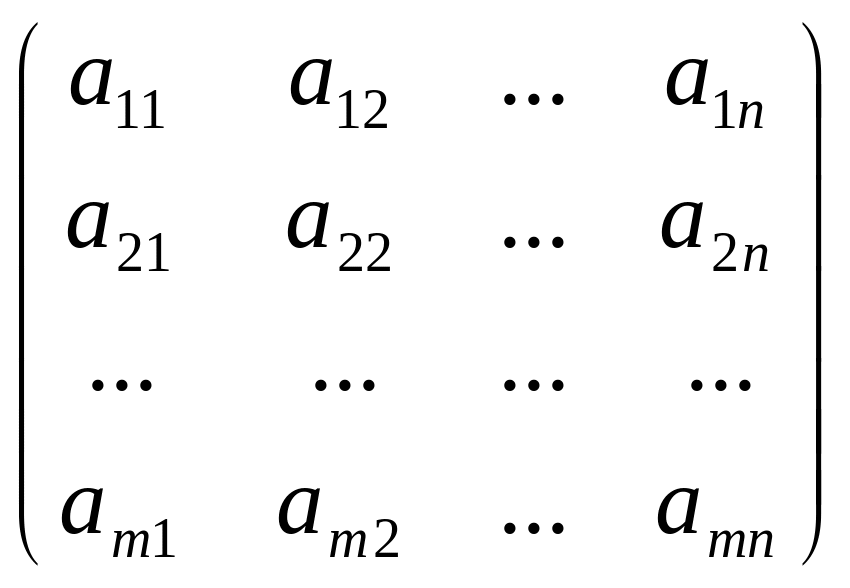 называется матрицей системы, а матрица

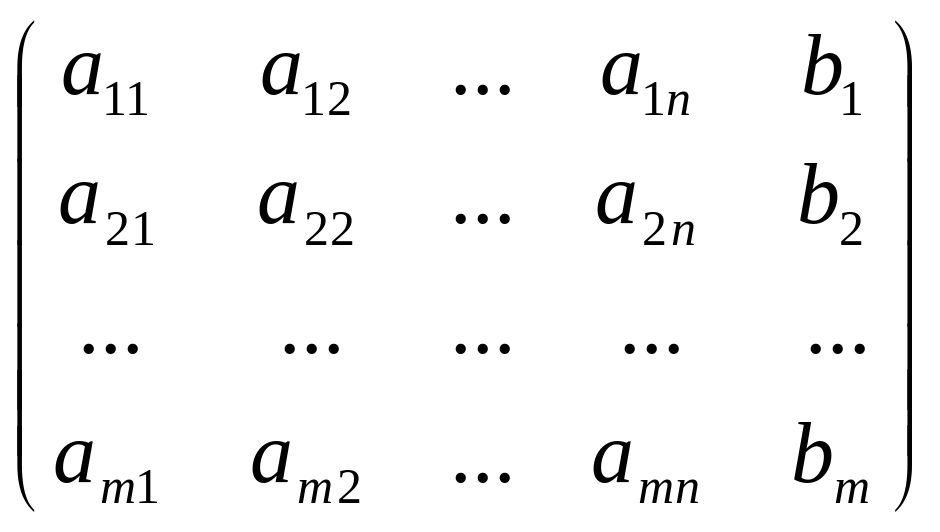= называется расширенной матрицей системы.

К элементарным преобразованиям относятся:

1) прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.

2) перестановка уравнений местами.

3) удаление из системы уравнений, являющихся тождествами для всех х.

Теорема Кронекера – Капелли (условие совместности системы)

Для того чтобы система линейных уравнений была совместна необходимо и достаточно чтобы ранг её матрицы был равен рангу расширенной матрицы системы .

Если ранг матрицы А равен рангу расширенной матрицы и равен n числу неизвестных, то система имеет единственное решение.

Если ранг матрицы А равен рангу расширенной матрицы, но меньше n числа неизвестных, то система имеет бесконечное число решений.

Если ранг матрицы А меньше ранга расширенной матрицы и равен n числу неизвестных, то система не имеет решения.

.

Решаем данную систему так:

Выделим любые r уравнений и r неизвестных, но так чтобы определитель был отличен от нуля.

- основные (базисные) переменные;

- свободные переменные.

Перенесем слагаемые со свободными неизвестными в правую часть.

Решим полученную систему относительно основных переменных, предавая свободным переменным произвольные значения, получим для основных переменных бесконечное множество решений.

Пример. Определить совместность системы линейных уравнений:

_{Решение.}

~ .

,

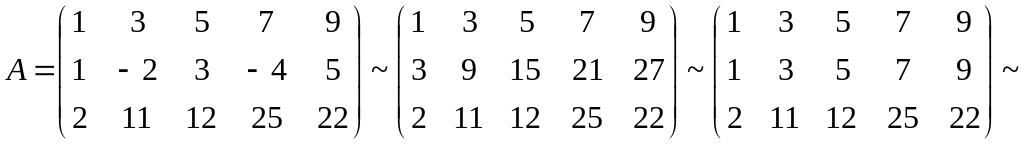
RgA=2.

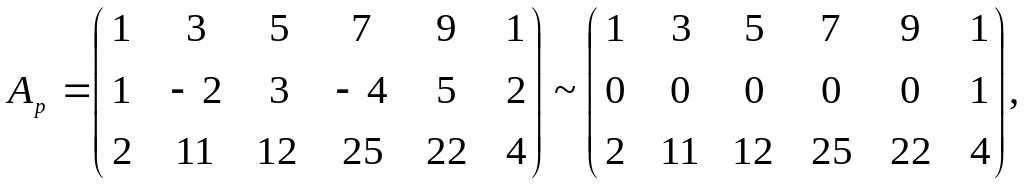
Rg =3.

Система несовместна.

П ример. Исследовать систему уравнений.

2х₁+7х₂+3х₃+х₄=6;

3х₁+5х₂+2х₃+2х₄=4;

9х₁+4х₂+х₃+7х₄=2.

_{Решение.}

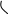
- система имеет бесчисленное множество решений.

х₁; х₂- основные переменные, (первые два уравнения);

х₃; х₄- свободные переменные.