Курс лекций

1. Линейная алгебра

1.1. Матрицы. Основные понятия. Операции над матрицами

Матрицей размером mn называется множество каких-либо элементов, расположенных в виде прямоугольной таблицы, состоящей из m-строк n-столбцов.

Матрица обозначается заглавными буквами латинского алфавита A,B,C,….

.

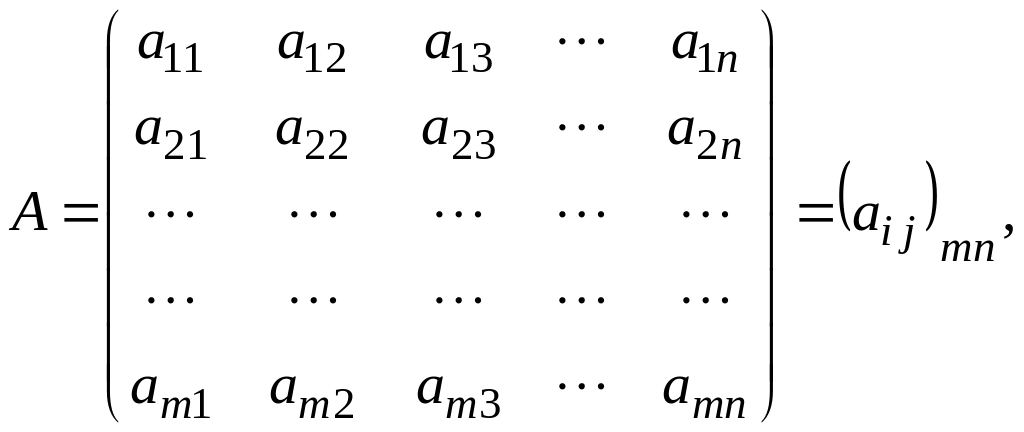
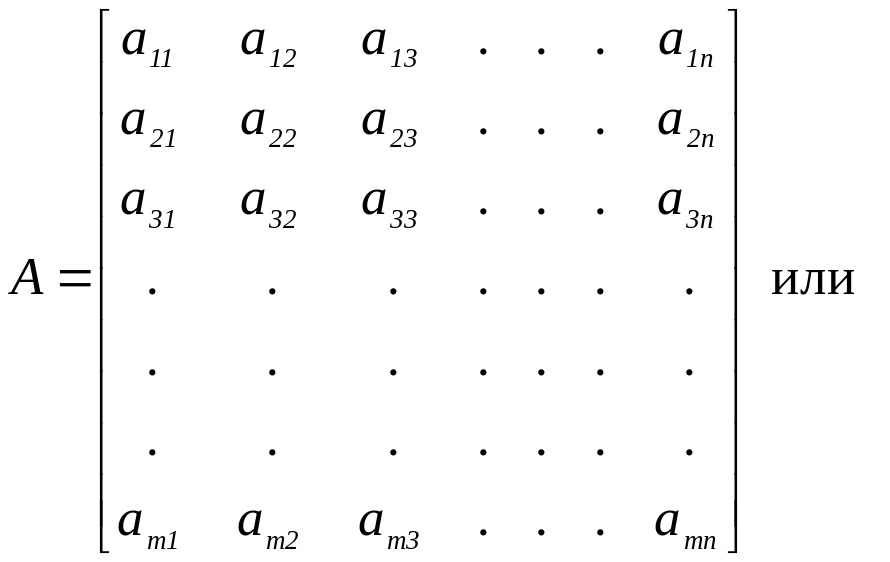
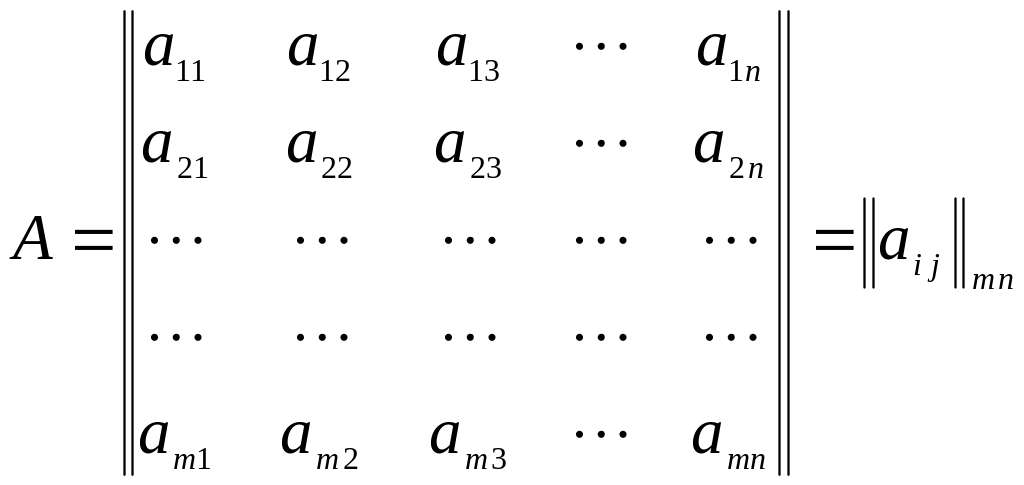Здесь a_ij - элементы матрицы. Каждый элемент имеет два индекса, первый i обозначает номер строки (i = 1, 2, …, m), а второй j — номер столбца. (j = 1, 2, …, n). Элементами матрицы могут быть числа, функции, векторы и т. д.

Рассмотрим некоторые виды матриц.

Если m=n, то матрица квадратная порядка n

.

Матрица, состоящая из одной строки, называется строчной

.

Матрица, состоящая из одного столбца, называется столбцовой

.

Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной

.

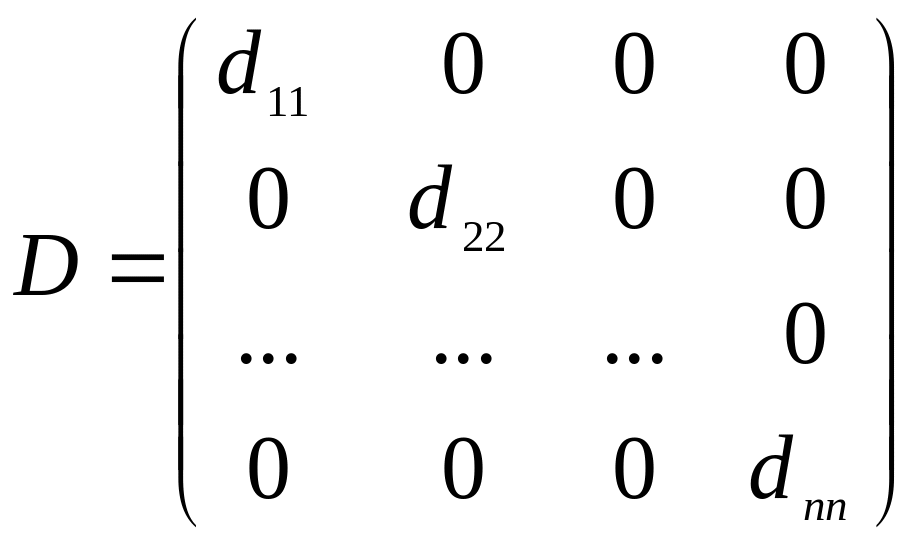Диагональная матрица, у которой все элементы равны единице, называется единичной .

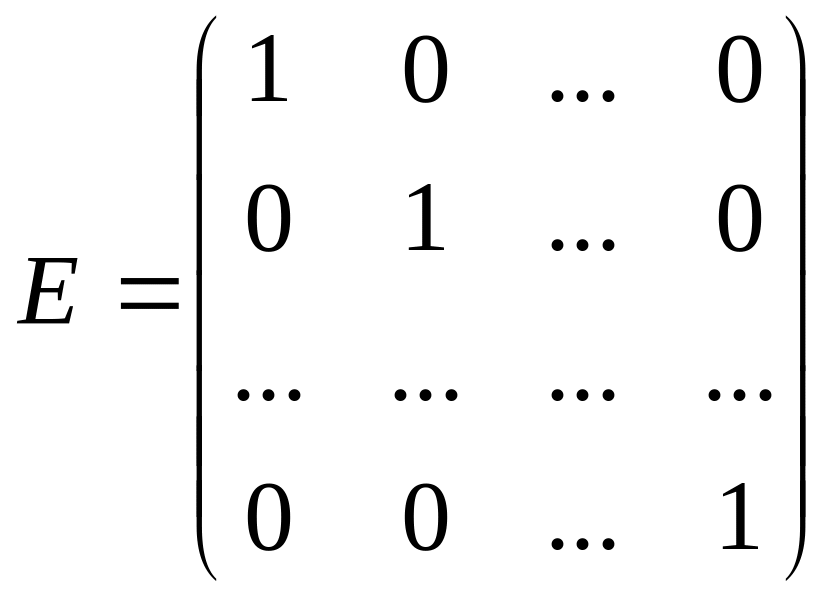Если в матрице А поменять местами строчки и столбцы то полученная матрица называется транспонированной.

, то .

Две матрицы А и В равны между собой, если они одинакового размера и их соответствующие элементы равны, т.е.

А=В, если a_ij=b_ij ( i=1,2,…m; j=1,2,…,n).

Сложение матриц

Складывать можно только матрицы одинакового размера по правилу

, , ,

.

Пример. Найти матрицу , если , .

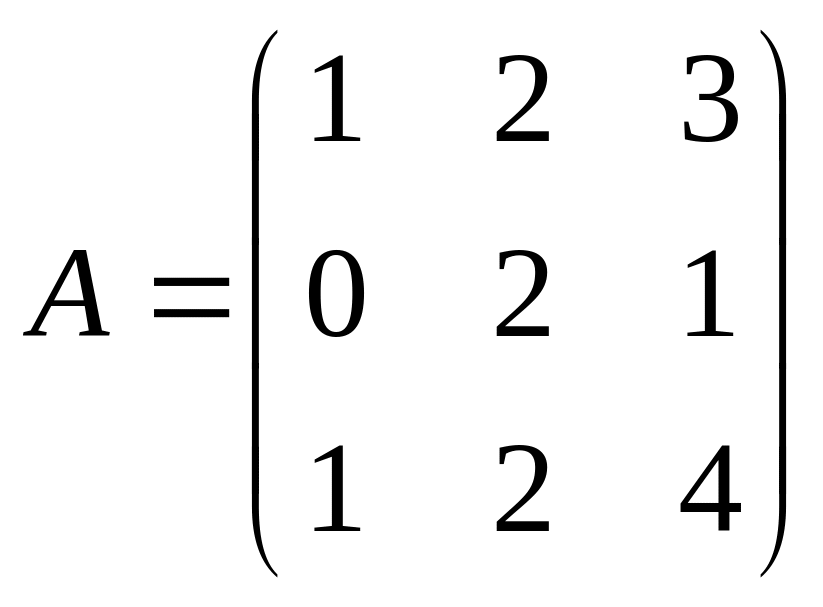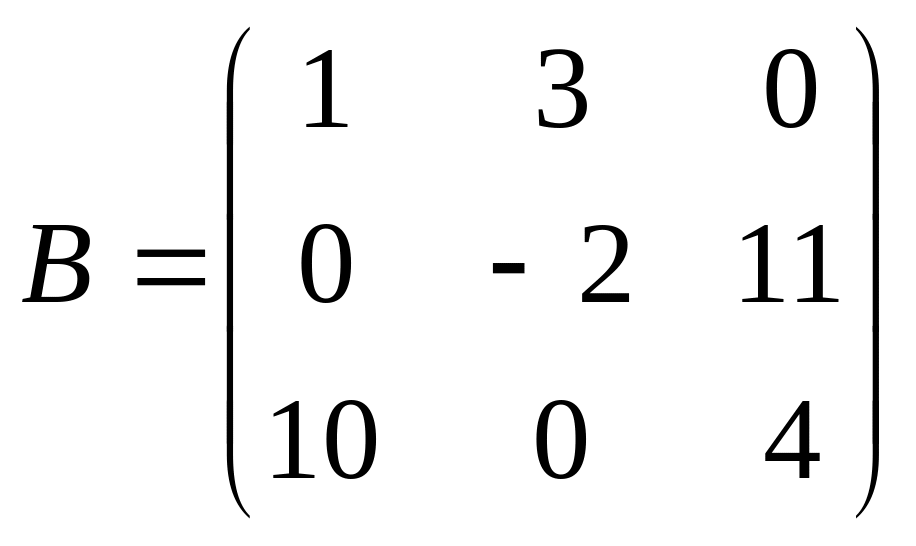Решение.

.

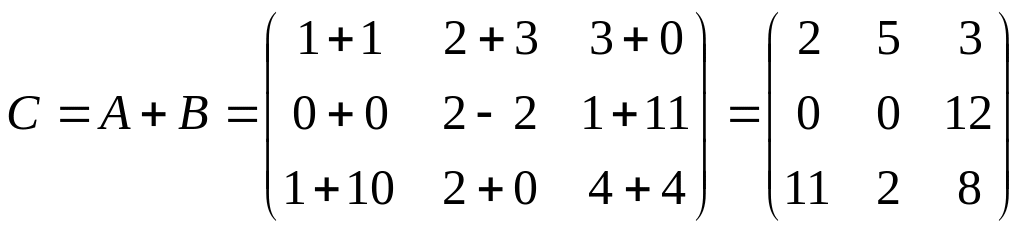Свойства сложения матриц

A+B=B+A;

A+(B+C)=(A+B)+C=A+B+C.

Умножение матрицы на число

Чтобы умножить матрицу на число  надо умножить на это число каждый элемент матрицы. , B=A , .

Свойства умножения матрицы на число

, ,

(+)A=A+A,

()A=(B).

Пример. Найти матрицу если

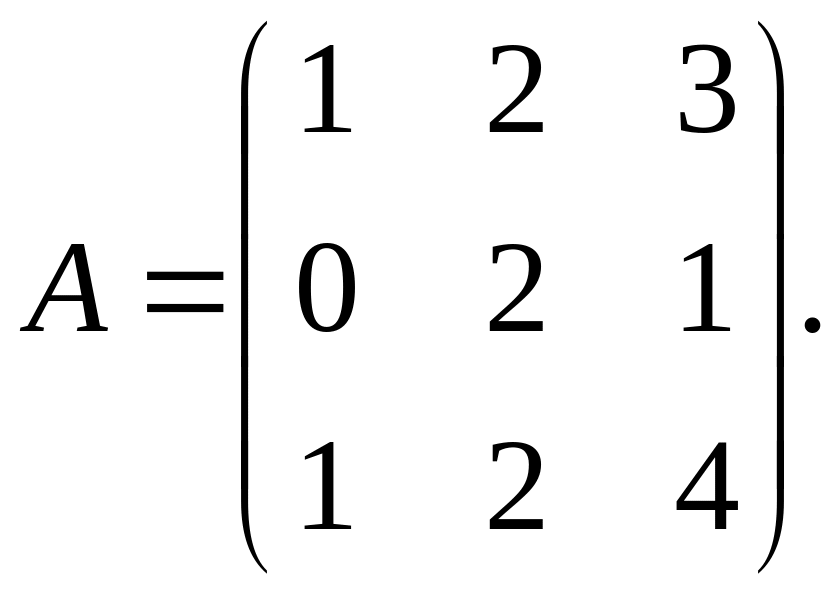
Решение.

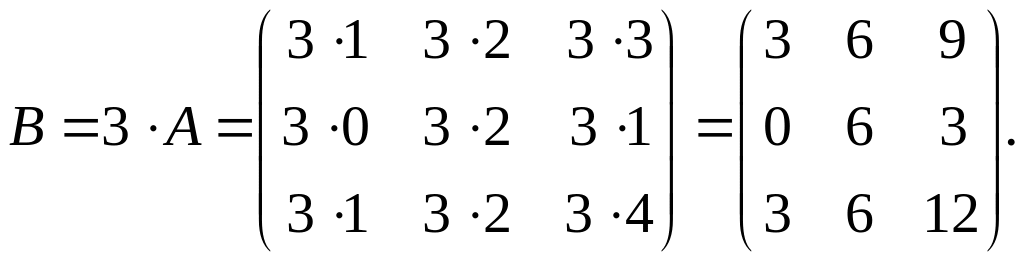
Пример. Найти матрицу , если .

Решение.

.

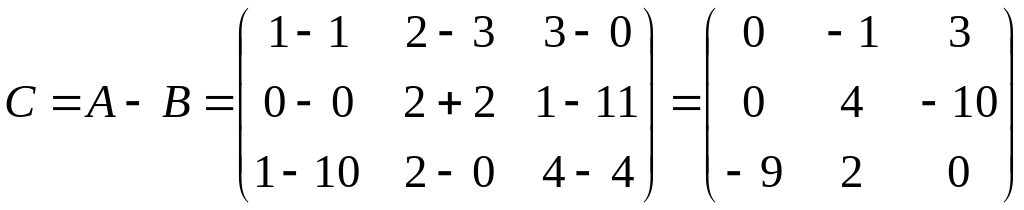Произведение двух матриц

Умножать можно только те матрицы, для которых число столбцов в первой матрицы равно числу строк во второй матрицы. Произведением двух матриц 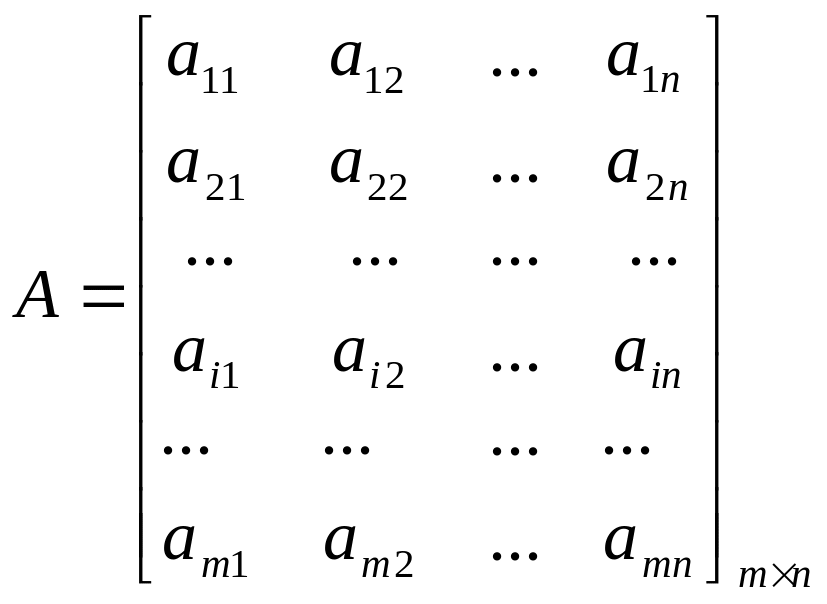, 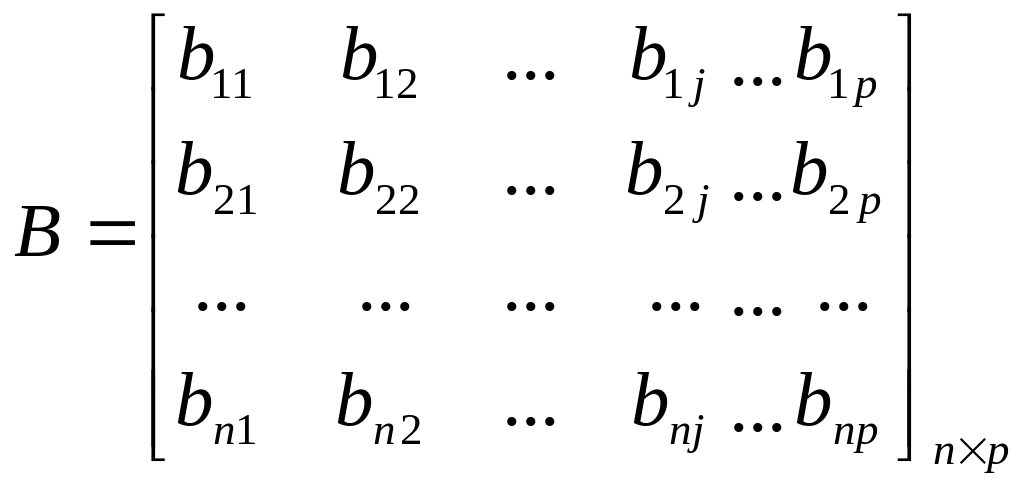называется матрица 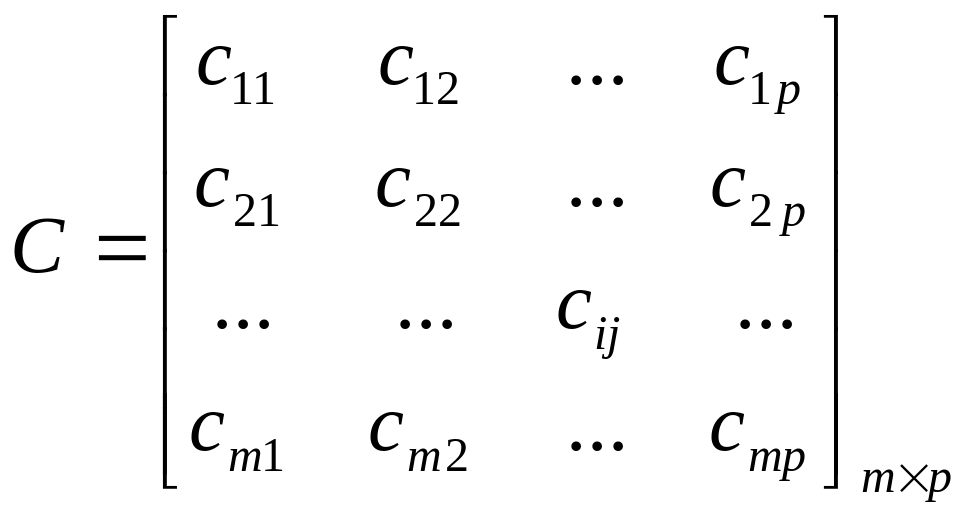, у которой элемент c_ij находится по формуле

, i=1,2,…,m; j=1,2,…,p,

т.е. элемент матрицы c_ij , стоящий на пересечении i – строки и j-столбца, равен сумме произведений элементов i – строки матрицы А на соответствующие элементы j-столбца матрицы В. В результате умножения матрицы А на матрицу В получится матрица С, число строк которой равно числу строк матрицы А, а число столбцов равно числу столбцов матрицы В.

Пример. Перемножить матрицы А и В, если , .

Решение.

.

Если АВ=ВА, то матрицы коммутативные.

1.2. Определители и их свойства

Определителем квадратной матрицы или просто определителем (детерминантом) называется число, которое ставится в соответствие матрице и может быть вычислено по её элементам.

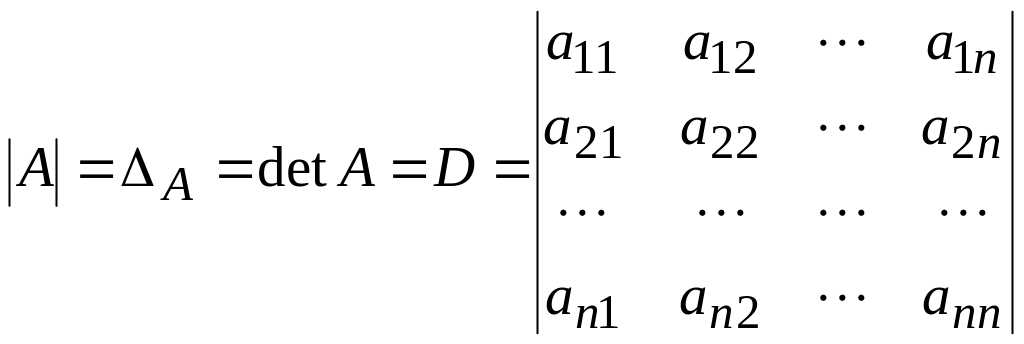
Квадратная матрица первого порядка состоит из одного элемента, поэтому её определитель равен самому элементу .

Определитель второго порядка вычисляется по формуле: .

Определитель третьего порядка вычисляется по правилу треугольника: .

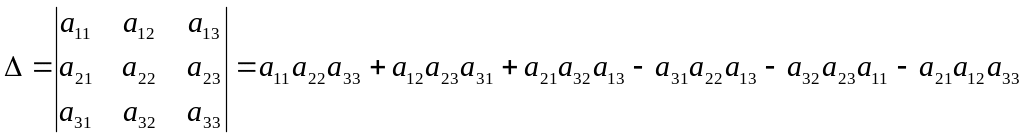Минором M_ij элемента a_ij определителя п-го порядка называется определитель (п  1)-го порядка, полученный из данного определителя путём вычёркивания элементов i-той строки и j-того столбца.

Алгебраическим дополнением A_ij элемента a_ij определителя  называется число A_ij = (1)^i + jM_ij.

Таким образом, алгебраическое дополнение A_ij элемента a_ij – это соответствующий минор M_ij, умноженный на .

Вычисление определителей

Теорема (без доказательств) о разложении определителя по элементам строки (столбца).Для каждой квадратной матрицы А порядка n имеет место формула

, если ;

, если .

Пример. ,

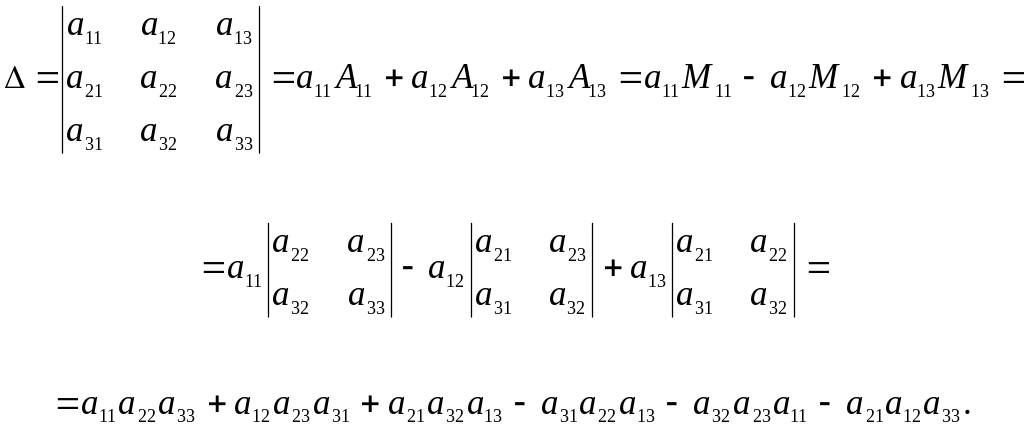
Свойства определителей

1. При транспонировании величина определителя не меняется.

Строки и столбцы определителя эквиваленты.

2. Если в определители поменять местами какие-либо две строки (столбца) местами, то определитель меняет знак.

3. Определитель с двумя одинаковыми столбцами (строками) равен нулю.

4. При умножении элементов какого-либо столбца (строки) на число , определитель умножается на это число.

.

5. Если все элементы какого-либо столбца (строки) равны нулю, то определитель равен нулю.

6. Если элементы двух строк (столбцов) пропорциональны, то определитель равен нулю.

7. Пусть каждый элемент какого-либо столбца (строки) определителя равен сумме двух слагаемых, тогда этот определитель равен сумме двух определителей, причём в первом их них соответствующий столбец (строка) состоит из первых слагаемых, а во втором - из вторых слагаемых.

8. Определитель не изменится, если к элементам какого-либо столбца (строки) прибавить соответствующие элементы другого столбца, умноженного на одно и тоже число.

где

9. Сумма произведений элементов какого-либо столбца определителя на алгебраического дополнения к элементам другого столбца равна нулю.

Пример. Вычислить определитель

_{Решение.}

1. По правилу треугольника:

2. Разложение по первой строке:

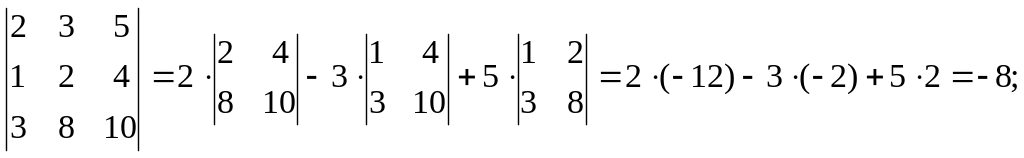
3. Преобразование первого столбца: