Декодування циклічних кодів з використанням схем ділення першого і другого типу

11.1 Мета роботи

Вивчення принципiв синтезу i дослiдження роботи декодуючих пристроїв повних циклiчних кодiв з застосуванням схем дiлення першого та другого типу.

11.2 Варіанти завдань

11.2.1 Дослiдження i синтез декодера повного циклiчного (7,4) кода, утвореного багаточленом х³+х+1, із застосуванням схем дiлення першого типу.

11.2.2 Дослiдження i синтез декодера повного циклiчного (7,4) кода, утвореного багаточленом х³+х²+1, з застосуванням схем дiлення першого типу.

11.2.3 Дослiдження i синтез декодера повного циклiчного (7,3) кода, утвореного багаточленом х⁴+х³+х²+1, з застосуванням схем дiлення першого типу.

11.2.4 Дослiдження i синтез декодера повного циклiчного (7,3) коду, утвореного багаточленом х⁴+х+1, з застосуванням схеми дiлення першого типу.

11.2.5 Дослiдження i синтез декодера повного циклiчного (7,3) коду, утвореного багаточленом х⁴+х³+1, з застосуванням схеми дiлення першого типу.

11.2.6 Дослiдження i синтез декодера повного циклiчного (7,3) коду, утвореного багаточленом х⁴+х²+х+1, з застосуванням схеми дiлення першого типу.

11.2.7 Дослiдження i синтез декодера повного циклiчного (7,4) кода, утвореного багаточленом х³+х+1, із застосуванням схем дiлення другого типу.

11.2.8 Дослiдження i синтез декодера повного циклiчного (7,4) кода, утвореного багаточленом х³+х²+1, з застосуванням схем дiлення другого типу.

11.2.9 Дослiдження i синтез декодера повного циклiчного (7,3) кода, утвореного багаточленом х⁴+х³+х²+1, з застосуванням схем дiлення другого типу.

11.2.10 Дослiдження i синтез декодера повного циклiчного (7,3) коду, утвореного багаточленом х⁴+х+1, з застосуванням схеми дiлення другого типу.

11.2.11 Дослiдження i синтез декодера повного циклiчного (7,3) коду, утвореного багаточленом х⁴+х³+1, з застосуванням схеми дiлення другого типу.

11.2.12 Дослiдження i синтез декодера повного циклiчного (7,3) коду, утвореного багаточленом х⁴+х²+х+1, з застосуванням схеми дiлення другого типу.

11.3 Основні теоретичні відомості

Найбільш поширеним методом декодування циклічних кодів є метод, що грунтується на обчисленні синдрому, як залишку від ділення довільного багаточлена , що відповідає прийнятій комбінації на утворюючий багаточлен .

В загальному випадку:

(11.1),

де – багаточлен, що відповідає переданій комбінації, – багаточлен помилки. Оскільки має властивість ділиться на багаточлен без залишку, то вид синдрому (залишку) при діленні повністю визначається тільки помилками , що спотворювали прийняту комбінацію. Нульовий синдром розглядається як підтвердження відсутності помилок, тобто співпадання та .

Увипадку виправлення помилки, декодування здійснюється в два етапи (цикли). По-перше, обчислюється залишок (синдром) від ділення на , а після того по вигляду залишку виділяється місце помилки і здійснюється корекція прийнятої комбінації.

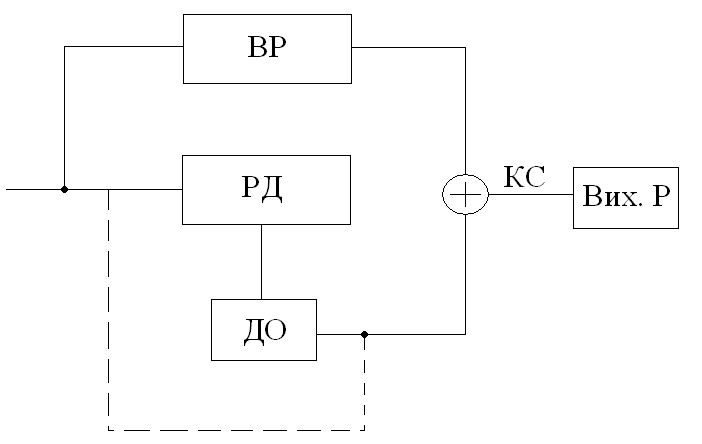
Рисунок 11.1 Узагальнена структурна схема декодуючого пристрою

Символи кодової комбінації, що можливо містять помилки, послідовного, починаючи з старшого розряду, поступають у вхідний регістр ВР і одночасно в генератор синдрому (регістр ділення) РД.

Вхідний регістр призначений для тимчасового зберігання декодованої послідовності і складається з комірок. В регістрі РД за тактів визначається залишок (перший цикл). Починаючи з такту, здійснюється зчитування елементів з ВР (цикл корекції). В кожному такті одночасно із зчитуванням з ВР відбувається зсув генератора синдрому на один крок і в ньому з’являється новий залишок. Новий залишок буде синдромом зсунутої комбінації помилок. Так, якщо код виправляє тільки поодинокі помилки і синдром після перших тактів ділення відповідає помилці в четвертому елементі (елементи нумеруються починаючи із старшого), то на такті з’являється залишок, що відповідає спотворенню третього елемента, на такті – спотворенню другого елемента і так далі. Стан комірок пам’яті контролюється схемою детектора помилок , яка є комбінаційною логічною схемою. При стані комірок РД, що відповідає помилці в першому елементі, вихід буде відмінний від 0. Отже, коли помилковий символ займе крайню праву комірку в регістрі ВР, а РД сформується залишок, що відповідає спотворенню першого елемента і на виході з’явиться сигнал “1”. У наступному такті символ, що зчитується з ВР, додається в коректоючому суматорі КС з вихідним сигналом і на виході КС з’явиться виправлений елемент. Як ланка корекції використовується суматор по модулю.

Після виявлення та виправлення помилки всі комірки РД повертаються в нульовий стан. Це досягається шляхом подачі сигналу з входу на вхід РД (пунктирна лінія). Якщо до кінця циклу корекції ( через такта) стан РД не виявиться нульовим, то це означає, що помилка не виправилася, тобто помилка вищої кратності.

На виході пристрою встановлений регістр зсуву з комірками Вих.Р, в який виводяться інформаційні елементи після проходження через комірку КС. Заповнення Вих. Р відбувається з по такти. Вміст даного регістру зберігається до наступної комбінації коду і використовується в наступних схемах обробки інформації.

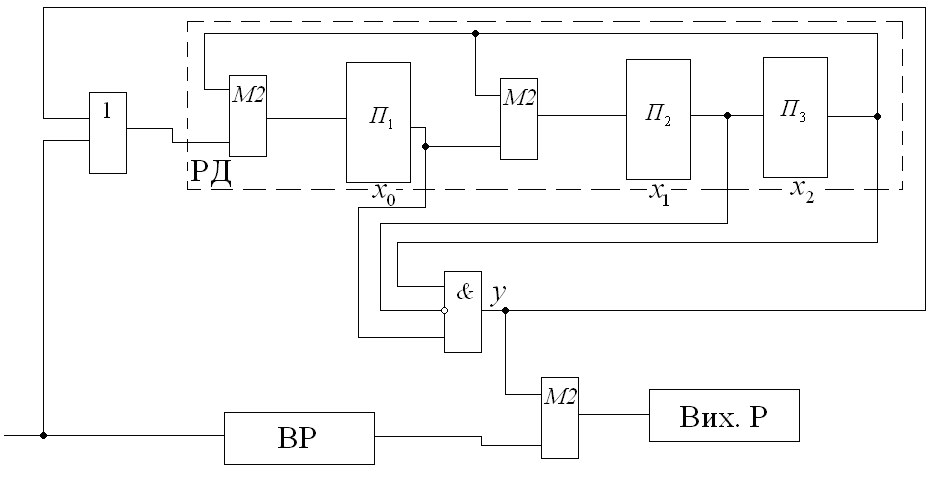
Рисунок 11.2 Схема пристрою декодування (7,4) – коду з утворюваним багаточленом

Код виправляє всі помилки першої кратності, перевірочна матриця коду має такий вигляд:

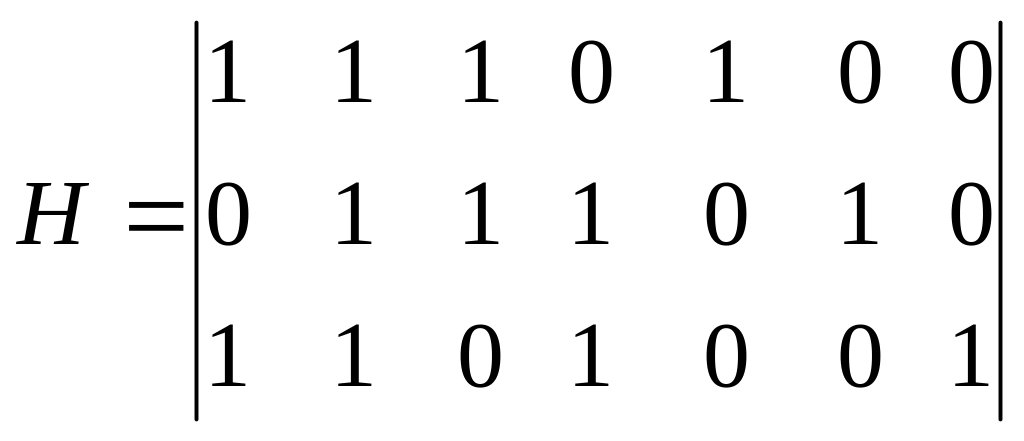(11.2)

забезпечує формування вихідного сигналу тільки при появі залишку 101, тобто реалізує логічну функцію . Регістр ділення, що використовується в пристрої можна умовно назвати схемою ділення першого типу.

У відповідності із матрицею (11.2) може бути складена таблиця декодування (таблиця 11.1)

Таблиця 11.1 Таблиця декодування при використанні схеми ділення першого типу

Вектор помилки	Багаточлен	Залишок	Вектор помилки	Багаточлен	Залишок
0000000	0	000	0001000	х3	011
1000000	х6	101	0000100	х2	100
0100000	х5	111	0000010	х1	010
0010000	х4	110	0000001	х0	001

Розглянемо декодування повних циклічних кодів з застосуванням схем ділення другого типу.

При використаннi в процесi декодування регiстру дiлення, призначеного для кодування (п. 10.4), вiдповiднiсть мiж векторами помилок i залишками на тактi буде iнша (п. 11.4).

Вказаний регiстр дiлення можна назвати схемою дiлення другого типу. В даному випадку замiсть обчислення синдрому полiнома визначається синдром полiному (по модулю ), що рiвносильно, як вказувалось ранiше, знаходженню залишку вiд дiлення на . Так, якщо помилка з'явилась в старшому розрядi , то залишок вiд дiлення на дорiвнює (в двiйковому представленнi – 100)

Таблиця 11.2 є таблицею декодування розглянутого вище коду з застосуванням дiлення другого типу.

Таблиця 11.2 – Таблиця декодування при використаннi схеми дiлення другого типу

Вектор помилки	Багаточлен	Залишок	Вектор помилки	Багаточлен	Залишок
0000000	0	000	0001000	х3	101
1000000	х6	100	0000100	х2	111
0100000	х5	010	0000010	х1	110
0010000	х4	001	0000001	х0	011

При декодуваннi коду з всi поодинокi помилки виправляються, а помилки другої кратностi виявляються. Функцiонування пристрою в цьому випадку вiдрiзняється вiд розглянутого вище тим, що при появi в кiнцi циклу корекцiї залишку, вiдмiнного вiд 0, iнформацiя, записана у вихiдному регiстрi, знищується. В схемi модуля стирання iнформацiї при виявленнi помилок, що не виправляються, здiйснюється на другому тактi. Якщо залишок нульовий, то вмiст зберiгається.

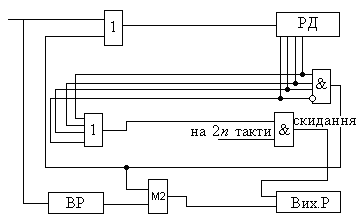
Рисунок 11.3

Схема вiдповiдного пристрою наведена на рисунку 11.3. Вона складена для (7,3)-коду з утворюючим багаточленом.

11.4 Порядок виконання робіт циклу

11.4.1 Ознайомитися з описом лабораторної роботи і короткими відомостями з теорії.

11.4.2 Отримати у викладача технічне завдання.

11.4.3 Скласти структурну схему декодування.

11.4.4 Використовуючи засоби автоматизованого проектування MAX+II: створити графічний проект, скомпілювати та провести функціональне моделювання логічної функції.

11.4.5 Отримати дані експерименту.

11.5 Контрольні питання

11.5.1 Записати число 1011100 у виглядi багаточлена.

11.5.2 Залишок вiд дiлення 10000000 на багаточлен 11001.

11.5.3 Синдром, що вiдповiдає помилцi в старшому розрядi (7,4)- коду при g(x)=х³+х²+1.

11.5.4 Синдром, що видiляється схемою детектора помилки при використаннi схем дiлення першого та другого типiв.

11.5.5 Перевiрочна матриця для (5,2)-коду.

11.5.6 Кiлькiсть варiантiв помилок, що виправляється циклiчним (7,4)-кодом.

11.5.7 Схеми дiлення другого типу.

11.5.8 Складання таблиць декодування при застосуваннi схем дiлення другого типу.

11.5.9 Коректуючi можливостi декодуючих пристроiв, що реалiзують схеми дiлення другого типу.

11.5.10 Процес декодування довiльної комбiнацiї при вiдсутностi i наявностнi помилок.

Список рекомендованої літератури

1. С.І. Мельничук. Основи автоматизованого проектування елементів та засобів обчислювальної техніки: Навчально-методичний посібник. – Івано-Франківськ: видавництво ІМЕ, 2004. - 180 с.

2. Ю.П. Жураковський, В.П. Полторак. Теорія інформації та кодування: Підручник – К.: Вища школа, 2001. - 255 с.

3. Игнатов В.А. Теория информации и передачи сигналов. – Радио и связь, 1991. – 280 с.

4. А.Г. Зюко и др. Помехоустойчивость и эффективность

систем передачи информации. – М.: Радио и связь, 1985. – 272 с.

5. Тутевич В.М. Телемеханика. Учебн. пособие для студ.

вузов. 2-е изд., перероб. и доп. – М.: Выcш. школа, 1985. – 423 с.

6. Лабораторний практикум з курсу “ Телемеханіка та

передача інформації в нафтовій і газовій промисловості ” Ч. 1., Ч. 2., ІФНТУНГ, ФАКЕЛ, 1999 р.

99