Кодування циклічних кодів методами ділення інформаційних символів на утворюючий багаточлен та визначення провірочних символів під час проведення лінійни операцій

10.1 Мета роботи

Вивчення принципiв синтезу (n,k)-кодiв методом обчисленя перевiрочних символiв в результатi проведення лiнiйних операцiй та методом дiлення iнформацiйних символiв на утворюючий багаточлен i дослiдження роботи кодерiв, що застосовуються в системах телемеханiки.

10.2 Варіанти завдань

10.2.1 Дослiдження i синтез кодера повного циклiчного (7,4)- коду з утворюючим багаточленом х³+х+1 методом обчислення перевiрочних символiв.

10.2.2 Дослiдження i синтез кодера повного циклiчного (7,4)- коду з утворюючим багаточленом х³+х²+1 методом обчислення перевiрочних символiв.

10.2.3 Дослiдження i синтез кодера повного циклiчного (7,3)- коду з утворюючим багаточленом х⁴+х³+х²+1 методом обчислення перевiрочних символiв.

10.2.4 Дослiдження i синтез кодера повного циклiчного (7,3)- коду з утворюючим багаточленом х⁴+х²+х+1 методом обчислення перевiрочних символiв.

10.2.5 Дослiдження i синтез кодера повного циклiчного (7,3)- коду з утворюючим багаточленом х⁴+х+1 методом обчислення перевiрочних символiв.

10.2.6 Дослiдження i синтез кодера повного циклiчного (7,3)- коду з утворюючим багаточленом х⁴+х³+1 методом обчислення перевiрочних символiв

10.2.7 Дослiдження i синтез кодера повного циклiчного (7,4) коду методом дiлення iнформацiйних символiв на утворюючий багаточлен x³+x+1.

10.2.8 Дослiдження i синтез кодера повного циклiчного (7,4) коду методом дiлення iнформацiйних символiв на утворюючий багаточлен x³+x²+1.

10.2.9 Дослiдження i синтез кодера повного циклiчного (7,3) коду методом дiлення iнформацiйних символiв на утворюючий багаточлен x⁴+x³+x²+х+1.

10.2.10 Дослiдження i синтез кодера повного циклiчного (7,3) коду методом дiлення iнформацiйних символiв на утворюючий багаточлен x⁴+x³+x²+1.

10.2.11 Дослiдження i синтез кодера повного циклiчного (7,3) коду методом дiлення iнформацiйних символiв на утворюючий багаточлен x⁴+x²+х+1.

10.2.12 Дослiдження i синтез кодера повного циклiчного (7,3) коду методом дiлення iнформацiйних символiв на утворюючий багаточлен x⁴+x+1.

10.3 Основні теоретичні відомості

Циклічним кодом називається лінійний систематичний код, який разом із своїм кодовим словом містить і його циклічний зсув. Існує два методи кодування циклічних кодів методом обчисленя перевiрочних символiв в результатi проведення лiнiйних операцiй та методом дiлення iнформацiйних символiв на утворюючий багаточлен.

Розглянемо перший метод. Основними приладами, що використовуються при кодуваннi i декодуваннi циклiчних кодiв, є регiстри зсуву з логiчними зв'язками (лiнiйнi перимикальнi схеми), що здiйснюють як множення так i дiлення багаточленiв.

При кодуваннi з джерела поступають блоки з iнформацiйних символiв ( ), якi передаються в канал зв'язку i доповнюються перевiрочними символами ( ). Таким чином, кожному блоку з iнформацiйних символiв в пристрої кодування спiвставляється розрядний кодовий вектор:

(10.1)

Алгоритм кодування циклiчних кодiв методом дiлення iнформацiйних символiв на утворюючий багаточлен передбачає обчислення символiв перевiрки, як одержання залишку вiд дiлення багаточлена на утворюючий багаточлен , де багаточлен, що вiдповiдає довiльнiй iнформацiйнiй послiдовностi на входi пристрою кодування. Дозволена кодова комбiнацiя циклiчного коду одержується шляхом додавання залишку до кодової комбiнацiї простого коду , тобто:

(10.2)

Cукупнiсть кодових комбiнацiй циклiчного (n,k)-коду може бути представлена утворюваною матрицею . , де – одинична матриця розмiрностi (к,к), -матриця залишкiв, розмiрнiсть якої (k,r).

Для обчислення залишкiв використовують схеми дiлення на фiксований багаточлен. У кодуючому пристрої найбiльш доцiльно використовувати схеми, якi поєднують в собi операцiї множення на одночлен i дiлення на , що дозволяє обчислити значення символiв перевiрки (залишок) за тактiв.

Рисунок 10.1 Пристрій кодування, що використовує схему ділення на утворюючий багаточлен

Пристрій кодування, що використовує подібну схему для ділення, представлено на рисунку 10.1. В ній утворюючий багаточлен . Схема дiлення складається з комірок пам'ятi ( ) i двох суматорiв по модулю два. На вхiд пристрою подається довiльна послiдовнiсть розрядного надлишкового коду, починаючи з коефiцiєнтiв старших розрядiв.

У вихiдному станi всi чарунки пам'ятi знаходяться в станi "0", коньюнктори 1 i 3 вiдкритi, а елемент 2 закритий. Iнформацiйнi символи одночасно поступають як в канал зв'язку (з входу) так i в регiстр дiлення, де за чотири такта формується залишок, тобто розряди перевiрки . Потiм коньюнктори 1 i 3 закриваються, а елемент 2 вiдкривається i за наступнi три такта елементи перевiрки виводяться в канал зв'яку. Переключення елементiв 1, 2, 3 здiйснюється вiд блоку управлiння.

Слiд пам'ятати, що неприведений багаточлен утворює повний циклiчний (7,4)-код, матриця якого:

(10.3)

Розглянемо другий метод. Оскiльки циклiчний код вiдноситься до лiнiйного коду, то значення його перевiрочних розрядiв можуть бути визначенi в результатi проведення лiнiйних операцiй над вiдомими iнформацiйними розрядами. Але в силу властивостей циклiчного коду достатньо визначити лiнiйну операцiю тiльки для одного перевiрочного елементу. Ця операцiя повнiстю задається перевiрочним полiномом.

, де багаточлен, cпряжений з утворюючим багатогочленом .

Визначивши i провiвши циклiчний зсув, одержуємо кодове слово, яке також вiдноситься до циклiчного коду. За елементами цiєї комбiнацiї тепер обчислюють наступний перевiрочний елемент, знову проводять циклiчний зсув i т.д. Отже, для формування кодових комбiнацiй циклiчного коду необхiдно мати пристрiй, який у вiдповiдностi з багаточленом обчислює i за вiдомими значеннями iнформацiйних елементiв.

Нехай циклiчний (7,4)-код заданий багаточленом . Тодi спряжений багаточлен , перевiрочний полiном

, а лiнiйне рiвняння, що йому вiдповiдає є .

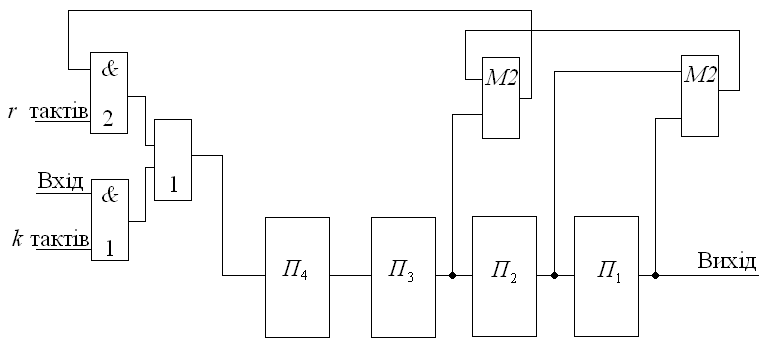Рис. 10.2 Схема кодуючого присторою за допомогою методу обчислення перевірочних символів в результаті проведення лінійних операцій

Кодуючий пристрiй (рисунок 10.2) будується на основi розрядного регiстру зсуву. Вихiд комірок пам'ятi пiд'єднується до суматорiв по модулю два у вiдповiдностi з вище навединим лiнiйним рiвнянням. У початковому станi коньюнктор 1 вiдкритий, а елемент 2 знаходиться в закритому станi. За першi тактiв, iнформацiйнi символи, що поступають на вхiд, заповнюють комірки регiстру. Причому старший розряд досягає комірки . Потiм елемент 1 вiдключається, а елемент 2 вiдкривається. На кожному з наступних тактiв один iнформацiйний символ подається на вхiд схеми (в канал зв'язку) i одночасно по ланцi зворотнього зв'язку формується один перевiрочний розряд. Через тактiв процес формування перевiрочних розрядiв закiнчиться. До цього моменту часу в комірцi мiститься елемент , а в комірках вiдповiдно перевiрочнi елементи . Протягом наступних тактiв вмiст регiстру подається в канал зв'язку. Перемикання коньюнкторiв 1 та 2 здiйснюється сигналами з блоку управлiння.

10.4 Порядок виконання робіт циклу

10.4.1 Ознайомитися з описом лабораторної роботи і короткими відомостями з теорії.

10.4.2 Отримати у викладача технічне завдання.

10.4.3 Намалювати принципову схему кодера циклiчного коду.

10.4.4 Використовуючи засоби автоматизованого проектування MAX+II: створити графічний проект, скомпілювати та провести функціональне моделювання логічної функції.

10.4.5 Отримати дані експерименту.

10.5 Контрольнi питання

10.5.1 Перевiрочний полiном .

10.5.2 Багаточлен, спряжений з утворюючим багаточле-ном.

10.5.3 Лiнiйнi рiвняння для знаходження перевiрочних елеменетiв.

10.5.4 Паралельний ввiд iнформацiї в комірки регiстру.

10.5.5 Розмiрнiсть утворювачої матрицi циклiчного коду.

10.5.6 Вибiр числа перевiрочних розрядiв для коду з .

10.5.7 Фактори, що визначають степiнь утворюваного багаточлену.

10.5.8 Вибiр утворюючого багаточлену для коду, що виправляє поодинокi помилки.

10.5.9 Вид комбiнацiї циклiчного коду при інформацій-ній частинi 1001 i .

Лабораторна робота №11