
- •Створення і дослідження мультиплексорів, претворення паралельного коду в послідовний
- •Створення і дослідження шифраторів (позиційного кодув двійковий, двійковий в десятковий) на основі логічних елементів
- •Створення і дослідження дешифраторів (двійкового коду, двійководесяткового в позиційний) на основі логічних елементів
- •Визначення кількості інформації, оцінка інформаційних втрат та швидкості передачі для дискретних інформаційних каналів
- •Побудова кодів, які виявляють помилки для заданого ансамблю повідомлень телемеханічних систем
- •Побудова кодів, які виявляють і виправляють помилки для заданого ансамблю повідомлень телемеханічних систем
- •Кодування циклічних кодів методами ділення інформаційних символів на утворюючий багаточлен та визначення провірочних символів під час проведення лінійни операцій
- •Декодування циклічних кодів з використанням схем ділення першого і другого типу
Визначення кількості інформації, оцінка інформаційних втрат та швидкості передачі для дискретних інформаційних каналів
6.1 Мета роботи
Вивчити визначення кількості інформації, оцінка інформаційних втрат та швидкості передачі для дискретних інформаційних каналів.
6.2 Варіанти завдань
6.2.1 При
частотній модуляції носійної неперервним
сигналом з рівномірним розподілом
частотна змінюється в межах
![]() МГц.
Визначити ентропію сигналу при вимірюванні
частоти із похибкою 5 кГц.
МГц.
Визначити ентропію сигналу при вимірюванні
частоти із похибкою 5 кГц.
6.2.2
Пропускна здатність неперервного каналу
С=9600 біт/с при відношенні
![]() .
Як зміниться С при зменшенні цього
відношення до 1?
.
Як зміниться С при зменшенні цього
відношення до 1?
6.2.3
Неперервний процес має нормальний
розподіл імовірностей із щільністю
![]() .
Визначити ентропію цього процесу при
похибці вимірювання
.
Визначити ентропію цього процесу при
похибці вимірювання
![]() .
.
6.2.4 При
частотній модуляції носійної неперервним
сигналом з рівномірним розподілом
частотна змінюється в межах
![]() МГц. Визначити ентропію сигналу при
вимірюванні частоти із похибкою 8 кГц.
МГц. Визначити ентропію сигналу при
вимірюванні частоти із похибкою 8 кГц.
6.2.5
Пропускна здатність неперервного каналу
С=1200 біт/с при відношенні
![]() .
Як зміниться С при зменшенні цього
відношення до 1?
.
Як зміниться С при зменшенні цього
відношення до 1?
6.2.6 Значення сигналу рівномірно лежить у діапазоні 0..10 В. Визначити диференційну ентропію цього джерела. Якою буде ця ентропія, якщо значення сигналу виразити в мілівольтах?
6.2.7 Телеметрична станція за 10 с передає покази 20 датчиків. Спектр частот неперервних повідомлень лежить у межах 0..30Гц. Рівень сигналів становить 0..10 В, а допустима відносна похибка дорівнює 0,5% його максимуму. Визначити потрібну швидкість передачі інформації в каналі.
6.2.8 Значення сигналу рівномірно лежить у діапазоні 0..20 В. Визначити диференційну ентропію цього джерела. Якою буде ця ентропія, якщо значення сигналу виразити в мілівольтах?
6.2.9 Телеметрична станція за 20 с передає покази 30 датчиків. Спектр частот неперервних повідомлень лежить у межах 0..60 Гц. Рівень сигналів становить 0..20 В, а допустима відносна похибка дорівнює 1% його максимуму. Визначити потрібну швидкість передачі інформації в каналі.
6.3 Основні теоретичні відомості
6.3.1 В
загальному випадку вважається, якщо
джерело
вибириє повідомлення
![]() ,
то це означає, що воно виробляє деяку
кількість інформації
,
то це означає, що воно виробляє деяку
кількість інформації
![]() .
.
Крім
того практично усі джерела виробляють
інформацію із плином часу, у цьому
випадку необхідно врахувати розподіл
ймовірностей
![]() ,
,![]() протягом
яких джерело вибирає повідомлення
протягом
яких джерело вибирає повідомлення
![]() .
.
Тоді одиниця вимірювання залежить від вибору 1 кількості інформації та 1 інтервалу часу (біт/с, бай/с).
В процесі функціонування джерело, як правило виробляє велику кількість повідомлень протягом часу спостереження, тому як загальну характеристикуджерела приймають середню за ансамблем його продуктивність користуючись відомими методом
![]() (6.1)
(6.1)
В
загальному випадку
![]() при
при![]() визначення продуктивності джерела щодо
певного повідомлення після усереднення
за часом можна перетворити до такого
визначення продуктивності джерела щодо
певного повідомлення після усереднення
за часом можна перетворити до такого
 ,
(6.2)
,
(6.2)
де
![]() – середній час вибору джерелом 1
повідомлення. Цей вираз дійсний і для
випадку коли джерело формує повідомлення
за один проміжок часу.
– середній час вибору джерелом 1
повідомлення. Цей вираз дійсний і для
випадку коли джерело формує повідомлення
за один проміжок часу.
Крім того із врахуванням отриманої формули загальна продуктивність джерела:
![]() (6.3)
(6.3)
Отже така характеристика, як продуктивність дискретного джерела інформації визначається його середнім показником ентропії, тобто середньою кількістю інформації в одному повідомленні та часом утворення такого повідомлення, якщо розглянути узагальнену модель будь – якої телемеханічної системи, що має вигляд
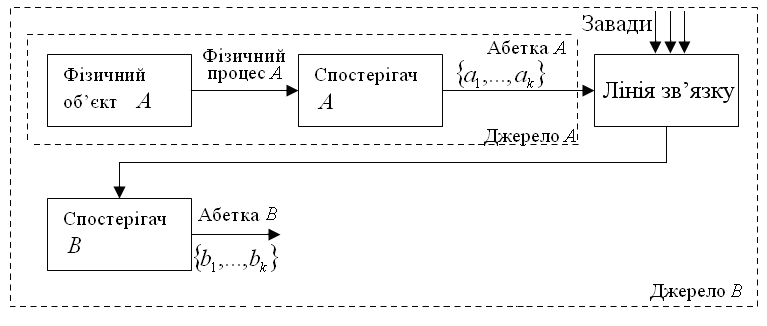
Оскільки повідомлення є множина і має певну форму (амплітудну, частотну, фазову, ітд.), то при передачі на лінію зв’язку впливають завади, що приводять до спотворення . Тому утворюється новий фізичний процес , що спорстерігається на вихідній лінії зв’язку, сама лінія при цьому розглядається, як деякий фізичний процес
Тоді
приймальний пристрій відіграє роль
спостерігача
,
який як джерело інформації утворює
повідомлення
![]() з деякої абетки джерела
відповідно до фізичного процесу лінії
зв’язку, тобто утворюється інше джерело
із своєю безумовною ентропією
з деякої абетки джерела
відповідно до фізичного процесу лінії
зв’язку, тобто утворюється інше джерело
із своєю безумовною ентропією
![]() при чому вибір повідомлення
із множини
характеризує процес передавання
інформації по лінії зв’язку від джерела
до
.
Якщо позначити через
при чому вибір повідомлення
із множини
характеризує процес передавання
інформації по лінії зв’язку від джерела
до
.
Якщо позначити через
![]() середню кількість інформації про стан
джерела
,
яка міститься в повідомленні джерела
,
якщо на вибір кожного повідомлення
затрачається час
середню кількість інформації про стан
джерела
,
яка міститься в повідомленні джерела
,
якщо на вибір кожного повідомлення
затрачається час
![]() ,
то питома кількість є швидкістю
передавання інформації по каналу
,
то питома кількість є швидкістю
передавання інформації по каналу
![]() (6.4)
(6.4)
6.3.2 Інформаційні втрати при передачі даних по дискретному каналу
Основною
задачею будь – якого дискретного джерела
є забезпечення однозначної відповідності
повідомлень
та
![]() це можливо коли
це можливо коли
![]() (6.5)
(6.5)
Для всіх
![]() ,
а це означає, що мають виконуватися такі
рівності
,
а це означає, що мають виконуватися такі
рівності
![]()
![]() (6.6)
(6.6)
![]()
Такий
випадок можливий тоді коли в каналі
обміну даних завади не приводять до
спотворення тобто є повний збіг ансамблів
та
,
якщо канал такий то середня кількість
інформації на одне повідомлення
![]() при повній відсутності інформаційних
втрат рівна тій же кількості інформації
при повній відсутності інформаційних
втрат рівна тій же кількості інформації
![]() ,
тобто
,
тобто
![]() (6.7)
(6.7)
Тому кількість переданої інформації за відсутності завад дорівнює ентропії джерела та , або безумовній ентропії одного із джерел.
У випадку значних завад джерела та стають статистично незалежними тоді всі повідомлення ніяк статистично не зумовлені повідомлення тоді маємо:
![]()
![]() (6.8)
(6.8)
У цьому випадку ентропія об’єднання двох джерел
![]() (6.9)
(6.9)
тобто
жодна інформація джерела
та
непередається внаслідок її повного
спотворення. Інформаційною мірою такого
спотворення є умовна ентропія одного
джерела відносно іншого, що збільшується
від 0 до
![]() у міру зростання статистичної зумовленості
джерела
.
У проміжному випадку тобто коли у джерелі
виявляють деяку статистичну залежність,
а заводи спотворюють частково, що
відображаються у вигляді матриці
ймовірносних переходів тоді умовна
ентропія має обмеження.
у міру зростання статистичної зумовленості
джерела
.
У проміжному випадку тобто коли у джерелі
виявляють деяку статистичну залежність,
а заводи спотворюють частково, що
відображаються у вигляді матриці
ймовірносних переходів тоді умовна
ентропія має обмеження.
![]()
![]()
Отже,
якщо джерело
обрало певне повідомення то воно виробляє
певну інформацію, що дорівнює
![]() джерела
за умови порушення статистичної
залежності джерела
та
обирає деяку кількість інформації про
джерело
,
що є в джерелі
джерела
за умови порушення статистичної
залежності джерела
та
обирає деяку кількість інформації про
джерело
,
що є в джерелі
![]() .
.
Приймальний
пристрій
обравши повідомлення
![]() із множини
приймає рішення про отримане повідомлення
із множини
.
Прийнявши це рішення він виробляє таку
кількість інформації про джерело
внаслідок чого кількість інформації
про джерело
визначається, як кількість нового
відсутнього знання про це джерело
різницею:
із множини
приймає рішення про отримане повідомлення
із множини
.
Прийнявши це рішення він виробляє таку
кількість інформації про джерело
внаслідок чого кількість інформації
про джерело
визначається, як кількість нового
відсутнього знання про це джерело
різницею:
![]()
За умови значного рівня завад:
![]() (6.10)
(6.10)
По аналогії можна записати:
![]()
тобто
![]()
звідси
![]() (6.11)
(6.11)
Таким чином інформаційні втрати при передачі даних в каналі визначається умовною ентропією джерела відносно іншого, а кількість переданої інформації безумовною ентропією та інформаційними втратами тому можна записати
![]()
![]()
6.3.3 Пропускна здатність
Максимально можлива швидкість передачі інформації по каналу зв’язку називається пропускною здатністю.
![]() (6.12)
(6.12)
Даний вираз досягає максимального значення у випадку абсолютного статистично залежних джерел тобто коли завади відсутні або несуттєві тоді
![]() (6.13)
(6.13)
Як було раніше згадано безумовна ентропія джерела досягається у випадку при рівноймовірних і статистично незалежних повідомлень , тобто
![]() (6.14)
(6.14)
де
![]() – кількість станів, тоді
– кількість станів, тоді
![]() – пропускна
здатність каналу без завад.
– пропускна
здатність каналу без завад.
Якщо в каналі є відчутні завади то його умовна ентропія зростає і пропускна здатність зменшується
![]() (6.15)
(6.15)
При зростанні завад вираз прямує до 0, а при зменшенні до
6.4 Порядок виконання робіт циклу
6.4.1 Ознайомитися із метою лабораторної роботи та основними теоретичними відомостями.
6.4.2 Одержати у викладача завдання.
6.4.3 Використовуючи програми Exell або MathCad: виконати завдання.
6.5 Контрольні питання
6.5.1 Що таке ентропія неперервного джерела?
6.5.2 Що таке диференціальна ентропія неперервного джерела?
6.5.3 Як обчислюється диференціальна ентропія неперер-вного джерела?
6.5.4 Як визначити кількість інформації на одне повідомлення неперервного джерела?
6.5.5 За яких умов диференціальна ентропія неперервного джерела буде від’ємною?
6.5.6. Що означає відносність диференціальна ентропія неперервного джерела?
6.5.7 Як визначається пропускна здатність непервного джерела?
Лабораторна робота №7
Побудова кодових комбінацій n – розрядних кодів для
кодування повідомлень в телемеханічних системах,
мінімальна та максимальна кодова відстань
7.1 Мета роботи
Вивчення принципів побудови кодових комбінацій n – розрядних кодів для кодування повідомлень в телемеханічних системах, мінімальна та максимальна кодова відстань.
7.2 Варіанти завдань
7.2.1 Записати десяткове число 333 у двійковій системі числення.
7.2.2 Записати десяткове число 222 у двійковій системі числення.
7.2.3 Записати десяткове число 397 у двійковій системі числення.
7.2.4 Записати десяткове число 4327 у шістнадцятковій системі числення.
7.2.5 Записати десяткове число 3689 у шістнадцятковій системі числення.
7.2.6 Записати десяткове число 5132 у шістнадцятковій системі числення.
7.2.7
Визначити мінімальну та максимальну
кодові відстані
![]() Хеммінга між комбінаціями двійкового
простого коду, вказавши на пари комбінацій
з
Хеммінга між комбінаціями двійкового
простого коду, вказавши на пари комбінацій
з
![]() та
та
![]() для комбінацій 000011, 110111, 010100, 101001, 011101.
для комбінацій 000011, 110111, 010100, 101001, 011101.
7.2.8 Визначити мінімальну та максимальну кодові відстані Хеммінга між комбінаціями двійкового простого коду, вказавши на пари комбінацій з та для комбінацій 011000, 100111, 000100, 100001, 011101.
7.2.9 Визначити мінімальну та максимальну кодові відстані Хеммінга між комбінаціями двійкового простого коду, вказавши на пари комбінацій з та для комбінацій 110011, 000111, 000100, 001001, 010101.
7.2.10 Визначити кодову відстань між такими комбінаціями.
7.3 Основні теоретичні відомості
Кодування – це процес перетворення повідомлення на впорядкований набір символів, знаків, тощо.
При кодуванні кожному повідомленні ставиться у відповідність зумовлена кодова комбінація тобто набір символів з деякої обмеженої множини, яку називають абеткою.
Кодом – множина комбінацій символів побудованих за одним правилом в залежності від заданої абетки код розділяється на двійкові (абетка складається із двох символів 0 і 1), багатопозиційні (недвійкові) абетка, яких налічує більше двох символів. Крім того всі коди ділять на такі групи:
безнадмірні (первинні, прості),
надмірні (кориткувальні, завадостійкі).
Безнадмірні коди є високоефективними, щодо інформації ємності але не дозволяють виявляти спотворення повідомлень.
Надмірні мають меншу інформаційну ємність але можуть виявляти і/або виправляти елементи кодових послідовностей спотворених впливом завад.
Крім того обидві групи кодів повідомлень на :
- рівномірні
- не рівномірні
Рівномірні передбачають сталу кількість розядів в кожному повідомленні, а нерівномірні змінну кількість.
Надмірні коди бувають:
не перервними
блоковими
В неперервних кодах процес кодування та декодування має неперервний характер.
Блокові коди є:
) неподільні
) подільні – коди, що будуються доповненням інформаційних елементів перевірними елементами. Вони бувають:
систематичні – це код в комбінації якого перші позицій займають інформаційні елементи, а решту
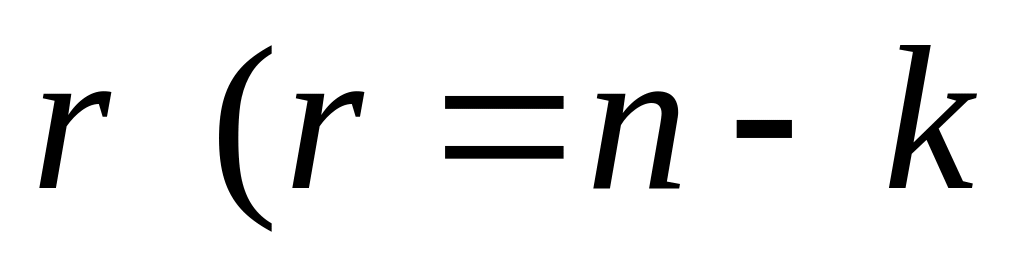 ,
де
– загальна кількість позицій) перевірні
коди.
,
де
– загальна кількість позицій) перевірні
коди.не систематичні коди – це коди в яких інформаційні елементи не займають перших позицій, а можуть бути розміщені по всій довжині повідомлення.
При виборі коду для передачі інформації керуються вимогами, щодо вірогідності та швидкості передачі, що визначається такими характерами:
кількістю інформаційних елементів
кількістю
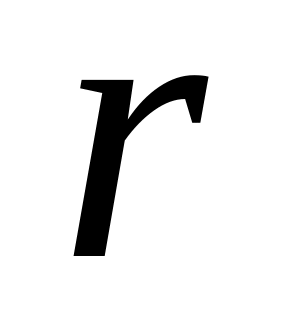 перевірних елементів
перевірних елементівдовжиною або загальною кількістю , що входять до складу кодової комбінації.
основою або абеткою
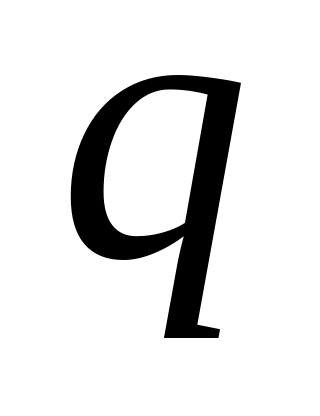 .
.потужністю
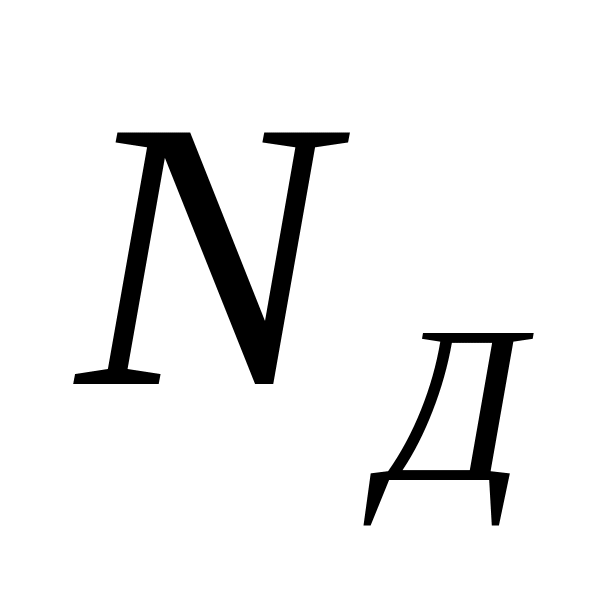 або кількістю дозволених кодових
комбінацій, що використовуються для
передачі повідомлень.
або кількістю дозволених кодових
комбінацій, що використовуються для
передачі повідомлень.повною кількістю
 кодових комбінацій (кількістю усіх
можливих комбінацій, яка для двійкових
систем визначається так
,
а для всіх інших
кодових комбінацій (кількістю усіх
можливих комбінацій, яка для двійкових
систем визначається так
,
а для всіх інших
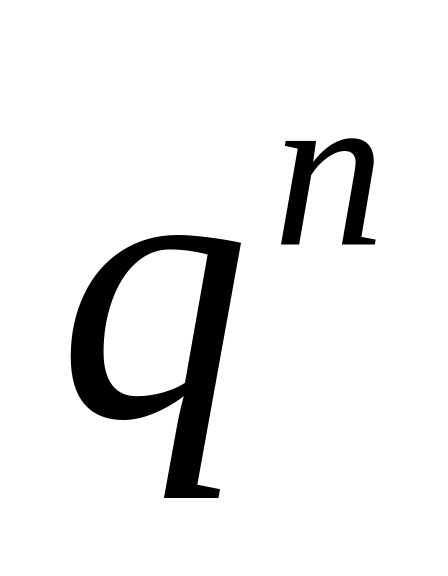 )
)надмірністю для неподільних кодів двійкової системи:
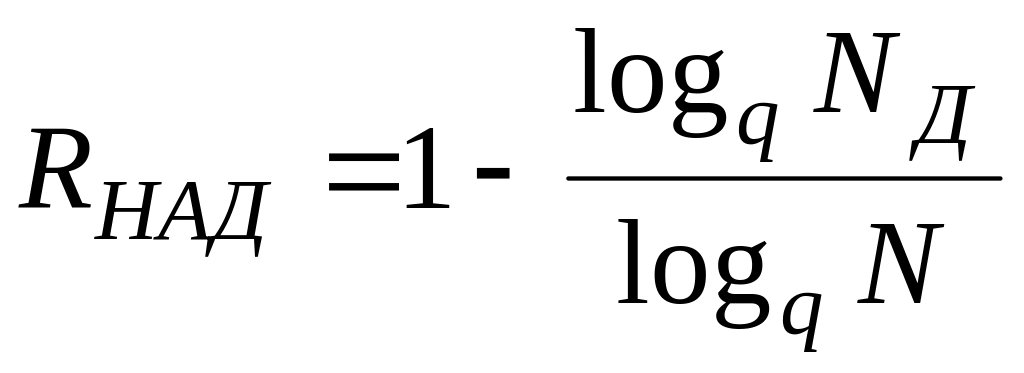 ,
(7.1)
,
(7.1)
а для подільних кодів двійкової системи:
![]() (7.2)
(7.2)
відносною швидкістю
 ,
що характеризує ступінь використання
в надмірному коді інформаційних
можливостей його потужності:
,
що характеризує ступінь використання
в надмірному коді інформаційних
можливостей його потужності:
![]() (7.3)
(7.3)
![]() (7.4)
(7.4)
мінімальною кодовою відстанню
 або мінімальною відстанню між парами
наявними кодових комбінацій:
або мінімальною відстанню між парами
наявними кодових комбінацій:
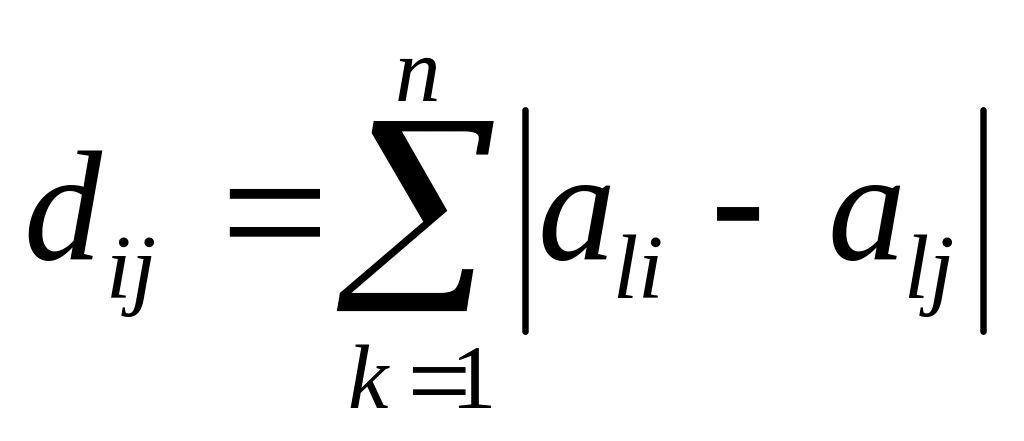 ,
(7.5)
,
(7.5)
де
![]() ,
,
![]() – елементи, що знаходяться в
– елементи, що знаходяться в
![]() –
му місці в
–
му місці в
![]() та
та
![]() кодовій комбінації тобто де
кодовій комбінації тобто де
![]() визначається кількістю одноіменних
розрядів із різними значеннями.
визначається кількістю одноіменних
розрядів із різними значеннями.
імовірністю невиявленої помилки, тобто імовірністю такої події за якої прийнята комбінація відрізняється від відправленої але властивості коду не дають це визначити.
ймовірністю виявленої помилки тобто ймовірністю, що прийнята кодова комбінація відрізняється від відправленої і властивості коду дають виявити цей факт.
ймовірністю виправленої помилки тобто ймовірністю події якої прийнята кодова комбінація відрізняється від відправленої і властивості коду дають можливість виправити помилкую
ймовірністю виникнення помилки тобто ймовірністю події за якої передана кодова комбінація буде відрізнятися від отриманої для кодів, які виявляють помилки:
![]() (7.6)
(7.6)
а для кодів, які виправляють помилки:
![]() (7.7)
(7.7)
кратність помилки
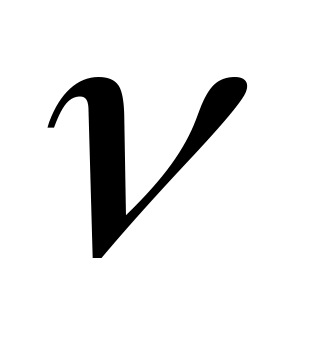 –
що визначається кратністю виявлених
та кратністю виправлених помилок
–
що визначається кратністю виявлених
та кратністю виправлених помилокефективність
 .
(7.8)
.
(7.8)
7.4 Порядок виконання робіт циклу
7.4.1 Ознайомитися із метою лабораторної роботи та основними теоретичними відомостями.
7.4.2 Одержати у викладача завдання.
7.4.3 Використовуючи програми Exell або MathCad: виконати завдання.
7.5 Контрольні питання
7.5.1 Що таке кодування?
7.5.2 Що таке код?
7.5.3 На які групи ділять коди?
7.5.4 Як розраховують мінімальну кодову відстань?
7.5.5 Якими бувають надмірні коди?
7.5.6 Що таке надмірність коду?
7.5.7 Як розраховують ймовірність виникнення помилок?
7.5.8 Як розраховується ефективність?
Лабораторна робота №8
