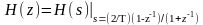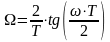ЛАБОРАТОРНА РОБОТА №2
ПРОЕКТУВАННЯ ЦИФРОВОГО БІХ-ФІЛЬТРУ МЕТОДОМ БІЛІНІЙНОГО ПЕРЕТВОРЕННЯ В ПАКЕТІ ПРОГРАМ MATLAB
Мета роботи
1. Вивчити особливості синтезу БІХ-фільтрів методом білінійного перетворення в пакеті програм MATLAB;
2. Синтезувати цифровий фільтр методом білінійного перетворення;
3. Дослідити характеристики синтезованого цифрового фільтру.
Короткі теоретичні відомості
1. Метод білінійного перетворення
Метод білінійного перетворення відноситься до аналітичних методів розрахунку.
По методу білінійного перетворення ЦФ, що синтезується, ставиться у відповідність деякий аналоговий фільтр-прототип (АФП) з передатною функцією Н(s) і частотною характеристикою H(jΩ), однозначно пов'язаними з передатною функцією H(z) і частотною характеристикою H(jω) ЦФ:
АФП ЦФ АФП ЦФ
Зв'язок цей визначається прямою s = f(z) і зворотною z = f-1(s) перетворюючими функціями і відповідні ним при s = jΩ і z = ejωTд перетвореннями частот Ω = f(ω), ω = f - 1(Ω) аналогового і цифрового фільтрів.
За допомогою цих перетворень визначаються вимоги до АФП, по яких розробленими методами синтезується його передатна функція H(s), що перетворюється потім в шукану передатну функцію ЦФ H (z).
Білінійне перетворення, яке визначається таким чином:
S = f (z) = (2/T)[(1 - z - 1) / (1+z - 1)] |
(2.1) |
Можна також знайти зворотне співвідношення
z – 1 = [ (2 - sT) / (2+sT)] |
(2.2) |
З властивостей процедури переходу на основі білінійного перетворення витікає, що уявна вісь S-площини відображається в одиничне коло в Z-площини (де |z|=1).
Білінійне перетворення - однозначна функція. Це означає, що кожній точці в Z-площини відповідає одна точка в s-площині і навпаки. З цієї властивості однозначності виходить, що відсутній ефект накладання спектрів при білінійній процедурі відображення.
Методика розрахунку цифрових фільтрів на основі методу білінійного перетворення включає знаходження відповідної передатної функції Н(s) аналогового фільтру і застосування до неї білінійного перетворення для отримання передатної фікції H(z) потрібного цифрового фільтру
|
(2.3) |
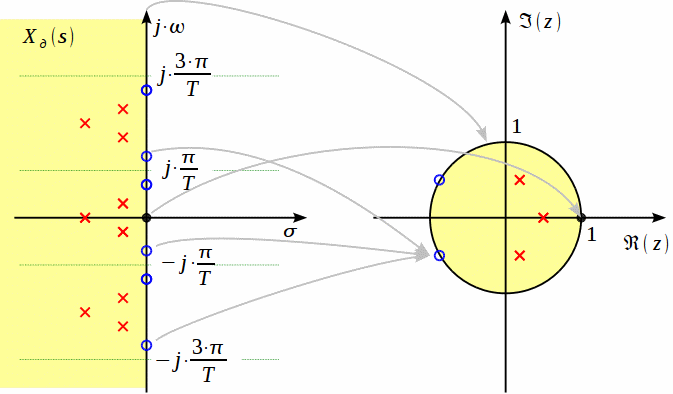
Рис. 2.1. Властивості процедури переходу на основі білінійного перетворення
При цьому перетворенні зберігатимуться і частотні характеристики, і властивості стійкості аналогового фільтру. Проте це не означає, що частотні характеристики аналогового і цифрового фільтру ідентичні, однакова тільки їх «форма». Наприклад, якщо амплітудно-частотна характеристика аналогового фільтру монотонно спадає при 0 < < , то відповідний цифровий фільтр, отриманий за допомогою співвідношення (2.3), володітиме монотонно спадаючою АЧХ при 0 < < ,. Тобто, якщо АЧХ аналогового фільтру має k підйомів і спадів при 0 < < , то і амплітудно-частотна характеристика відповідного цифрового фільтру матиме k підйомів і спадів.
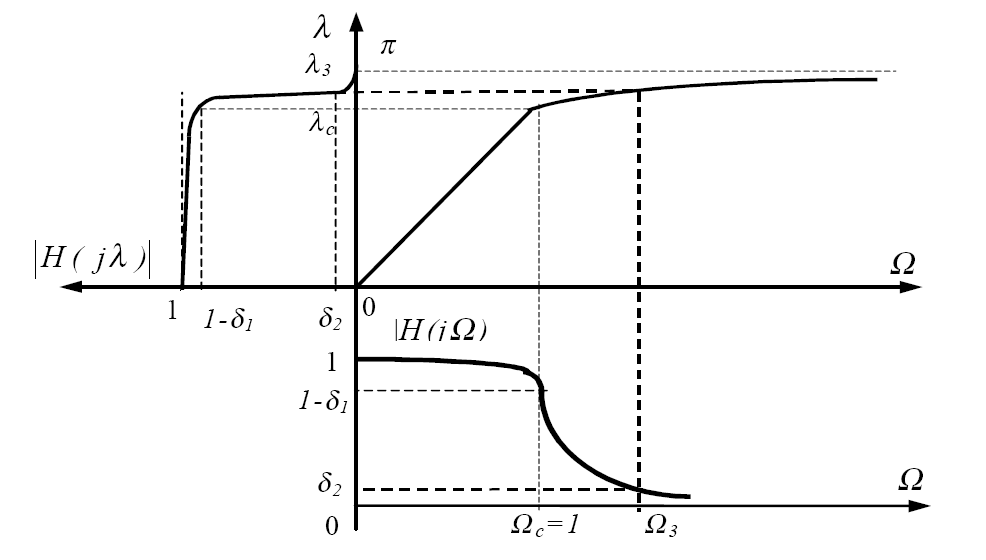
Рис. 2.2. Перетворення АЧХ аналогового ФНЧ в АЧХ цифрового ФНЧ
В результаті переходу до нормованих частот ЦФ частотні перетворення приймають вигляд
|
(2.4) |
Характер деформації частот при білінійному перетворенні показаний на рис. 2.2.
Для
забезпечення рівності
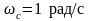необхідно деформувати частоту аналогового
ФНЧ - прототипу:
.
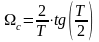Білінійне перетворення забезпечує просту процедуру переходу від аналогових до цифрових фільтрів і зберігає вид частотних характеристик при перетворенні. Це означає, що широкосмугові аналогові фільтри з крутою перехідною областю відображаються в широкосмугові цифрові фільтри без ефекту накладання. У цьому полягає основна перевага цього методу в порівнянні з методом інваріантності імпульсної характеристики. Недоліком білінійного перетворення є те, що нелінійність співвідношення між цифровою частотою і аналоговою частотою Ω призводить до спотворення частотних характеристик аналогових фільтрів. Крім того, при цьому перетворенні не зберігається імпульсна характеристика.