2.4.3. Зв'язок між коефіцієнтом кореляції та нахилом b1

Звичайно, нас цікавить, чи є зв'язок між коефіцієнтом кореляції та детермінації, і якщо є, то який? Перш ніж відповісти на це запитання, розглянемо зв'язок між коефіцієнтом кореляції та нахилом регресійної лінії, тобто параметром b₁. Нагадаємо формули для розрахунків коефіцієнта кореляції та нахилу:

(2.35)

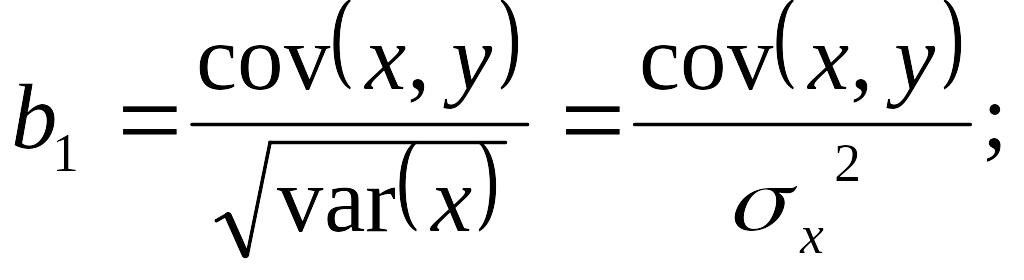(2.36)

Вираз (2.35) може бути переписаний у вигляді:

(2.37)

З того, що обидва значення і додатні, випливає, що знак коефіцієнта кореляції r завжди збігається із знаком параметра b₁. Крім того, з (2.37) випливає, що значення коефіцієнта кореляції (r) пов'язане із значеннями нахилу b₁ та середніх квадратичних відхилень і .

2.4.4. Зв'язок між коефіцієнтом кореляції (г) і коефіцієнтом детермінації (r2)

Знаючи зв'язок між коефіцієнтом кореляції та нахилом регресійної лінії, розглянемо зв'язок між коефіцієнтом кореляції та детермінації. Нагадаємо формулу для розрахунку коефіцієнта детермінації:

(2.38)

Нагадаємо також, що:

(2.39)

(2.40)

Перепишемо (2.40) у такому вигляді:

(2.41)

Внесемо зміни до (2.38), враховуючи (2.39) і (2.41). Отримаємо:

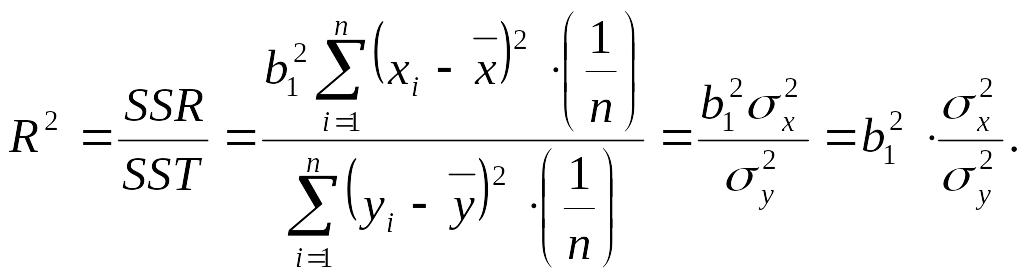(2.42)

3 (2.37) маємо:

Отже, порівнюючи вирази (2.37) та (2.42), встановлюємо, що коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції:

(2.43)

Для ілюстрації наведених викладок повернемося до нашого прикладу. За наведеними раніше даними, розрахуємо коефіцієнт кореляції та детермінації, скориставшись табл. 2.5.

Таблиця 2.5

i	yi	xi	xi2	xiyi
1	25	5	25	125	-15	225	25	0	225
2	30	6	36	180	-10	100	28	4	144
3	35	9	81	315	-5	25	37	4	9
4	45	12	144	540	5	25	46	1	36
5	65	18	324	1170	25	625	64	1	576
	200	50	610	2330	0	1000		10	990
/n	40	10	122	466	0	200

b₁=3; b₀=10.

y=3x+10;

2.4.5. Перевірка простої регресійної моделі на адекватність. Поняття f-крітеріюФішера.

Раніше ми показали, що адекватність простої лінійної регресійної моделі можна перевірити за допомогою коефіцієнта детермінації. Якщо його значення близьке до одиниці, то можна вважати, що модель адекватна. Якщо його значення близьке до нуля, то модель неадекватна, тобто не має лінійного зв'язку між залежною та незалежною змінними. Але який висновок можна зробити, якщо значення коефіцієнта кореляції має нечітко виражене граничне значення, наприклад 0.5, 0.45, 0.44 і т. ін. Зрозуміло, що в таких випадках важко зробити однозначний висновок про наявність зв'язку, тобто про адекватність моделі. Потрібен інший критерій, який би однозначно відповідав на питання про адекватність побудованої моделі. Найпоширенішим з таких критеріїв є критерій Фішера. Розглянемо, як він утворюється. Для цього повернемося до простої регресійної моделі:

(2.46)

На підставі тільки того, що до правої частини (2.46) входить випадкова величина е₁, уже можна зробити висновок, що величини y_i будуть також випадковими. Будь-яка функція від них буде також випадковою. Запам'ятаємо цей факт і повернемось ще раз до таблиці ANOVA-дисперсійного аналізу. Розглянемо:

(2.47)

(2.48)

Як бачимо, середні квадрати MRS і MSE є функціями від залежних змінних, тому також будуть випадковими величинами, тобто матимуть свій розподіл, математичне сподівання, дисперсію та моменти.

З теорії імовірностей відомо (ми цей факт детально не розглядатимемо, а відсилаємо читача до математичного додатка цього підручника), що величина

(2.49)

має функцію розподілу F з {(1 та (п-2)} ступенями вільності у разі простої лінійної регресії) за умови, що нахил узагальненої моделі дорівнює нулеві, тобто . (Що таке узагальнена модель і чому ми вводимо та — пояснимо трохи пізніше). На цьому базується F-критерій Фішера, який дозволяє оцінити, чи значно нахил b₁ відрізняється від нуля, тобто перевірити побудовану модель на адекватність. Пояснимо цей факт. Справді, якщо оцінка нахилу b₁ незначно відрізняється від нуля, тоді:

(2.50)

за умови, що .

Отже, вираз (2.50) дає змогу по-іншому інтерпретувати критерій Фішера. Він дозволяє перевірити базову гіпотезу (в статистиці вона називається нульовою гіпотезою (H₀), що краще апроксимувати дані середнім значенням , ніж регресійною прямою . Це в свою чергу і дає змогу перевірити наявність або відсутність лінійного зв'язку між змінними, іншими словами, адекватність побудованої регресійної моделі реальній дійсності.

Перевірка моделі на адекватність за F-критерієм Фішера передбачає здійснення певних етапів:

На першому етапі розраховуємо величину так званого F -відношення:

де MSR — середній квадрат, який можна пояснити з регресійної моделі;

MSE — середній квадрат помилок; 1, (n-2) — ступені вільності, відповідно пов'язані з MSR і MSE.

2. На другому етапі задаємо рівень значимості або . Наприклад, якщо ми вважаємо, що можлива помилка для нас становить 0.05 (або 5%), це означає, що ми можемо помилитися не більше ніж у 5% випадків, а в 95% випадків наші висновки будуть правильними.

3. На третьому етапі за статистичними таблицями .F-розподілу Фішера з (1,n-2) ступенями вільності і рівнем значимості обчислимо критичне значення (F).

4. Якщо розраховане нами значення F>F_кр , то ми відкидаємо гіпотезу Н₀, що (або що з ризиком помилитися не більше ніж у 5% випадків.

Отже, якщо F>F_кр,, то побудована нами регресійна модель адекватна реальній дійсності.

Повернемося до нашого прикладу. Перевіримо розраховану раніше модель на адекватність за F-критерієм Фішера. Використаємо для цього дані табл. 2.8.

Таблиця 2.8

і	yi
1	25	25	0	225
2	30	28	4	144
3	35	37	4	9
4	45	46	1	36
5	65	64	1	576
£	200		10	990

За табл. 2.8 і за таблицями ANOVA-дисперсійного аналізу (2;6) і (2.7), знайдемо середній квадрат, що пояснює регресію, та середній квадрат помилок:

Використовуючи значення середніх квадратів, обчислимо F-відношення Фішера:

За таблицею F-розподілу знаходимо критичне значення F_кр з 1 та 3 ступенями вільності, задавши попередньо рівень довіри 95% або рівень значимості (помилки) 5%. Це буде точка F_{(1;3;0,95)кр}=10.13.

Розраховане значення F_(1,3)=300; а табличне значення F_{(1;3;0,95)кр}=10.13.

Отже, F>F_кр , що дозволяє зробити висновок про адекватність побудованої моделі реальній дійсності.