2. Основні задачі статистичного моделювання

2.1. Загальне поняття про лінійну регресію

Прості лінійні регресійні моделі встановлюють лінійну залежність між. двома змінними, наприклад витратами на рекламу та обсягом продукції, що випускається та інші [8]. При цьому одна із змінних вважається залежною змінною (у) та розглядається як функція від незалежної змінної (х).

У загальному вигляді проста вибіркова регресійна модель запишеться так:

у=b₀+b₁x+e (2.1)

де у — вектор спостережень за залежною змінною; у={у₁,у₂,...,у_n};

х — вектор спостережень за незалежною змінною; х={х₁,х₂,...,х_n};

b₀,b₁— невідомі параметри регресійної моделі;

e — вектор випадкових величин (помилок); е={е₁,е₂,...,е_n}.

Регресійна модель називається лінійною, якщо вона лінійна за своїми параметрами. Отже, модель (2.1) є лінійною регресійною моделлю. Її ще можна трактувати і як пряму на площині, де b₀ — перетин з віссю ординат, a b₁ - нахил (звичайно, якщо абстрагуватися від випадкової величини е).

2.2. Оцінка параметрів лінійної регресії за допомогою методу найменших квадратів

Щоб мати явний вид залежності, необхідно знайти (оцінити) невідомі параметри b₀, b₁ цієї моделі. Як це зробити? Яким критерієм краще користуватися? Щоб відповісти на ці запитання, розглянемо спочатку приклад.

Приклад. Бюро економічного аналізу фабрики "Світоч" оцінює ефективність відділу маркетингу з продажу. Для такої оцінки вони мають досвід праці у 5 географічних зонах з майже однаковими умовами (потенційні клієнти, ставлення до товарного знака і т. ін.). У цих зонах вони зафіксували протягом однакового періоду обсяги продажів (млн. шт.), витрати (млн. грн.) фірми та просування товару на ринку. Дані наведені в табл.2.1.

Реальні спостереження у_i зобразимо точками у системі координат (X,Y) (рис.2.1).

Рис. 2.1.Залежність між обсягами продажу продукції та витратами на рекламу

Візуально можна припустити, що між даними є лінійна залежність, тобто їх можна апроксимувати прямою лінією.

Таблиця 2.1

І	yi	xi
1	25	5
2	30	6
3	35	9
4	45	12
5	65	18

Взагалі, існує необмежена кількість прямих у=b₀+b₁x, які можна провести через множину спостережуваних точок. Яку ж із них вибрати?

Щоб це визначити, потрібно мати у розпорядженні певний критерій, що дозволяв би вибрати з множини можливих прямих "найкращу" з точки зору даного критерію. Найпоширенішим є критерій мінімізації суми квадратів відхилень. На Рис. 2.1, наприклад, пряма (1), як і інші, розташована таким чином, що деякі точки знаходяться вище, деякі нижче цієї прямої, на основі чого можна встановити відхилення (помилки) відносно цієї прямої:

(2.2)

де — і-та точка на прямій, яка відповідає значенню х_i (див. рис. 2.2).

Рис. 2.2. Відхилення теоретичних значень від фактичних

Відхилення, або помилки, ще інколи називають залишками. Логічно, що треба проводити пряму таким чином, щоб сума квадратів помилок була мінімальною. В цьому і полягає критерій найменших квадратів: невідомі параметри b₀ та b₁ визначаються таким чином, щоб мінімізувати .

Справді, за критерієм маємо

(2.3)

Визначимо значення b₀ та b₁ які мінімізують вираз (2.3). Мінімум функції (2.3) досягається за необхідних умов, коли перші похідні дорівнюють нулеві, тобто

(2.4)

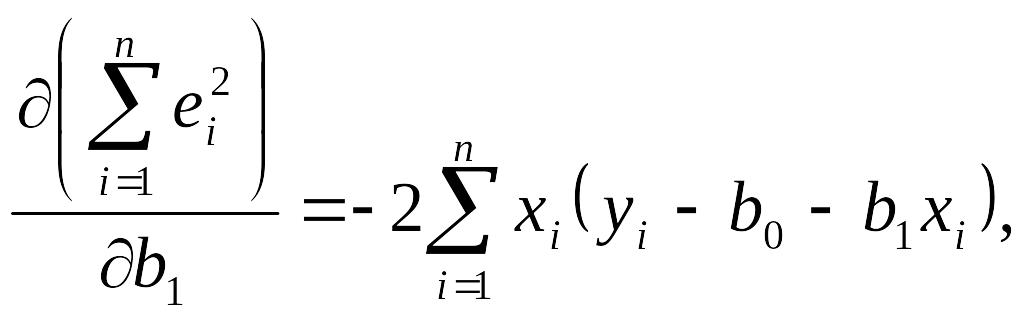(2.5)

звідки отримаємо систему лінійних рівнянь:

(2.6)

яка називається нормальною. Розв'язок (2.6) відносно нахилу прямої (невідома b₁) дає

(2.7)

З метою спрощення виразу для b₁ чисельник та знаменник виразу 2.7 помножимо на 1/n.

Отримаємо:

(2.8)

де

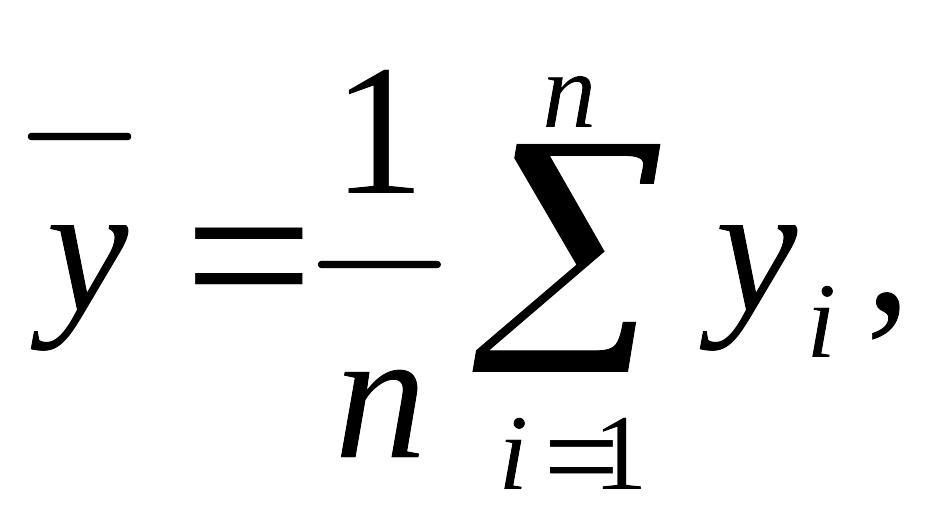
Вираз (2.8) можна записати ще таким чином:

(2.9)

Справді,

(2.l0)

(2.ll)

Чисельник (2.9) є не що інше, як коефіцієнт коваріації між х та у. За означенням, коефіцієнт коваріації між двома змінними х та у визначається за формулою:

(2.12)

Знаменник (2.9) є дисперсією величини х, тобто

(2.13)

Отже, кут нахилу прямої регресії можна встановити як за формулою (2.7), так і за формулами (2.8) та (2.9).

Для визначення параметра b₀ повернемося до (2.5). Маємо:

(2.14)⁾

Вираз (2.14) дає нам, по-перше, підтвердження того, що сума помилок дорівнює нулеві. Справді,

(2.15)

по-друге, розділивши (2.14) на п, маємо вираз для визначення b₀:

(2.16)

Таким чином, ми знайшли формули для визначення невідомих параметрів &д та Ь , і можемо записати у явному вигляді регресію у від х, у якій параметри обчислені за методом найменших квадратів. Її інколи називають регресією найменших квадратів у від х. Маємо:

(2.17)

або

(2.18)

Для ілюстрації цих викладок повернемося до нашого прикладу про дослідження ефективності витрат на рекламу. Проведені попередні розрахунки подамо у вигляді табл. 2.2.

Для обчислення невідомих параметрів b₀ , b₁ необхідно послідовно здійснити такі розрахунки:

Таблиця 2.2

I	yi	xi	xi2	xi yi
1	25	5	25	125
2	30	6	36	180
3	35	9	81	315
4	45	12	144	540
5	65	18	324	1170
Z	200	50	610	2330
/n	40	10	122	466

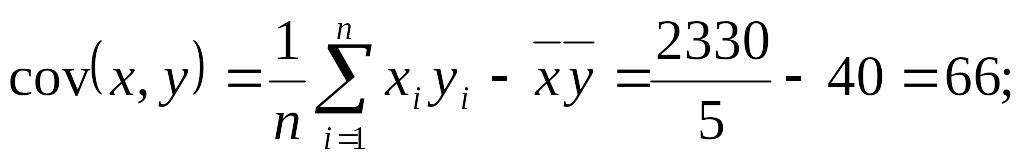
Знаючи параметри b₀ b₁, отриману пряму запишемо у вигляді:

.

Таблиця 2.4

	xi	yi	xiyi	xi2
	1	16	16	1	14.74	1.26
	2	12	24	4	17.37	-5.37
	2	23	46	4	17.37	5.63
	4	19	76	16	22.63	-3.63
	6	30	180	36	27.89	2.11
Всього	15	100	342	61	100	0

Рис. 2.3. Залежність витрат на відпустку від кількості членів родини

Отже, маємо:

(2.19)

Рівняння (2.19) дає для кожного спостережуваного значення x_i. значення та е_i (дві останні колонки табл. 2.4). Підкреслимо, що сума оцінених значень дорівнює сумі фактичних значень у_i, а сума помилок дорівнює нулеві.