4.2. Еквівалентність матричної гри пар і задач лінійного програмування

Нехай задано матричну гру двох партнерів з нульовою сумою платіжною матрицею

(4.9)

і множинами змішаних стратегій {P} {Q}.

Лема 4.1. Ціну матричної гри. можна змінити на довільне, наперед задане число додавши його до всіх елементів платіжної матриці, не змінюючи при цьому розв'язку гри.

Доведення. Нехай ціна гри, заданої платіжною матрицею (4.9), дорівнює с, а її розв'язок (р*,q*). Розглянемо гру, яка задана платіжною матрицею (4.9а) і множинами змішаних стратегій {Р} і {Q}, що збігаються з відповідними множинами попередньої задачі

(4.9а)

де .Визначаючи ціну цієї гри b, дістанемо:

(4.10)

що й треба було довести.

Доведена лема дає змогу приписувати ціні гри певний знак, наприклад додатний. Справді, проводячи деякі обчислення, пов'язані з ціною гри, завжди можна спочатку збільшити її величину на довільне додатне число 9 так, щоб нова ціна гри с була додатна, а, закінчивши обчислення, справжнє значення ціни гри легко встановити, віднявши 9 від знайденого значення ціни гри.

Припустимо тепер, що другий гравець застосовує свою j-ту чисту стратегію, і обчислимо математичне сподівання виграшу першого гравця при застосуванні ним деякої змішаної стратегії р:

(4.11)

Поставимо тепер питання про відшукання оптимальної змішаної стратегії першого гравця р* при умові, що його партнер застосовує оптимальну змішану стратегію q*, тобто про відшукання максимуму такої величини:

` (4.12)

Внаслідок оптимальності стратегії q* всі величини (4.11) при довільній стратегії р* не менші від величини (4.12), тобто

(4.13)

Приєднуючи до цього умову

p₁+p₂+…+p_m=1, ` (4.14)

бачимо, що дістали задачу лінійного програмування на максимізацію цільової функції (4.12) при системі умов (4.13), (4.14) і змінних

і (4.15)

Користуючись доведеною лемою, задачу (4.12)—(4.15) можна звести до зручнішої форми.

Вважаючи внаслідок доведеної леми а(р,q*)>0, поділимо обидві частини останніх нерівностей (4.13) на цю величину. Позначаючи

(4.16)

дістанемо вирази:

(4.17)

Поділивши на а(р,q*) обидві частини рівності (4.14) і позначивши

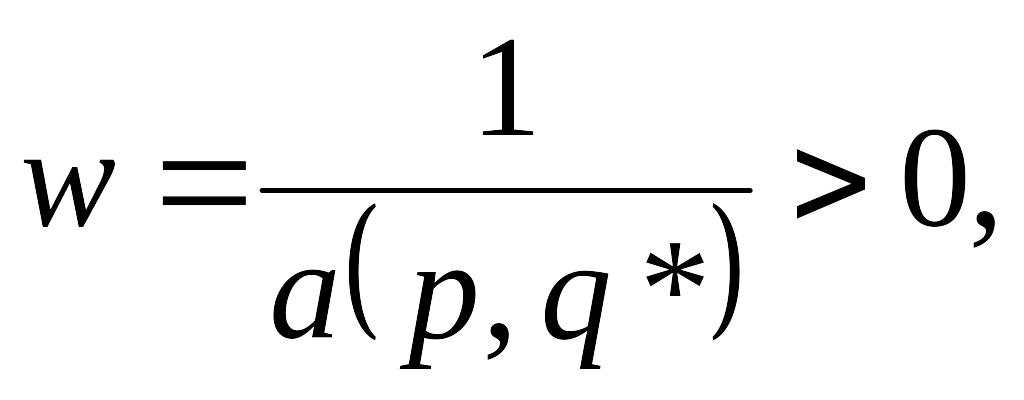(4.18)

дістанемо такий виразі

w=y₁+y₂+…+y_m (4.19)

Очевидно, що задача мінімізації лінійної форми (4.19) при системі умов (4.16)—(4.18) еквівалентна попередній задачі максимізачії лінійної форми (4.12) при системі умов (4.13)—(4.15).

Цим самим доведено, що задача відшукання оптимальної стратегії першого гравця р* при відомій оптимальній стратегії другого гравця q* рівнозначна задачі лінійного програмування (4.16)—(4.19) або (4.12)—(4.15).

Міркуючи аналогічно, прийдемо до іншої задачі лінійного програмування, розв'язок якої дає оптимальну стратегію другого гравця q* при умові визначеності оптимальної стратегії першого р*:

(4.20)

(4.21)

(4.22)

(4.23)

Зробивши таку заміну змінних

(4.24)

і вважаючи a (p*q) > 0, перетворимо цю задачу до такої еквівалентної форми:

(4.25)

(4.26)

(4.27)

Важливо зауважити, що перетворена задача (4.25)—(4.27) подвійна до задачі (4.16)—(4.19).

Таким чином, відшукання оптимальних стратегій обох гравців зводиться до розв'язування пари подвійних задач лінійного програмування (4.16)—(4.19) і (4.25)—(4.27). Отже, доведено таку теорему.

Теорема 4.3. Матрична одноходова гра двох гравців з нульовою сумою еквівалентна парі спряжених задач лінійного програмування.

Пара подвійних задач еквівалентна деякій самоспряженій задачі, яку можна записати в такому вигляді!

(4.28)

де в нашому випадку

Матриця задачі (4.34) кососиметрична

(4.29)

тобто a_ij.=-a_ji

Отже, теорему 4.3 можна подати також у вигляді такої теореми.

Теорема 4.4. Матрична одноходова гра двох гравців з нульовою сумою і платіжної матрицею А еквівалентна самоспряженій задачі лінійного програмування з кососиметричною матрицею (4.29), де

і

Зауваження. Як слідує з викладеного, для зведення матричної гри до лінійних задач виду (4.16)—(4.19);(4.25)—(4.27) необхідно, щоб ціна гри була більша за нуль. Цього завжди можна досягти, змінивши ціну гри на величину, що дорівнює модулю найменшого від'ємного елемента платіжної матриці, так щоб в ній залишались лише невід'ємні елементи.

Приклад. Розв'яжемо гру з платіжною матрицею (4.1а). Складемо задачу максимізації, змінивши ціну гри на ,

Розв'язуючи симплексним методом, маємо таблиці;

-x1

-x2

1

-x1

-u1

1

-u2

-u1

1

-u1=

0

2

x2=

0

1/2

1/2

x2=

0

1/2

1/2

-u2=

2

0



-u2=

2

0

1



x1=

1/2

0

1/2

z=

-1

-1

z=

-1

1/2

1/2

z=

1/2

1/2

1

Як випливає з останньої таблиці,

w*=1, звідки:

Справжня ціна гри