4. Теорія ігор і лінійне програмування

4.1. Основні поняття теорії матричних ігор

Теорія ігор є математичною формалізацією різних конфліктних ситуацій, суть яких полягає в тому, що кілька учасників прагнуть досягти певних суперечливих, як правило, цілей, причому ступінь цього досягнення залежить від способу дій (стратегій) учасників, кожний з яких прагне максимізувати міру досягнення поставленої мети [18].

Учасниками гри можуть бути як окремі індивідууми, так і цілі колективи (організації), а також різні явища і об'єкти природи (погода, надра тощо). З точки зору теорії оптимальних рішень іграми можуть вважатись такі явища, як азартні та спортивні ігри, різні конфліктні ситуації в сфері економіки та суспільного виробництва тощо.

Грою називається сукупність деяких певним чином впорядкованих правил, що реалізуються в діях двох чи більше осіб, які прагнуть досягти своїх цілей, виступаючи як учасники гри. Різні види ігор відрізняються своїми правилами і визначаються ними. Учасники гри називаються гравцями або партнерами. Ходом гри називається вибір (вибір, який зумовлює реалізацію цього рішення в процесі гри) гравцем одного рішення з множини допустимих рішень, визначених правилами гри. Елементи визначеної правилами гри множини допустимих рішень кожного окремого гравця називаються його чистими стратегіями. Отже, хід—це вибір гравцем однієї з своїх вислих стратегій. Однак в процесі гри гравці можуть приймати рішення стосовно певної множини своїх чистих стратегій, які при цьому можуть розглядатись як окремий випадок таких рішень — більш складних стратегій.

Одноразова і повна реалізація гравцями правил гри називається партією. Партія здійснюється за певне число ходів і зумовлює результат гри, який має вид платежу одних учасників іншим. Партії можуть повторюватись і в сукупності утворювати більш складні ігри.

Ігри можна класифікувати згідно з деякими основними ознаками. Однією з них є число гравців. Якщо всі учасники гри утворюють N груп, кожна з яких визначається спільною метою своїх членів, то така гра називається грою N осіб. Іншим важливим критерієм є число ходів у партії. Якщо число ходів скінчене, то така гра називається скінченою грою. В іншому разі гра буде нескінченною.

Гра може належати до певного класу в залежності від того, яка суть результату гри. Як правило, результат гри N осіб описується деякою функцією стратегії учасників гри, тобто R (s⁽¹⁾,s'²',...,s^(N)), де R—кількісний вираз результату гри, а s⁽¹⁾,s'²',...,s^(N)—стратегії гравців, що належать множинам їх допустимих стратегій Значення результату гри при оптимальних стратегіях всіх гравців називається ціною гри. Якщо R є платежем одних гравців іншим, то такі ігри називаються антагоністичними. В капіталістичній економіці відповідні задачі описують ситуації конкурентної боротьби, боротьби за максимальні прибутки. В соціалістичній економіці задачі теорії ігор можуть описувати процеси соціалістичного змагання, спеціалізації та кооперування виробництва і т.п. з метою загального підвищення ефективності суспільного виробництва. Подібні ситуації описуються класом коаліційних ігор.

Якщо сума платежів всіх учасників гри дорівнює нулю, тобто виграші одних дорівнюють програшам інших, то така гра називається грою з нульовою сумою. Якщо кожен гравець має всю інформацію про попередні ходи, то така гра називається грою з повною інформацією. Всяка інша гра є грою з неповною інформацією. Існують і деякі інші критерії класифікації ігор.

Метою теорії ігор є розробка способів відшукання оптимальних стратегій, які оптимізують результати гри. Сукупність оптимальних стратегій всіх гравців називається розв'язкою гри.

п.1. Розглянемо далі найпростіший клас ігор — одноходові матричні ігри двох гравців з нульовою сумою. Це ігри, які мають дискретну платіжну функцію R(і,j)=а_ij означену на дискретній множині чистих стратегій двох гравців: j=1;п. Якщо гравці мають т та п чистих стратегій відповідно, то елементи а_ij утворюють прямокутну матрицю розміру , що і дало назву матричним іграм. Пояснимо це більш детально.

При виборі першим гравцем і-ї чистої стратегії , а другим j-ї чистої стратегії результат гри визначається числом а_ij, яке означає виграш першого гравця і програш другого, так що сума виграшів обох гравців дорівнює нулю:a_ij-а_ij=0. Легко бачити, що при всіх можливих комбінаціях чистих стратегій першого і другого гравців величини а»у утворюють прямокутну матрицю розміром , якщо номерами чистих стратегій першого гравця позначити рядки матриці, а номерами чистих стратегій другого гравця — її колонки.

i	j
	1	…	j	…	n	. (4.1)
1	a11	…	a1j	…	a1n
…	…	…	…	…	…
i	ai1	…	aij	…	ain
…	…	…	…	…	…
m	am1	…	amj	…	amn

Означена матриця називається платіжною, або матрицею виграшів першого гравця.

Важливо підкреслити, що платіжна матриця вважається наперед відомою обом гравцям, а свої ходи гравці роблять незалежно один від одного, не маючи ніякої інформації про те, який хід вибирає партнер.

Зрозуміло, що величини а_ij, можуть бути додатними (коли перший гравець реально виграє), від'ємними (коли перший гравець реально програє) і нульовими (нічия). Наведемо для ілюстрації приклад.

Гра у відгадування. Відомий спосіб розв'язування суперечок: один партнер потай від іншого затискує в руці невеликий предмет, наприклад сірник, а другий відгадує — в правій чи лівій руці цей предмет затиснутий. Відгадування означає виграш другого і програш першого, не відгадування — зворотний результат. Отже, кожний гравець має дві чисті стратегії: перший — покласти предмет у ліву (одна чиста стратегія) або в праву руку (друга чиста стратегія); другий — показати на ліву руку партнера (одна чиста стратегія) або на праву (друга чиста стратегія). Платіжна матриця має такий вигляд:

і	j
	1	2	(4.1a)
1	—1	1
2	1	—1

п.2. Розглянемо знову платіжну матрицю (4.1). Нехай перший гравець вибирає свою i-ту чисту стратегію. Тоді оптимальною поведінкою другого гравця буде вибір тієї і-ї чистої стратегії, якій в i-му рядку відповідає мінімальний елемент матриці (тобто найменший виграш першого гравця): Так само якщо першому гравцеві відома деяка j-та чиста стратегія другого гравця, то він вибере ту i-ту свою чисту стратегію, якій відповідає максимальний елемент j-ї колонки, тобто Однак в першому випадку поведінка першого гравця буде оптимальною тоді, коли він вибере таку і-ту чисту стратегію, для якої величина а*_i буде максимальною, тобто Так само і в другому випадку: другий гравець гратиме оптимально, якщо вибрана ним /о стратегія забезпечуватиме йому мінімальний програш, тобто

Величина називається максимальним гарантованим виграшем першого гравця, а величина —мінімальним гарантованим програшем другого гравця. Якщо то, очевидно, гра має розв'язок в чистих стратегіях, тобто i₀=і*;j₀=j* являються оптимальними чистими стратегіями гравців. Елемент називається сідловин елементом платіжної матриці і являється ціною гри. Отже, пара чистих стратегій (i*;j*)=(i₀;j₀), що відповідає сідловому елементу платіжної матриці і буде розв'язком гри (сідловою точкою матриці).

Приклад. Визначити сідловий елемент такої матриці. Тут маємо:

Однак не всяка матриця має сідловий елемент. Наприклад, матриця (4.1а) сідлового елементу не має.

В загальному ж випадку справджується така теорема.

Теорема 4.1. Для довільної матриці

Доведення. Справді, згідно з означенням максимуму, для довільного j маємо , звідки випливає нерівність яка буде справедливою для будь-якого значення і в лівій частині нерівності, в тому числі і для деякого i₀ для якого

що й треба довести.

Величина зветься нижнім значенням, (нижньою ціною) гри, а величина —верхнім, значенням (верхньою ціною) гри. Стратегію i₀, що відповідає нижній ціні гри, називають максимінною, а стратегію j₀, яка відповідає верхній ціні гри—мінімаксною. Наступна теорема дає необхідні та достатні умови існування сідлової точки матриці.

Теорема 4.2. Для існування сідлового елемента матриці необхідно і досить, щоб матриця мала такий рядок і₀ і таку колонку j₀, для яких

(4.2)

Необхідність. Нехай сідловий елемент існує, тобто Очевидно, що звідки і дістаємо нерівність (4.2).

Достатність. Нехай існують такі i₀ та j₀, що виконується нерівність (4.2) для довільних і та j. Тоді

Оскільки в теоремі було показано, що для всякої матриці має місце протилежна нерівність, то

що й треба було довести.

Якщо платіжна матриця не має сідлового елемента, то і застосування гравцями стратегій, що відповідають цим числам, забезпечує (тобто гарантує) виграш не більший к і програш, не менший Р. Наприклад, нехай гра має таку платіжну матрицю:

і	j
	1		2
1	4	1		1
2	2	3		2
	4	3

Максимінною стратегією 1-го гравця буде друга стратегія (i₀=2), а мінімаксною стратегією 1-го гравця—теж друга (j₀=2). Застосування 1-м гравцем його другої стратегії гарантує йому виграш не більший 2, оскільки 2-й гравець може вибрати одну свою 1-шу стратегію, хоч при j₀=2 він реально виграє 3 одиниці; так само застосування 2-м гравцем своєї мінімаксної стратегії (j₀=2) гарантує йому програш не менший 3 і саме стільки він програє, якщо 1-й гравець застосовує свою другу стратегію.

Таке положення змушує обох гравців з метою збільшення виграшу першим та зменшення програшу другим рандомізувати вибір своїх чистих стратегій, тобто зробити цей вибір випадковим, покладаючись в певній мірі на випадок, на «везіння» в грі. В цій ситуації виникає потреба оцінити з точки зору випадкового вибору свою сукупність чистих стратегій. Такими оцінками можуть бути ймовірності застосування гравцем своїх окремих чистих стратегій. Рішення по оцінці ймовірностей вибору гравцем його чистих стратегій називають змішаною стратегією цього гравця. Отже, приходимо до такого означення.

Означення. Вектор, компонентами якого є ймовірності вибору чистих стратегій одного з гравців, називається змішаною стратегією цього гравця.

Позначимо окрему змішану стратегію першого гравця р=(p₁,p₂,…,p_m), а всю множину можливих змішаних стратегій Р={p};для другого гравця, відповідно, q=(q₁,q₂,…,q_n) і Q={q}.

Для одноходової гри очевидні рівності:

p₁+p₂+…+p_m=1; q₁+q₂+…+q_n=1, (4.3)

оскільки чисті стратегії кожного гравця утворюють повну систему елементарних подій.

Важливо надалі зазначити, що кожну чисту стратегію можна вважати окремим випадком змішаної, приписавши в останній одній імовірності, яка відповідає певній чистій стратегії, значення одиниці, а всім іншим ймовірностям, посилаючись на (4.3), нульові значення. Позначимо чисту стратегію, розглядувану як випадок змішаної, символами:

(4.4)

Розглянемо тепер випадкову подію, яка полягає в сумісному виборі першим гравцем i-ї чистої стратегії, а другим j-ї, позначивши цю подію символами (ij).

Знаючи змішані стратегії, які застосовуються гравцями, легко обчислити ймовірність події (ij), застосувавши теорему множення ймовірностей незалежних подій:

Оскільки кожній складній події (ij) однозначно відповідає елемент а„ платіжної матриці, то ймовірність (4.3) є також ймовірністю випадкового результату гри а_ij (і=1,2,...,т; j=1,2,...,п). Оскільки сукупність усіх подій (ij} становить повну систему подій, то легко обчислити математичне сподівання величини виграшу першого гравця при відомих змішаних стратегіях гравців:

(4.5)

Цілком зрозуміло, що при довільній, у тому числі й найкращій, змішаній стратегії другого гравця q перший гравець прагнутиме вибрати таку свою змішану стратегію р*, щоб математичне сподівання його виграшу було якнайбільшим, тобто

(4.6)

У його партнера прагнення цілком протилежне: при довільній змішаній стратегії першого гравця р другий гравець прагне застосувати таку змішану стратегію q*, щоб мінімізувати свій програш. Отже,

(4.7)

Зрозуміло, що стратегія р* є оптимальною для першого гравця. Це стосується і стратегії q* для другого гравця.

Припустимо, що обидва гравці застосовують свої оптимальні змішані стратегії р* і q*.

Тоді значення математичного сподівання виграшу при цьому

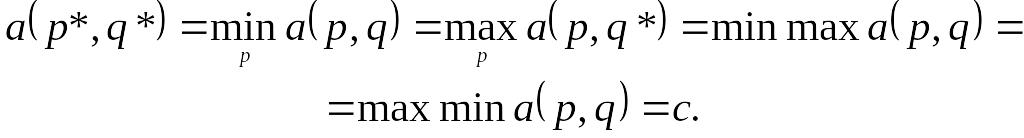` (4.8)

Вирази (4.8) випливають з прийнятої умови р=р*, q=q* і виразів (4.6), (4.7) (Обов'язкове виконання рівностен (4.8) для всякої одноходової матричної гри двох партнерів з нульовою сумою строго доводиться основною теоремою теорії матричних ігор в § 3 цього розділу (теорема Неимана).). Величина

(4.8a)

називається значенням, або ціною, гри, а оптимальні змішані стратегії р* і q*—розв'язком матричної гри.

п.3. Розглянемо задачі, розмір платіжної матриці яких дорівнює , де :

Позначимо ймовірність вибору першим гравцем першої чистої стратегії p₁=р. Тоді, очевидно, p₂=1-р. При деякій j-й чистій стратегії другого гравця математичне сподівання виграшу першого гравця буде лінійною функцією однієї змінної р, а саме:

а^(j)=а(р,q^(j))=a_1jp+a_2j(1-р)=(a_1j-a_2j)р+а_2j,.

Зобразивши всі залежності а^(j)=а(р,q^(j)), j=1,2,...,п на графіку (рис. 4.1, де п=4), легко встановити оптимальні чисті стратегії другого гравця для різних значень величини р. Справді, це будуть ті стратегії, які даватимуть найменше значення сподіванню виграшу при даному значенні р. Відрізки відповідних прямих на графіку утворюють ламану—нижню «обгортку» сімейства всіх прямих графіка (АВСД на рис. 4.1).

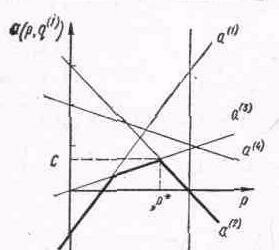
Рис. 4.1

Очевидно, що перший гравець при цьому гратиме оптимально, якщо вибере таке значення р=р*, яке відповідатиме найвищій точці (вершині) цієї ламаної (точка С на рис.27), тобто найбільшому значенню сподіваного виграшу при оптимальній поведінці свого партнера. Таким чином, з графіка легко визначити величини

p*₁=p*; p*₂=1-p*; с=а(р*,q^(j₁⁾)=a(p*,q^(j₂⁾), (4.8б)

де j₁ та j₂—номери чистих стратегій другого гравця, перетин графіків яких дає шукану найвищу вершину ламаної.

Отже, оптимальному вибору р* першого гравця відповідає лише дві можливі чисті стратегії другого гравця j₁ та j₂, а решта його чистих стратегій не реалізується, тобто

(4.8b)

якщо

Таким чином, викреслюючи всі колонки платіжної матриці, крім j₁-ї та j₂-ї одержуємо гру з матрицею і оптимальні значення та можна одержати аналогічно тому, як визначалось р*.

Дійсно, при виборі першим гравцем деякої чистої стратегії ціна гри дорівнюватиме

(4.8г)

Використовуючи вже знайдене значення ціни гри с та два довільні рівняння з системи (4.8в), (4.8г), знаходимо значення та . Третє рівняння можна використати для перевірки.

Зауваження 1. Встановивши з графіка номери можливих чистих стратегій другого гравця j₁ та j₂, що відповідають оптимальному значенню р*, числові значення р* та с можна знайти, розв'язуючи систему рівнянь (4.86).Визначаючи q*, можна в системі рівнянь (4.8в), (4.8г) вважати знову ціну гри невідомою, а для контролю обчислень співставити її значення, одержані з системи (4.86) та з системи (4.8в), (4.8г).

Зауваження 2. Зрозуміло, що для гри з платіжною матрицею , де , хід розв'язування аналогічний описаному, але спочатку слід визначити та ,а потім відповідні значення р*.

Приклад. Розв'яжемо гру з такою платіжною матрицею:

Складемо рівняння прямих для окремих чистих стратегій другого гравця:

(4.8д)

і побудуємо їх на графіку (рис.27). Точка С=(с;р*), яка є найвищою точкою ламаної АВСД, одержується в перетині прямих, що відповідають другій та третій чистим стратегіям другого гравця. Отже, перша та четверта чисті стратегії другого гравця не реалізуються при опти^ мальному виборі р=р* і їх можна відкинути, викресливши відповідні колонки платіжної матриці. Координати точки С=(с;р*) знайдемо або з графіка, або аналітичне, розв'язуючи 2-ге та 3-тє рівняння системи (4.8д), де слід покласти a⁽²⁾=а⁽³⁾=с.Маємо Складемо рівняння, аналогічні системі (4.8д), для другої та третьої чистих стратегій другого гравця:

звідки

Остаточне розв'язування задачі запишеться:

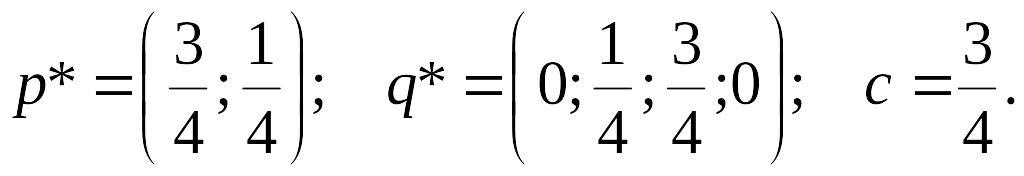
Розглянутий приклад показує, що чисті стратегії другого гравця розрізняються по можливостях їх використання у грі. Так, четверта стратегія абсолютно недоцільна при будь-якому значенні р. Назвемо такі стратегії некорисними (неактивними або зайвими). Серед, корисних (активних) стратегій другого гравця виділяються дві стратегії (друга та третя), які використовуються при оптимальній поведінці першого гравця, що визначається значенням р*. Назвемо ці стратегії ефективними. Як видно з прикладу, неефективні чисті стратегії входять в оптимальну змішану стратегію q* з рівними нулями ймовірностями, оскільки вони викреслювались при визначенні q*, в результаті чого фактично замість гри з матрицею розміру розв'язувалась гра з матрицею розміру . Отже, відбулося спрощення гри.

п.4. Розглянемо ознаки неефективності чистих стратегій в загальному випадку. Якщо для всіх координат двох довільних векторів п-вимірного простору а та b справджується нерівність а, то говорять, що вектор b домінує над вектором а, а вектор а домінується вектором b. Можна довести, що неефективним чистим стратегіям першого гравця відповідають ті рядки платіжної матриці, які домінуються деякою опуклою лінійною комбінацією всіх інших рядків цієї матриці, а неефективним чистим стратегіям другого гравця відповідають ті колонки платіжної матриці, які домінують деяку опуклу комбінацію всіх інших колонок цієї маїтиці. Якщо домінування строге, то відповідні неефективні стратегії вхі дять з нульовою ймовірністю в будь-яку оптимальну змішану стра'.егію свого гравця; при нестрогому домінуванні серед оптимальних зміц іних стратегій гравців обов'язково знайдеться така, в якій ймовірності його неефективних чистих стратегій дорівнюватимуть нулю. Отже, встановивши один з двох описаних фактів домінування, відповідні чисті стратегії гравців можна відкинути, викресливши з матриці їх колонки та рядки і поклавши рівними нулю відповідні ймовірності. Таким чином в деяких випадках вдається спростити гру, особливо якщо факт домінування очевидний.

п.5. Іноді платіжну матрицю можна розбити на блоки, кожен з яких має постійні суми елементів в кожному своєму рядку і колонці, наприклад,

Такі матриці називаються блочно-сталими. Замінивши блоки числами, що дорівнюють середнім арифметичним всіх елементів відповідного блоку, одержимо нову матрицю

Можна показати, що ціна гри з платіжною матрицею А' дорівнює ціні вихідної гри з платіжною матрицею А, а ймовірності окремих чистих стратегій вихідної гри в другій оптимальній змішаній стратегії одержуються за формулами:

де і —компоненти оптимальних змішаних стратегій спрощеної гри з платіжною матрицею А', ; —компоненти оптимальних змішаних стратегій вихідної гри, які відповідають s_i-k_i, рядкам та s_j-k_j колонкам (і;j)-го блоку. Як видно з наведених формул, ці ймовірності однакові для всіх рядків (та всіх колонок) даного блоку. Оскільки матриця А' в нашому прикладі має сідловий елемент, то а оптимальні змішані стратегії вихідної гри

Легко бачити, що ціна гри в обох випадках однакова с'=с=2.