Модель оптимізації структури машинно-тракторного парку

Необхідно визначити оптимальне використання наявних машин на сільськогосподарському підприємстві та потребу в додатковій техніці для виконання всього комплексу технологічних операцій у встановлені агротехнічні строки з мінімальними затратами.

Введемо позначення;

i – вид роботи;

m – число всіх видів робіт;

j – види машин;

n – число всіх видів машин, які є на підприємстві;

k – номер комплексу робіт;

N – число всіх комплексів робіт;

r – вид додаткових машин;

R – число всіх видів нових залучених машин;

a_ijk – змінна продуктивність j-ї машини на i-й роботі k-го комплексу;

A_ik – об’єм i-ї роботи в k-му комплексі;

Q_j – число машин j-го типу, які змінюються;

p_rk – число машин r-го типу, які можна додатково залучити для виконання k-го комплексу робіт;

q_jk – число машин j-го типу, що вибули при виконанні k-го комплексу робіт;

c_ijk – прямі експлуатаційні затрати при виконанні i-ї роботи k-го комплексу j-м видом машини даного підприємства;

t_k – тривалість k-го комплексу робіт;

b_ik – коефіцієнт змінності виконання i-ї роботи k-го комплексу;

s_ijk – затрати при виконанні робіт i-го виду k-го комплексу машинами j-го типу, які залучаються додатково;

x_ijk – число машин j-го типу, які потрібно використати для i-ї роботи k-го комплексу;

y_irk – число машин r-го типу. які необхідно придбати для виконання i-ї роботи k-го комплексу робіт.

Математична модель. Знайти мінімум затрат

при обмеженнях: на виконання агротехнічних строків

на можливості наявного парку машин

на залучені машини

на невід’ємність змінних

Розв’язуючи цю задачу, як задачу лінійного програмування, визначаємо структуру парку машин, який використовується, та число залучених машин r-го типу

Модель складення оптимальних схем внесення добрив

Необхідно отримати оптимальну схему внесення мінеральних добрив різного виду під різні культури на наявній площі.

Введемо позначення:

j – вид культури;

l – число всіх видів культур;

i – вид суміші добрив;

n – число всіх видів сумішей;

q – спосіб внесення добрив;

Q – число всіх способів внесення добрив;

r – номер форми, в якій знаходиться діюча речовина в добриві (легко- та важкорозчинні);

h – вид органічного добрива;

B – число всіх видів органічних добрив;

N_r, P_r, K_r – кількість діючої речовини азоту, фосфору та калію r-ї форми, наявного на підприємстві;

A – кількість органічних добрив, що є на підприємстві;

H_h – кількість h-го виду добрива, що є на підприємстві;

N_ijqr, P_ijqr, K_ijqr – кількість діючої речовини азоту, фосфору та калію r-ї форми, внесені по q-му способу в i-у суміш під j-у культуру на 1 га землі;

H_ijqh – кількість органічного добрива h-го виду, внесених по q-му способу в i-у суміш під j-ту культуру на 1 га землі;

H_ijq – кількість органічного добрива, що входить в i-у суміш та використовуєме q-м способом під j-у культуру;

S_iq –площа посіву під j-у культуру. в яку можна внести добрива по q-му способу;

a_ijq – логічний коефіцієнт, рівний 1, якщо можна внести i-у суміш q-м способом під j-у культуру і рівний 0 в противному випадку;

C_ijq – ефективність (прибуток), отримуєма при внесенні i-ї суміші q-м способом під j-у культуру на 1 га землі ;

x_ijq –число гектарів землі, відведене під j-у культуру з внесенням i-ї суміші добрив q-м способом.

Математична модель. Знайти максимум прибутку

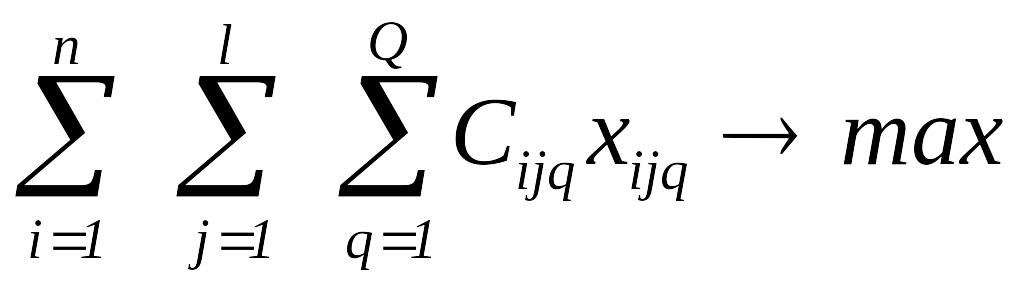
при обмеженнях на азотні добрива

на фосфорні добрива

на калійні добрива

,

на органічні добрива

на наявній площі

на невід’ємність змінних

Це задача лінійного програмування.