Модель оптимізації виробництва кормів

Деякі сільськогосподарські підприємства можуть спеціалізуватись на виробництві кормів. При цьому вирощені зернові культури частково використовуються на корма, а інша частина – як зерно. Тому спеціалізація сільськогосподарського підприємства повинна враховувати оптимальне поєднання виробництва кормів та сільськогосподарської продукції. Оптимізація звичайно проводиться по критерію мінімуму собівартості виробництва або максимуму прибутку.

Для створення моделі оптимізації виробництва кормів введемо позначення:

h – вид кормів;

j – вид сільськогосподарської культури;

r – вид сільськогосподарської продукції;

H – число видів кормів;

l – число видів сільськогосподарських культур;

R – число видів сільськогосподарської продукції;

a_jh – норма виходу h-го виду корму з одиниці j-ї культури;

b_jr – норма виходу r-го виду сільськогосподарської продукції з одиниці j-ї культури;

a_h – плановий об’єм виробництва h-го виду корму;

b_r – плановий об’єм виробництва r-го виду продукту;

c_j – собівартість виробництва одиниці j-го виду культури;

x_j – обсяг виробництва j-го виду культури, що шукається.

Модель оптимізації виробництва кормів заключається в знаходженні таких , при яких досягається мінімум собівартості

та виконуються обмеження: по плану випуску кормів

по плану випуску продукції

Таким чином, модель сформована в вигляді задачі лінійного програмування. В результаті її розв’язання отримаємо оптимальні об’єми виробництва сільськогосподарських культур, що йдуть на корм і продукцію.

Приклад 3.

Господарство може вирощувати три види сільськогосподарських культур собівартість 240, 120, 300 грн/т, з яких виробляють дві групи кормів . Показники виробництва кормів та продукції наведені в табл. 3.

Таблиця 3.

Показники виробництва кормів та продукції

Показники	Вид	Норма виходу кормів і продукції з таких культур			План по випуску кормів та продукції
		1	2	3
Корм	1 2	8 4	0 1	1 3	8 5
Продукція	1 2	2 1	5 3	0 6	6 4

Позначимо x_j – об’єм виробництва j-ї культури в тис. т. Тоді модель оптимізації виробництва кормів запишемо у вигляді: знайти x_j0 , при яких досягається мінімальна собівартість

та враховуються обмеження по виконанню плану виробництва кормів та виробництва продукції Розв’язком цієї задачі є x₁=1 тис. т., x₂=1 тис. т., x₃=0. Собівартість С=360 тис. грн.

Таким чином, точки зору мінімізації затрат найбільш вигідно вирощувати 1-й та 2-й види сільськогосподарських культур по 1 тис. т, а 3-й вид культури вирощувати не рентабельно. При цьому мінімальні затрати складуть 360 тис. грн., буде виконаний план по виробництву кормів 2-го виду продукції, а по виробництву 1-го виду продукції – перевиконаний на 1 тис. т.

Модель розміщення і структури посівів

Основними ресурсами сільськогосподарського підприємства є земельні наділи. Урожайність а значить і рівень рентабельності господарства залежить від видів наділів землі, що виділені під сільськогосподарські культури. Тому з метою підвищення ефективності виробництва сільськогосподарських культур слід провести найкраще розподілення земельних угідь під культури, які вирощуються.

Для створення моделі введемо позначення:

i – номер наділу землі;

n – число всіх наділів землі;

j – вид сільськогосподарської культури;

l – число всіх видів культур;

b_i – площа i-го наділу землі, га;

a_j – площа, що відводиться під j-ту культуру, га;

c_ij – собівартість обробки одиниці площі i-го наділу під j-ту культуру;

x_ij – площа, відведена на i-му наділу під вирощення j-ї культури, га.

В цій моделі обробітку та структури посівів потрібно знайти такі при яких достягається мінімум затрат

дотримується баланс площ

та виконуються обмеження: по величині наділів землі

по розміру площі , відведеної для вирощування культури,

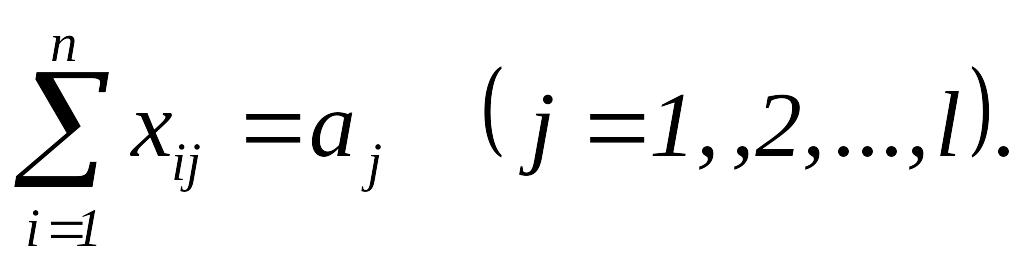
Модель представляє собою транспортну задачу, для розв’язання якої існують ефективні методи. Вона спрощена тим, що не враховується врожайність культур. Якщо прийняти до уваги цей фактор, то слід ввести додаткові позначення: a_ij – урожайність j-ї культури.

Тоді модель буде мати вигляд

при умові виконання плану по виробництву культур

та використання наявних площ

В такому випадку модель являє собою розподільну задачу.

Приклад 4.

В господарстві є два наділи землі , дорівнюють b₁=10 тис. га, b₂=15 тис. га. На цих наділах потрібно вирощувати два види сільськогосподарських культур: перший – зерно, другий – цукровий буряк. Техніко-економічні показники виробництва продукції наведені в таблиці 4.

Необхідно визначити x_ij- площа i-го наділу, що відводиться під j-ту культуру. Тоді модель має вигляд

Таблиця 4.

Техніко-економічні показники виробництва

Продукція	1-й наділ		2-й наділ		План виробництва, тис. ц
	Врожайність, ц\га	Собівартість руб./ц	Врожайність, ц\Га	Собівартість руб./ц
Зерно	20	4,0	25	2,5	500
Цукровий буряк	200	2,5	250	2,1	400

при умовах: використання наявних площ земельних наділів , виконання плану виробництва культур та реальності умов

Розв’язком цієї задачі являється тис. га, тис. га, , тис. га, С=2447500 грн.

У відповідності з оптимальним планом для виробництва зерна потрібно відвести 10 тис. га 1-го наділу і 13,4 тис. га 2-го наділу землі, а для цукрового буряка – 1.6 тис. га 2-го наділу землі. Тоді будуть використані всі наявні площі, вироблено зерна тис. ц, цукрового буряка тис. ц і мінімальні затрати складуть 2447500 грн.