3.1. Лінійні економіко-математичні моделі в сільськогосподарському виробництві

В економіко-математичних моделях сільськогосподарських підприємств необхідно враховувати, що земля як основний засіб виробництва сільського господарства є універсальною по виробництву продукції; сільськогосподарський труд менше спеціалізований та створює великі можливості зміни праці; в сільськогосподарському виробництві є велика різноманітність природнокліматичних умов, які визначають відносно стійку диференціацію продуктивності праці в різних районах; для сільського господарства характерна взаємозамінність виробленої продукції; сільськогосподарське підприємство є основною ланкою, яка виробляє сільськогосподарську продукцію.

Економіко-математичні моделі та методи допомагають розв’язувати багато задач планування та управління сільськогосподарським виробництвом.

Базова модель оптимального поєднання галузей

Задача оптимального поєднання галузей сільського господарства полягає в визначенні оптимального направлення розвитку сільськогосподарського підприємства по структурі виробництва та використанню ресурсів. В якості критерію ефективності використовується максимум прибутку.

Введемо позначення:

j – номер виду сільськогосподарської продукції;

L – число видів сільськогосподарської продукції;

l – число видів продукції землеробства;

j = 1, 2, …, l – вид продукції землеробства;

j = l + 1, l + 2, …, L – вид продукції тваринництва;

s – номер виду виробничого ресурсу;

m – число видів виробничих ресурсів;

b_s – об’єм s-го виду ресурсів, який надається зовні для виробництва продукції;

p_j – прибуток, отриманий сільськогосподарським підприємством від реалізації одиниці j-го виду продукції;

x_j – об’єм виробництва j-го виду продукції, a_sj – норма затрат s-виду ресурсу на виробництво одиниці j-го виду продукції;

h – номер групи кормів;

H – число всіх груп кормів;

i – номер виду елемента живлення;

a_ijh – норма затрат i – го елемента живлення по h–й групі кормів на виробництво одиниці i-го виду продукції тваринництва;

a_ijh - зміст i –го елементу живлення в одиниці j –го виду культури землеробства, що використовується на корм по h-й групі кормів;

q_j - масова частка j-ї культури, що використовується на корм;

b_ih – число кормових ресурсів (елементів живлення i–го виду), що входять в h-у групу кормів, що поступили зовні на сільськогосподарські підприємства.

Математична модель. Знайти такі об’єми виробництва x_j (j = 1, 2, …, L) сільськогосподарської продукції, при яких досягається максимум прибутку.

та виконуються умови виробництва по виділеним зовні ресурсам

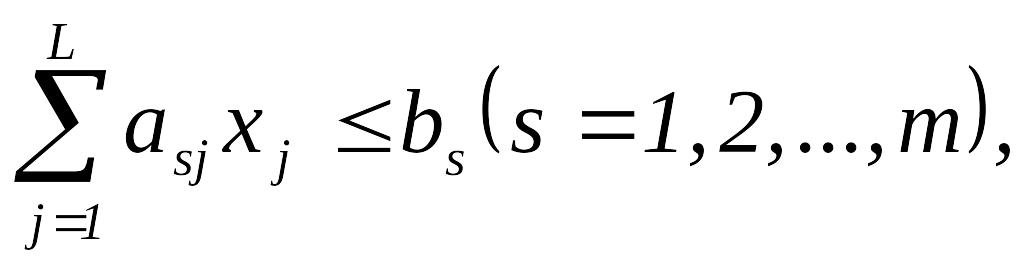
по додатковим кормам, що виробляються в даному господарстві,

при невід’ємних змінних . Отримана модель в вигляді задачі лінійного програмування, для розв’язання якої можна примінити симплекс метод та отримати структуру виробництва продукції з використанням ресурсів на сільськогосподарському підприємстві.

Приклад 1.

В господарстві вирощується зерно, кукурудза на силос та утримується велика рогата худоба. Для вирощування сільськогосподарських культур виділяється 10 тис га пашні, для утримання худоби – 1 тис. га природних пасовищ, для виробництва всіх робіт – 200 тис. людино-днів трудових ресурсів. На утримання однієї корови затрачується 25 людино-днів праці і 40 кормових одиниць, при цьому прибуток 460 грн. на рік. З одного га природних пасовищ можна отримати 5 ц кормів. Окрім того, на корм відводиться весь урожай кукурудзи на силос і 20% валового збору зерна. Інші показники виробництва наведені в таблиці 1. Прямого прибутку від виробництва кукурудзи на силос господарство не має, вона отримується за рахунок використання кукурудзи в якості корма для худоби. Потрібно знайти оптимальне поєднання виробництва продукції. Позначимо: x₁ – об’єм виробництва зерна в центнерах, x₂ – об’єм виробництва кукурудзи на силос в центнерах, x₃ – число корів.

Таблиця 1.

Показники виробництва продукції землеробства

Культура	Урожайність, 1га, ц	Затрати труда на 1 га, людино-днів	Коефіцієнт переведення на кормову одиницю	Прибуток з 1 ц, грн.
Зернові	20	2	1,1	4
кукурудза на силос	400	20	0,2	-

Оскільки 20% зерна йде на корм худобі, то реалізується (1-0,2)x₁ зерна по ціні 4 грн. за ц. Прибуток від однієї корови дорівнює 460 грн. Загальний прибуток складає

В задачі враховуються обмеження по кормам 40 , по орних землях , по трудових ресурсах . Наприклад, обмеження по кормах, в центнерах, формується так: постійна частина від 5000 ц отримується за рахунок природних пасовищ; - за рахунок 20% зерна, виділеного на корм худобі; 0,2 x₂ – корма за рахунок кукурудзи на силос. Використання кормів – 40 x₃ – для худоби.

Для обмежень по пашні використовуються показники врожайності: для отримання 1 ц зерна потрібно 1/20 га пашні, для отримання 1 ц кукурудзи 1/400 га.

Для обмежень по трудових ресурсах використовуються трудовитрати на отримання 1 ц зерна 21/20 людино-днів, на отримання 1 ц кукурудзи на силос 1/40020 людино-днів, на утримання 1 корови – 25 людино-днів.

Розв´язавши дану задачу, отримаємо: x₁ =154214,6 ц, x₂=915708 ц, x₃=5552 корів, p=3047280 грн.