Стохастична задача спеціалізації с.-г. Виробництва

При побудові економіко-математичних моделей для сільськогосподарських підприємств приходиться враховувати наступні фактори: явно виражену сезонність у землеробстві, що робить визначений вплив на тваринництво; розбіжність робочого періоду виробництва сільськогосподарської продукції з загальним періодом виробництва; визначена залежність результатів сільськогосподарського виробництва від погодних умов, тобто показники сільськогосподарського виробництва в значній мірі залежать від його спеціалізації.

Найважливішою вимогою спеціалізації сільськогосподарського виробництва є забезпечення його комплексного розвитку на основі суспільного поділу праці, найбільш повного й ефективного використання землі й інших виробничих ресурсів, обліку природнокліматичних і економічних умов кожного району і сільськогосподарського підприємства.

Актуальність рішення даної задачі порозумівається тим, що норма витрат ресурсів на виробництво одиниці тих самих продуктів у різних господарствах не однакова, а визначається об'єктивними (природними і погодними умовами, родючістю ґрунтів і іншими) і організаційними факторами. Істотний вплив на рішення цієї задачі роблять державні закупівлі сільськогосподарської продукції. Багато в чому структуру виробництва колгоспів і радгоспів визначають державні заготівлі, що складають близько 90 % усієї товарної продукції і, що впливають на розвиток сільськогосподарського виробництва.

Сільськогосподарське підприємство — багатогалузеве господарство, його ефективність знаходиться в залежності від сполучення галузей.

При постановці задачі приймаються такі передумови:

підприємство повинне розвиватися з обліком наявних земельних, трудових і матеріально-грошових ресурсів;

обсяг виробництва основних видів продукції повинний забезпечувати виконання державного плану, задоволення внутрішньогосподарських потреб і розширене відтворення;

розміри галузей можуть бути обмежені, наприклад, у рослинництві вимогами сівозміни, у тваринництві — наявністю місць для худоби і природними темпами приросту череди.

Для комплексних підприємств варто враховувати також, що обсяг виробництва кормів планованого року повинний погоджуватися з перехідним запасом минулого року і потребою в наступному році (до нового врожаю), а також погоджувати розмір тваринницьких галузей з обсягом кормовиробництва. При цьому для кожного виду тварин необхідно визначити оптимальний раціон годівлі.

Як критерій оцінки ефективності сільськогосподарські-підприємства приймається максимум вартості кінцевої продукції або максимум прибутку.

Для побудови економіко-математичної моделі введемо наступні позначення: т — види ресурсів, наприклад, земельні угіддя, водні ресурси, добрива, трудові ресурси; п — кількість галузей, що розвиваються в даному господарстві; - норма витрат і-го ресурсу на одиницю j-й продукції; - обсяг ресурсів і-го виду; - ціна одиниці j-го продукту; i = 1, 2, ..., т; j = 1, 2, ..., п. Знаючи ці величини, сформулюємо задачу.

Визначити обсяги виробництва продукції j-го виду, при яких максимізується загальний обсяг виробництва у вартісному вираженні при дотриманні певних обмежень на вибір рішення.

Потрібно знайти такі =1,2, ..., п, що в області G, визначеної умовами виду

(3.1)

(3.2)

максимізують функцію

(3.3)

Тут — директивні вказівки з продажу державі продукції j-го. виду, j = 1, 2, ..., п.

Розглянута модель враховує лише одну сторону спеціалізації — визначення обсягів виробництва продукції в залежності від власних витрат.

Розглянемо задачу спеціалізації для комплексного сільськогосподарського підприємства.

Нехай відомо, що — норма витрат k-го елемента харчування по h-й групі кормів на виробництво одиниці j-й продукції тваринництва; — зміст k-го елемента харчування в одиниці l-й культури h-й групи кормів; d_l — частка l-й культури рослинництва, використовувана для відгодівлі тварин. Тоді кількість k-го елемента відгодівлі, що поступили від рослинництва,

а потреба в k-м елементі відгодівлі для тваринництва визначається величиною

де y_j — обсяг виробництва j-й галузі тваринництва, x_l — обсяг l-й галузі рослинництва, j = 1, 2, ..., s; l = 1, 2, ..., п.

Найбільш істотним фактором, що визначає рівень виробництва тваринницької продукції, є забезпеченість тварин кормами. Стабілізацію забезпеченості тварин кормами здійснюють трьома шляхами: у процесі виробництва (зрошення, доведення частки пар до оптимальних розмірів, підвищення культури землеробства); у процесі розподілу і перерозподілу кормів (створення страхових запасів, покупка); у процесі їхнього споживання (зміна структури раціону відгодівлі в припустимих межах).

Нижче приведемо модель, що дозволяє аналізувати забезпеченість тварин кормами при умовах, що змінюються. У зазначеній моделі будемо вважати, що формування кормової бази здійснюється за рахунок кормів, що надійшли і производимых у даному господарстві, а також за рахунок покупних кормів.

Нехай b_lh — покупні корми l-го виду по h-й групі кормів.

Тоді можна записати обмеження типу виробництво — споживання по кожному елементі відгодівлі

(3.4)

Економіко-математична модель спеціалізації багатогалузевого сільськогосподарського підприємства має вигляд

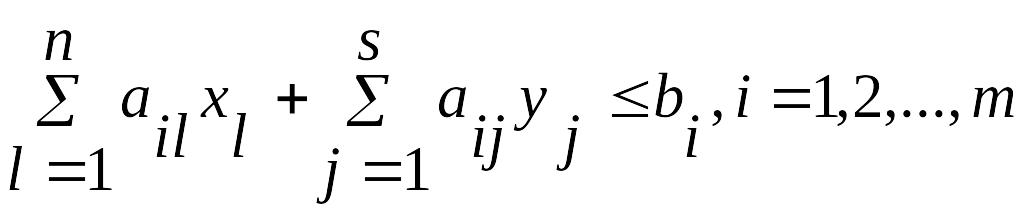(3.5)

(3.6)

(3.7)

(3.8)

Тут — частка l-й сільськогосподарської культури землеробства, що йде на власні нестатки сільськогосподарського підприємства; — частка тварин j-го виду, що йдуть на власні нестатки сільськогосподарського підприємства; - директивні завдання з продажу j-го виду тварин державі.

Потрібно знайти такі які в області G, визначеної умовами (7.5) — (7.8), максимізують прибуток сільськогосподарського підприємства, одержуваний від землеробства і тваринництва

(3.9)

де — середня ціна одиниці продукції тваринництва j-го виду, j= 1, 2,..., s.

Опишемо обмеження моделі: умова (3.5) враховує потреба і наявність ресурсів кожного виду. Слід зазначити, що якщо деякий вид ресурсів р не використовується для тваринництва, те відповідний параметр a_pj = 0, аналогічно, якщо ресурс k-го виду не використовується в землеробстві, то а_kl=0. Обмеження (7.6) враховують наявність і потреба для тваринництва в кормових культурах по видах. Обмеження (3.7) визначають співвідношення між виробництвом кожної культури землеробства, використанням її для нестатків тваринництва й інших власних потреб сільськогосподарського підприємства і директивних завдань із продажу державі відповідних культур.

Якщо деякий вид сільськогосподарської продукції виробляється лише для зовнішніх постачань і не використовується ні у тваринництві, ні в даному сільськогосподарському підприємстві, то обмеження (3.7) має вигляд

тобто необхідно робити продукції не менше директивного завдання, що визначається величиною

Обмеження (7.8) визначають співвідношення між директивними вказівками з продажу державі відповідною тварин, чередою і частиною тварин, що йдуть на власні нестатки сільськогосподарського підприємства.

Отримана економіко-математична модель з частково цілочисельними змінними лінійними обмеженнями і лінійною цільовою функцією може бути реалізована одним з методів, приведених у [х].

Для районів країни з хитливим вологовмістом ґрунту становить інтерес задача забезпеченості тварин кормами.

Відомо, що обсяг виробництва кормових культур у цих районах істотно залежить від кількості опадів, що випадають у весняно-літній час. З огляду на це, виконаємо економіко-математичне моделювання цієї задачі на основі стохастичних моделей.

Введемо наступні позначення;

j — номер виду кормів,

; i — номер елемента харчування,

, t— номер ресурсу,

— номер виду тварин,

— номер групи кормів,

— номер групи сільськогосподарських культур,

— безліч сільськогосподарських культур,

— підмножина товарних культур,

— підмножина кормових культур, що вирощуються для h-го виду тварин,

— номер культури;

v — номер результату,

v = 1, 2, ..., N; q — номер виду товарної продукції,

— підмножина видів товарної продукції тваринництва;

Q₂ — підмножина видів товарної продукції рослинництва;

— площа s-й кормової культури для h-го виду тварин у v-м результаті;

— кількість кормів j-го виду, яку варто виділити h-му виду тварин при v-м результаті;

— поголів'я h-го виду тварин у v-м результаті;

— площа s-й кормової культури для h-го виду тварин у v-м результаті, продукція якого використовується в (v+n)-м результаті;

— площа s-й кормової культури в v-м результаті, продукція якої використовується в (v+n)-м результаті;

a_ij — зміст i-го елемента харчування в j-м кормі;

— вихід j-го виду корму з одиниці площі s-й кормової культури в v-м результаті;

— витрати ресурсу t-го виду на одиницю площі s-й культури в v-м результаті;

— витрати ресурсу t-го виду на одну голову h-го виду тварин у v-м результаті;

— обсяг ресурсу t-го виду в v-м результаті;

— витрата товарної продукції рослинництва q-го виду з одиниці площі s-й товарної культури в v-м результаті;

d_hi — потреба h-го виду тварин у i-м елементі харчування;

— мінімальна і максимальна частка k-й групи кормів у раціоні h-гo виду тварин;

— частота v-го результату;

— коефіцієнт утрат при збереженні j-го виду корму;

— витрати на одиницю площі s-й кормової культури в v-м результаті;

— витрати на збереження кормів зроблених з одиниці площі s-й кормової культури в v-м результаті для результату v+n;

— витрати на виробництво j-го виду корму в v-м результаті;

— чистий прибуток від одиниці площі s-й культури в v-м результаті;

— вартість продукції за винятком усіх витрат, крім вартості кормів, одержуваних від h-го виду тварин у v-м результаті. Математичне чекання чистого прибутку визначиться

(3.10)

Запишемо умови балансу по ресурсах

(3.11)

Обсяг виробництва кінцевої продукції по галузях повинний бути не менше планового

тобто для рослинництва

(3.12)

для тваринництва

(3.13)

Для узгодження рослинництва з тваринництвом і оптимізацією відгодівлі кожного виду тварин необхідно:

балансувати раціони кожного виду тварин по елементах харчування

(3.14)

враховувати зміст окремих груп кормів у раціоні

(3.15)

Крім того, умова рівності площ по варіантам

(3.16)

умова рівності поголів'я тварин по варіантам

(7.17)

умова невід’ємності шуканих змінних

(3.18)

Отже, в області G, визначеної умовами (3.11) – (3.18), потрібно знайти

при яких максимізується функція (3.10).

Як видно з моделі, структура посівних площ не зміниться по варіантам; по варіантам змінюється напрямок використання культур.

Отримана багато етапна задача стохастичного програмування може бути вирішена одним з градієнтних методів.