Стохастичне моделювання виробництва при зрошенні.

Постановка задачі і економіко-математична модель. Сільськогосподарське виробництво в умовах зрошення має суттєві особливості, що вимагає побудови спеціальних моделей планування і економічного аналізу. Такі моделі повинні враховувати цілий комплекс природних факторів, які визначають доцільність зрошення, а також варіанти його організації, техніки і технології.

Зрошувальне землеробство слід розглядати у поєднанні з богарним (незрошувальним) як складний варіант його інтенсифікації. Тут використовується специфічний ресурс - вода для зрошування. Для її відбору з водного джерела, транспортування і подачі на поля під визначені культури в необхідній кількості і в потрібний час створюються обслуговуючі та виробничі комплекси - зрошувальні системи (ЗС). Великі інженерні ЗС мають свої виробничі ресурси, технології, організаційну структуру і управління. Продуктом функціонування ЗС є вода, що поступає на поля. Собівартість її визначається експлуатаційними затратами ЗС, які залежать від відстані та умов транспортування, від водопровідної і розподільної системи каналів, трубопроводів, лотків; від висоти підкачок; від умов зберігання води в водосховищах та ін. Ефект від зрошування в сільському господарстві визначається приростом врожайності культур і продуктивності тварин. Як правило ЗС обслуговують багато господарств з різними природноекономічними умовами виробництва. ЗС та обслуговуючі її господарства утворюють більш складну виробничу систему - зрошувальний комплекс (ЗК).

При проектуванні створення або реконструкції ЗК співставляються і оцінюють варіанти водозабору, трас поглядання і потужностей ділянок водопроводячої і розподільної мережі, ємкості водосховищ, потужностей і місць розташування насосних станцій та інших споруд ЗС, а також варіанти конкретних масивів сільськогосподарських угідь, що готуються до зрошування в господарствах. При плануванні експлуатації ЗК розглядають варіанти посівів культур на зрошувальних масивах; варіанти розподілу води між господарствами, полями, культурами; технологічні і технічні варіанти поливів; варіанти норм і режимів зрошення культур.

Економіка зрошення в вирішальному ступені залежить від природних факторів: від характеристик джерел води і ділянок зрошення, від величини і характеристик розподілу опадів. В посушливі роки витрати на зрошення можуть різко зростати, але в той же час збільшується об'єм додаткової продукції з зрошених ділянок. Ці затрати і ефект різноманітні для різних господарств, ділянок і культур, що дає підстави для пошуку оптимальних варіантів зрошення.

Кількість опадів і водності рік має ймовірну природу. Отже, додаткові затрати на зрошення і об'єми додаткової продукції від зрошення є випадковими величинами. Ці величини і визначають річний і середньорічний економічний ефект від зрошення в даних умовах. Тому для рішення планово-економічних задач зрошення необхідно застосовувати стохастичні моделі. Задачі вибору оптимальних розмірів зрошування і задачі оптимізації структури зрошуваного землеробства у поєднанні з богарним для зон рискового землеробства можуть бути вирішені лише з використанням стохастичних моделей.

При рівних умовах можливості поливу культур залежать від об'єму води в джерелі зрошування Q (м³ за зрошувальний сезон). Необхідність поливів визначається кількістю опадів  (мм за сезон). Часто ці величини коливаються по рокам в дуже невеликому діапазоні значень. В такій ситуації, коли можливість і необхідність поливів неможливо визначити наперед і отже, важко сказати про ефективність зрошення і доцільності заміни богарного землеробства зрошувальним. Це дуже ускладнює проблему вибору оптимальних параметрів розвитку зрошення. Ключовим розв'язком тут є вибір площі зрошувального масиву x (га) і сумарної потужності зрошувальної мережі N (пропускної можливості мережі за сезон в м³), так як він визначає всі інші техніко-економічні параметри проектуємої ЗС. Припустимо, що питання про вибір оптимальних розмірів зрошення розглядається для зони недостатньо зволоження, де величину  можна вважати практично стабільною. Випадковою є лише кількість води в річці Q, доступною для відбору на нужди зрошення. Відома також функція розподілу цієї величини f(Q), Q[ ]. Припустимо, що у випадку недостатку води для зрошення при незмінній середній по культурам нормі зрошення q (м³ на 1 га за сезон) скорочуються площі поливів. Тоді необхідна потужність зрошувальної мережі однозначно вибраної площі зрошення: N=qx.

Нехай вибрана площа найбільшого зрошення . Якщо вибрати площу x так, що , то буде полита не вся площа, а лише га: Оскільки питомі показники ефекту на 1 га посіву культур при поливах і без зрошування різні, то сумарний річний ефект Ф буде залежати не тільки від вибраної площі х, але й від ступені реалізації водності: Ф=Ф(x,Q). А оскільки Q випадково міняється за роками, то ефективність вибору розміру зрошення буде виражатись випадковою величиною і її можна визначити лише за результатами виробництва минулих років. Її можна виразити, наприклад, як середній річний показник ефективності (середнє по реалізації Q):

Оптимальним розміром зрошення будемо вважати таку площу масиву, який зрошується х* і відповідно потужність мережі N*=qx*, при яких величина досягає максимуму.

Моделювання процесу вибору оптимальних розмірів зрошення заключається в визначенні конкретної функції ефекту. Зрошуване землеробство є одним з варіантів технології землеробства і часто заміняє, витісняє уже існуюче богарне землеробство. Тому в моделі необхідно зрівняти ефект від вирощування культур на богарі і при зрошуванні.

В якості показника економічної ефективності землеробства візьмемо сумарний чистий дохід з загальної площі пашні S, на якій в принципі можливе зрошувальне землеробство.

Нехай в даних умовах можна вирощувати m культур, причому частина з них або всі - при зрошуванні. Якщо до зрошування підготовлюється площа x га, то площа, яка залишилась S-x залишається під богарне землеробство. Припустимо, що посіви культур організуються в сівозміни, різні для зрошуваного і богарного масиву. Співвідношення полів в зрошувальній сівозміні характеризується числами 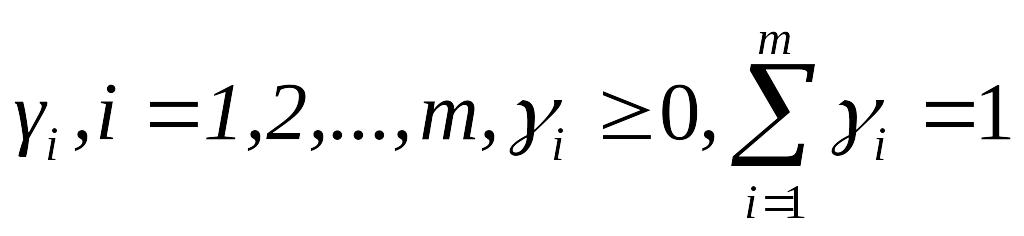, які вказують долю культур в загальній площі сівозміни. Сівозміну для богарного масиву визначимо числами Тоді x_i і - площі посівів i-культури відповідно на зрошуваному масиві і на богарі; q_i - оптимальна норма зрошення i-культури в м³ на 1 га за сезон (брутто).

При вирощуванні i-культури на богарі норматив чистого доходу дорівнює грн. на 1 га. Норматив чистого доходу на зрошуваному масиві при поливі, які забезпечують оптимальну зрошувальну норму q_i, складає грн. на 1 га з врахуванням експлуатаційних затрат в ЗС, капітальних затрат на водогосподарське будівництво і підготовку масиву до зрошення. Якщо води не вистачає, то на частині площі, підготовленої до зрошення, але не поливній в маловодний рік, отримують чистий дохід на 1 га, який враховує капітальні витрати на будівництво ЗС, розрахованої на обслуговування всього масиву x, і на підготовку його до зрошення. Звичайно, що хоча б для основного складу культур сівозмін; інакше немає сенсу розглядати питання розвитку зрошування. Окрім того, виконується умова .

Відмітимо, якщо води Q не вистачає для поливу всіх культур повними нормами, то поливати необхідно перш за все ті культури, які дають більший чистий дохід на 1 м³ використаної води, тобто у відповідності з величинами Припустимо, що всі культури впорядковані в порядку зменшення , так що Кількість води, необхідної для зрошення всієї площі посівів культур від першої до (k-1) і до k-ї включно, позначимо відповідно через , де

Припустимо, що Тоді для k-культури будуть мати місце наступні ситуації.

1) Якщо 0QQ_k, то згідно оптимальної тактики розподілу води по культурам, коли вигідніше поливати культури з меншими нормами, зрошувана площа k-культури повинна дорівнювати нулю, незрошувана x_k і богарна . Сумарний річний чистий дохід від k-культури буде дорівнювати

2) Якщо Q_kQ , то відповідні площі складуть Сумарний річний дохід дорівнює

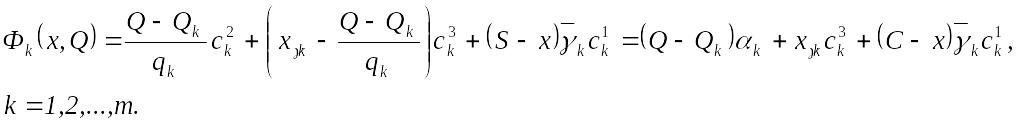
3) Якщо Q, то відповідні площі будуть дорівнювати x_k, 0 і , а сумарний річний чистий дохід від k-культури

Таким чином, якщо площа зрошення вибрана в розмірі x, а в нинішньому році величина водності ріки склала Q, то при оптимальній тактиці поливів (задоволення потреб культур у воді по черзі) сумарний чистий дохід з площі S скла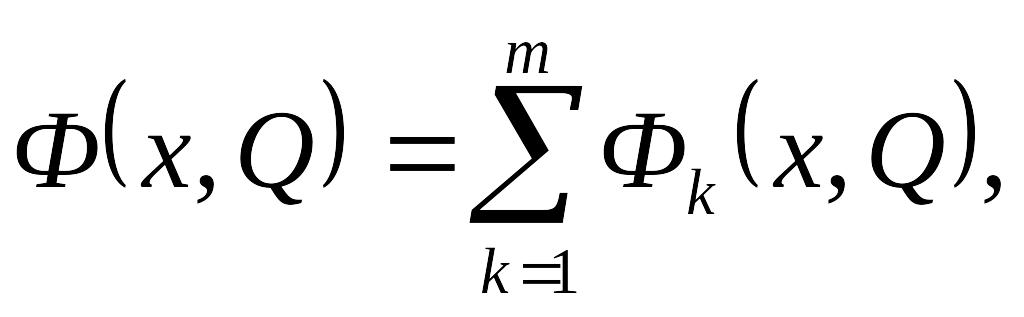де де визначені вище і залежать від того, в який напівінтервал впорядкованої множини напівінтервалів , k=1,2,…, m+1, попаде випадкова величина водності .

Задача полягає у виборі такого стратегічного рішення x*, при якій середній очікуваний по всіх реалізаціях Q чистий дохід з площі чистий дохід з площі чистий дохід з площі чистий дохід з площі чистий дохід з площі S був максимальним. Іншими словами, необхідного вирішувати задачу класичної оптимізації, тобто знайти Підставляючи конкретні вирази для Ф_k отримаємо кінцеву модель задачі.

Для знаходження х*, який максимізує функціонал , необхідно розв’язати рівняння . Очевидне виписування та спрощення цього рівняння приводить до алгебраїчного рівняння, рішення якого дозволяє знайти оптимальні параметри розмірів зрошення: х*, га, та м³ за сезон.