Алгоритм повних виключень Жордана-Гаусса для розв’язування системи лінійних рівнянь

Нагадаймо відомий з курсу лінійної алгебри алгоритм Жордана-Гаусса розв’язування системи лінійних рівнянь.

Розглянемо систему з m лінійних рівнянь, що містить n невідомих:

. . . . . . . . . . . . . . . . . . . . . . . . . .

3.10)

1-й крок. Нехай в системі (3.10) . Перетворимо перше рівняння, розділивши обидві його частини на . Маємо

(3.11)

д

(3.12)

(3.13)

е

звідки

Підставивши в решту рівнянь системи (3.10) замість x₁ вираз (3.13), одержимо

(3.14)

.

(3.15)

. . . . . . . . . . . . . . . . . . . . . . . . .

де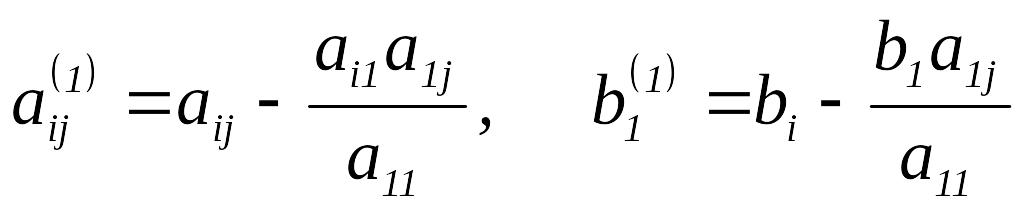

в чому легко переконатись шляхом безпосередніх обчислень.

2-й крок. Вважаючи, що перетворимо друге рівняння системи (3.10), тобто перше рівняння підсистеми (3.14), поділивши його на

(3.16)

д

(3.17)

(3.18)

е

Виключимо x₂ з усіх рівнянь системи, крім другого, в тому числі і з першого (3.11), підставляючи в них замість x₂ ліву частину рівності (3.18). Після цього система набуде вигляду

(3.19)

де

Вважаючи, що всі a_ij0 і продовжуючи алгоритм після m кроків, перетворимо систему до виду

(3.20)

де

Система (3.20) еквівалентна системі (3.10) і являється канонічною формою системи лінійних рівнянь.

З (3.20) випливає

(3.21)

Елементи , яким належить головна роль при перетвореннях системи, називаються розв’язуючими. Трапляються ще такі назви: ведучий, генеральний, головний, ключовий.

Рівності (3.21) являють собою загальний розв’язок системи (3.10). вони виражають m залежних змінних x₁, x₂, …, x_m через k=n-m незалежних змінних , які можуть набувати довільних значень. Якщо незалежним змінним надати довільних, але фіксованих значень, то (3.21) одержимо окремий (або частинний) розв’язок системи.

Базовим розв´язком системи лінійних рівнянь називається такий частинний її розв’язок, в якому всі незалежні змінні дорівнюють нулям. Покладаючи в (3.20) чи (3.21) маємо що є і базовим розв´язком системи (3.10). Слід зауважити, що в системі (3.20) колонки коефіцієнтів при залежних змінних утворюють одиничну матрицю m-го порядку, тобто відповідні вектори є базою m-вимірного векторного простору. Тому залежні змінні, яким відповідають базові вектори, називають ще базовими змінними, а незалежні – не базовими.

Для того, щоб систему (3.10) можна було перетворити до виду (3.20) необхідно, щоб в (3.10) вектори основних умов, які відповідають базовим змінним, були лінійно незалежними. Перетворення системи (3.10) до виду (3.20) рівносильне множенню (зліва) системи (3.10) на матрицю, обернену до матриці, утворюваної цими векторами. Справді, розділивши змінні на базові і небазові і матрицю основних умов задачі на дві відповідні підматриці, запишемо систему (3.10)

(3.22)

Знайшовши матрицю і помноживши на неї (ліворуч) рівняння (3.22). маємо

(3.23)

що еквівалентне системі (3.20).

Стандартна і канонічна форми задач лінійного програмування

Загальна форма задачі лінійного програмування (3.1) – (3.6) не придатна для побудови досить простих і ефективних методів розв’язування її, причиною чого є неоднорідність системи умов (3.2) – (3.6). Тому, як правило, задачу зводять до стандартної форми, в якій треба знайти максимум чи мінімум цільової функції при системі основних обмежень-рівнянь та умові невід’ємності усіх змінних:

(3.33)

(3.34)

(3.35)

Ранг сумісної системи обмежень (3.10) r можна вважати таким, що дорівнює m, оскільки в іншому разі частину, а саме: m-n=k рівнянь, треба було б відкинути, бо вони були б лінійними комбінаціями r базисних рівнянь. Отже, знайти множину планів задачі означає знайти множину невід’ємних розв´язків системи лінійних рівнянь (3.10).

Розглянемо способи переходу від загальної форми задачі лінійного програмування до стандартної.

1-й крок. До кожної лівої частини нерівностей (3.3) додамо нову невід’ємну змінну , яка дорівнює різниці між правою і лівою частинами нерівності, тобто

. (3.36)

Тоді група нерівностей (3.3) перетвориться на рівняння

Цього ж результату досягнемо, віднімаючи від кожної лівої частини нерівностей (3.4) нову невід’ємну частину , яка дорівнює різниці між лівою та правою частинами відповідної нерівності

(3.37)

отже введення m-n нових додаткових невідомих дає змогу нерівності (3.3) і (3.4) зводити до еквівалентних рівнянь, чим збільшується на m-k розмірність простору невідомих змінних. Щоб показати еквівалентність добутої системи рівнянь вихідній початковій системі нерівностей досить зауважити. що для будь-якого конкретного розв’язку системи нерівностей (3.3), (3.4) однозначно визначається і система додаткових змінних згідно формулам (3.3) і (3.4). геометричний зміст заміни видно з рис. 3. Справді, множиною розв’язків нерівності є півплощина, що містить початок координат координатної площини (x₁, x₂), а рівності при додатковій умові - півплощина АВС площини в тримірному просторі, треті координати точок якої невід’ємні.

2-й крок полягає в зведенні до однорідної системи обмежень на знак. Умови недодатності (3.3) легко перетворюються в умови невід’ємності за допомогою заміни змінних (3.8). Складніше позбутися змінних, на знак яких обмежень не накладено. Цього можна досягти двома способами.

1-й спосіб. Якщо число змінних (3.7) менше, ніж число обмежень основної групи ( тобто n-s<m) і колонки коефіцієнтів при них разом з деякими іншими утворюють базисний мінор, то, розв’язавши добуту на першому кро2і систему основних обмежень (3.150 відносно n-s згаданих змінних, виключаємо їх як з системи умов, так і з цільової функції, залишаючи без уваги формули, що виражають їх через невід’ємні змінні аж до знаходження оптимальних значень невід’ємних змінних, підставляючи які у залишені вирази, дістаємо й оптимальні значення змінних (3.7).

Хоч цей спосіб придатний для більшості практичних випадків, однак буває, що умови, необхідні для його використання, не виконуються Тоді цим способом можна виключити лише частину вільних змінних, а до тих, що залишились у задачі, застосувати 2-й спосіб, який полягає в тому, що кожну змінну, на знак якої не накладено обмежень, подають у вигляді різниці двох невід’ємних змінних

де (3.38)

Визначивши оптимальні значення та , можемо знайти за (3.38) і оптимальне значення відповідних .

Приклад. Звести до стандартної форми таку задачу лінійного програмування:

Введенням однієї додаткової змінної x₅ та заміною зводимо задачу до вигляду

Розв´язуючи систему основних обмежень стандартної задачі відносно m базових змінних та виключаючи їх одночасно з цільової функції, дістаємо канонічну форму стандартної задачі, а саме:

(3.39)

(3.40)

(3.41)

;

де , а - значення цільової функції при даному базовому розв’язку . Тут базовими є останні m змінних.

Встановимо потрібний надалі зв’язок між деякими елементами стандартної задачі та її канонічною формою. Користуючись виразами (3.40), виключимо з цільової функції стандартної задачі (3.33) базові змінні канонічної задачі (3.39) – (3.41). Шляхом підстановки одержимо:

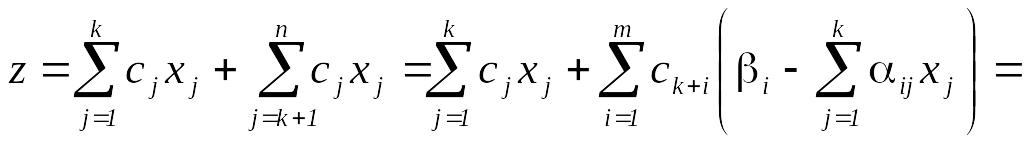
(3.42)

Отже, ;

де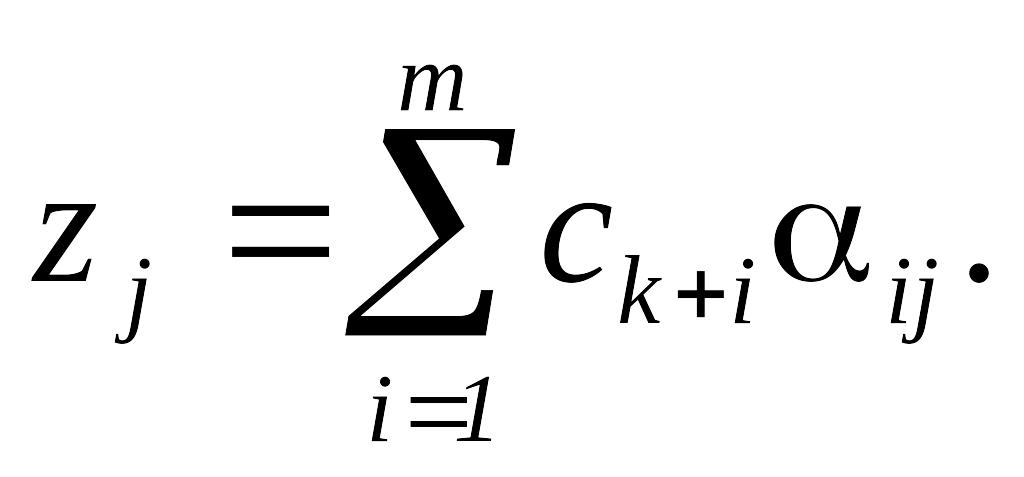 (3.43)

Очевидно, одержані формули можна використати для контролю обчислень при переході від стандартної задачі до канонічної, від одного базового розв’язку до іншого в канонічній задачі.

Основні обмеження канонічної задачі (3.40) легко представити у вигляді однорідної системи нерівностей, відкинувши в лівих частинах невід’ємні базові змінні. Одержимо таку еквівалентну задачу лінійного програмування:

(3.44)

(3.45)

;

(3.46)

Помноживши цільову функцію та кожне з основних обмежень на (-1), одержимо задачу мінімізації з однорідними обмеженнями-нерівностями типу “ ” (не менше),

(3.47)

(3.48)

;

(3.49)

Підкреслюючи тісний зв’язок задач (3.44) – (3.46) та (3.47) – (3.49) з канонічною формою стандартної задачі, будемо називати їх другою канонічною формою задач лінійного програмування. Задачі (3.44) – (3.46), (347) – (3.49) називають також симетричними задачами лінійного програмування.

Користуватись задачами з обмеженнями-нерівностями зручно при дослідженні важливих властивостей задач лінійного програмування, зокрема при геометричній їх інтерпретації та геометричному розв’язуванні найпростіших задач.