
- •Тема 1. Робочий зошит 3
- •Передмова
- •Робочий зошит
- •1. Вирішення економіко-математичних задач методами лінійного програмування
- •1.1. Симплексний метод
- •1.2. Метод потенціалів
- •Аналіз рішення
- •2. Економіко-математичні моделі для розрахунку оптимальних планів розвитку рослинництва
- •2.1. Економіко-математична модель оптимізації структури посівних площ
- •Розподіл продукції рослинництва і вихід живильних речовин
- •2.2. Економіко-математична модель оптимізації розподілу мінеральних добрив
- •Тема 2. Основні задачі статистичного моделювання Основна література.
- •Умова задачі.
- •2. Нормативні рівні чинників та результативного показника:
- •Варіанти задачі
- •Приклад виконання задачі.
- •1. Умова задачі.
- •2. Приклад рішення задачі.
- •2.2. Визначити нормативні розрахунки рівнів чинників та результативного показника
- •Нормативні розрахунки
- •Тема 3. Задачі лінійного програмування і їх застосування в управлінні сільськогосподарським виробництвом
- •1. Загальні рекомендації
- •2. Теоретичні питання
- •Задача 2
- •Загальна характеристика симплексного методу.
- •Алгоритм симплексного методу
- •Умова задачі.
- •Задача 3 Транспортна задача лінійного програмування. Загальна постановка задачі.
- •Умова задачі.
- •Задача 4. Економіко-математична модель оптимізації структури посівних площ. Загальна постановка задачі.
- •Умова задачі.
- •Рішення.
- •Задача 2. Симплексний метод розв’язання задач лінійного програмування. Умова задачі.
- •Рішення
- •Задача 3. Розв’язання транспортної задачі лінійного програмування. Умова задачі.
- •Рішення.
- •Задача 4. Економіко-математична модель оптимізації структури посівних площ. Умова задачі.
- •Рішення.
- •Задача 5 Економіко-математична модель оптимізації виробничої структури садового агропромислового підприємства
- •2. Початкова інформація
- •3. Система змінних моделі
- •Система обмежень моделі
- •Множини:
- •Шукані змінні:
- •Техніко-економічні коефіцієнти при змінних і вільні члени:
- •По технологічним взаємостосункам:
- •5. Аналіз оптимального рішення
- •Варіанти завдань для складання економіко-математичної моделі оптимізації виробничої структури агропромислового підприємства
- •Тема 4. Теорія ігор
- •2. Завдання 1.
- •Тема 5. Використання теорії графів.
- •Тема 6. Поняття про експертні системи експертні системи «корал»
- •1. Мета заняття
- •2. Зміст теми
- •Область Експерта
- •Область Користувача
- •3. Завдання
- •Термінологічний словник.
- •7. Література
- •Типова программа дисципліни «Моделювання технологічних процесів і систем» для студентів напряму підготовки 6.090101 “Агрономія” передмова
- •Теоретичні заняття
- •Список рекомендованої літератури
- •Економіко-математична модель оптимізації виробничої структури господарства.
- •Рішення завдань лінійного програмування за допомогою Excel Блок-схема рішення задачі
- •3.3.2. Введення умов задачі
- •Алгоритм 3.3.1. Уведення даних для рішення задачі лінійного програмування
- •Алгоритм 3.3.2. Робота в діалоговому вікні Пошук рішення
- •1. Сервіс, Пошук рішення...
- •4. Додати...
- •3.3.3. Рішення задачі
- •Алгоритм 3.3.3. Рішення задачі лінійного програмування
- •1. Параметри...
- •Максимальний час
- •Граничне число ітерацій
- •4. Виконати.
- •3.3.4. Графічне представлення результатів рішення
- •3.3.5. Подолання несумісності
- •Алгоритм 3.3.4. Зміна умов задачі
- •Алгоритм 3.3.5. Подолання несумісності
- •2. Сервіс, Пошук рішення...
- •6. Виконати.
- •3.3.6. Усунення необмеженості цільової функції
- •Моделювання в апк
- •Частина 2. Моделювання технологічних процесів
- •І систем. Практикум.
- •Навчальний посібник
2.2. Визначити нормативні розрахунки рівнів чинників та результативного показника
Для нормативних розрахунків метод статистичних рівнянь залежностей дозволяє відібрати тільки два чинника з п'яти: "Збір овочів з 1га" та "Собівартість 1ц овочів", де коефіцієнти стійкості зв'язку відповідають тесту стійкої залежності, тобто вони вищі за 0,7.
Традиційний метод кореляційного та регресійного аналізу також підтверджує вибір цих чинників значеннями коефіцієнтів їх кореляції із збитковістю вирощування овочів. Так, коефіцієнт кореляції між чинником "Збір овочів з 1га" та рівнем збитковості дорівнює - 0,71, а цей показник тісноти зв'язку між чинником "Собівартість 1ц овочів" та їх збитковістю становить +0,785. Отже, у першому випадку коефіцієнт кореляції свідчить про обернену залежність, а у другому - про пряму. Відмітимо тут також і те, що параметри одночинникової регресії для чинників "Збір овочів з 1га" та "Собівартість 1ц овочів" є від'ємними, тобто у другому випадку маємо різницю в знаках плюс та мінус між параметром регресії та коефіцієнтом кореляції.
Після відбору чинників, які забезпечать проведення достовірних нормативних розрахунків, виконуємо поставлені у п.2 задачі, питання.
Для вирішення п. 2а задачі, тобто обчислення нормативного рівня збитковості овочів при зміні їх урожайності на 1ц, розрахунки проводимо таким чином:
1) визначимо різницю коефіцієнта порівняння чинника "Збір овочів з 1га" при його зниженні на 1ц за формулою:
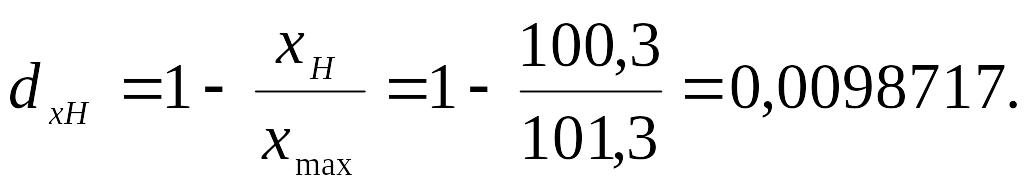
2) нормативний рівень збитковості вирощування овочів обчислимо за формулою:
![]()
Отже, зменшення збору овочів з 1га на 1ц зумовить зростання збитковості на +0,77% (1,97-1,2).
Традиційний метод регресійного аналізу свідчить про те, що при зростанні урожайності овочів на 1ц, збитковість їх вирощування зменшиться на 0,664%, якщо рівні всіх інших чинників прийняти незмінними.(Залишити на незмінному рівні всі інші чинники неможливо, бо це означало б зупинення їх розвитку.)
Для обчислення розміру зміни урожайності овочів з 1га при зміні збитковості їх вирощування на 1% проводимо такі розрахунки:
1) обчислимо різницю коефіцієнта порівнянні збитковості вирощування овочів при її зростанні на 1% за формулою
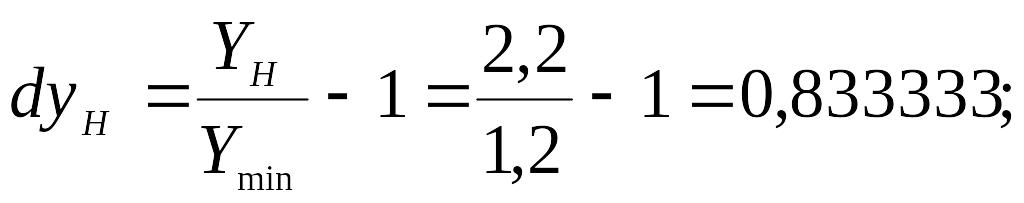
2) нормативний рівень збору овочів з 1 га буде дорівнювати:

Отже, зростання збитковості вирощування овочів на 1% буде зумовлено зниженням урожайності овочів на 1,31ц (99,99-101,3).
Аналогічні розрахунки проведемо також і по чиннику "Собівартість 1ц овочів". Тут для вирішення задачі: "На скільки зміниться рівень збитковості вирощування овочів при зростанні собівартості 1ц овочів на 1грн.?" проведемо такі розрахунки:
1) рівень собівартості 1ц овочів при його зростанні на 1грн. складе 22,26 (21,26+1). Отже, різниця коефіцієнтів порівняння складе:
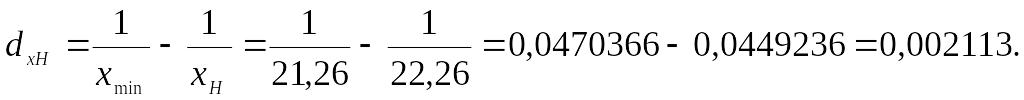
2) нормативний рівень результативної ознаки (рівня збитковості) буде дорівнювати:
![]()
Отже, при зростанні собівартості1 ц овочів на 1грн. рівень збитковості вирощування овочів зросте на 5,03% (6,23-1,2).
Якщо ж ставиться задача "На скільки зміниться рівень собівартості 1ц овочів при зростанні рівня збитковості на 1%?". то проводимо такі обчислення:
1) різниця коефіцієнта порівняння результативної ознаки (рівня збитковості) складе

2) нормативний рівень собівартості 1 ц овочів буде визначено за формулою
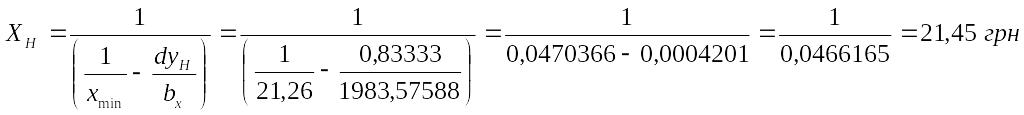
Отже, зростання рівня збитковості вирощування овочів на 1% зумовлює підвищення собівартості 1ц на 0,19грн. (21,45-21,26).
Традиційний метод регресійного аналізу при проведенні нормативних розрахунків дав такі результати:
1) при зростанні рівня собівартості 1ц овочів на 1грн. рівень збитковості знизиться на мінус 1932,67 одиниць, розділених на значення чинникової ознаки (х). Це означає, що при зростанні значень собівартості 1ц овочів по сільськогосподарських підприємствах окремих адміністративних районів, рівень збитковості буде зростати, але на меншу величину в залежності від рівня собівартості (х).
2) при множинній регресії (у поєднанні чотирьох чинників) виходить, що зростання собівартості 1ц овочів на 1грн. зумовлює зростання рівня збитковості на 0,91474%. Якщо ж поєднати чинник "Собівартість 1 ц овочів, грн." з всіма іншими чинниками ("Збір овочів з 1га", "Затрати праці на 1ц." і "Затрати на 1га посівів" та "Ціна реалізації 1ц"), то із зростанням собівартості 1ц овочів на 1грн. рівень збитковості зросте на 0,98408%.
Проведені обчислення нормативних рівнів чинників та збитковості вирощування овочів помістимо у табл. 7.
Порівнявши за даними табл. 7 нормативні розрахунки зміни рівнів чинників та результативного показника, можна стверджувати, що метод статистичних рівнянь залежностей дає більш широку інформацію про взаємозв'язок збитковості вирощування овочів з чинниками, що її формують.
Крім того, порівняння результатів вирішення задачі "На скільки зміниться рівень збитковості при зміні чинника на одиницю?", яка розв'язується обома методами, свідчить про різні варіанти, їх інтерпретації, які одержані за параметрами рівнянь традиційного методу регресійного аналізу. Так, якщо при інтерпретації першого чинника "Збір овочів з 1га" параметр лінійної парної регресії означає зниження збитковості вирощування овочів на 0,664% при зростанні збору овочів з 1га на 1ц, то для четвертого чинника "Собівартість 1ц овочів" такий же параметр гіперболічної функції характеризує зростання збитковості вирощування овочів на мінус 1932,67 одиниць розділених на значення х при збільшенні собівартості 1ц на 1грн. Підкреслимо, що такі результати одержані за даними параметрів одночинникових (парних)рівнянь регресії, підтверджених критеріями на достовірність (Фішера та Стьюдента). В той же час, підтверджені на достовірність за критерієм Фішера параметри цих чинників у множинних рівняннях регресії одержують різні значення, а їх розрахунок може бути здійснений тільки шляхом переходу до лінійного рівняння множинної регресії.
Таблиця 7
Порівняльна таблиця нормативних розрахунків рівнів чинників та результативного показника, виконаних методом статистичних рівнянь залежностей та регресійним аналізом
Символ |
Чинник |
Метод |
Задачі |
|
На скільки зміниться рівень збитковості при зміні чинника на одиницю |
На скільки зміниться рівень чинника при зміні рівня результативного показника (рівня збитковості) на одиницю |
|||
X1 |
Збір овочів з 1га, ц |
Статистичні рівняння залежностей (одночинникове і множинне) |
При зниженні збору овочів на 1ц: +0,77 |
При зростанні збитковості на 1%: -1,31ц |
Регресійний од-ночинниковий аналіз |
При зростанні збору овочів на 1 ц.: -0,664% |
X1 |
||
X4 |
Собівартість 1ц овочів, грн. |
Статистичні рівняння залежностей (одночинникове і множинне) |
При зростанні собівартості на 1грн: +5,03% |
При зростанні збитковості на 1%: +0,19 грн. |
Регресійний од-ночинниковий аналіз |
|
X1 |
||
Крім
того, тут часто змінюються також знаки
(плюс і мінус) при параметрах. У нашому
прикладі по чиннику "Збір овочів з
1га" спостерігається тільки зміна
значень параметрів від -0,664 при парній
регресії до мінус 0,156 - при множинній
регресії, а по чиннику "Собівартість
1ц овочів" відмічаємо не тільки різні
значення параметрів, але і різні знаки
при них (від мінус
![]() при парній регресії до плюс 0,915 – при
множинній регресії).
при парній регресії до плюс 0,915 – при
множинній регресії).
Додатки.
Формули розрахунків методу статистичних рівнянь залежностей.
Одночинниковий лінійний зв’язок
Прямий при:
а) збільшенні чинникової та результативної ознак
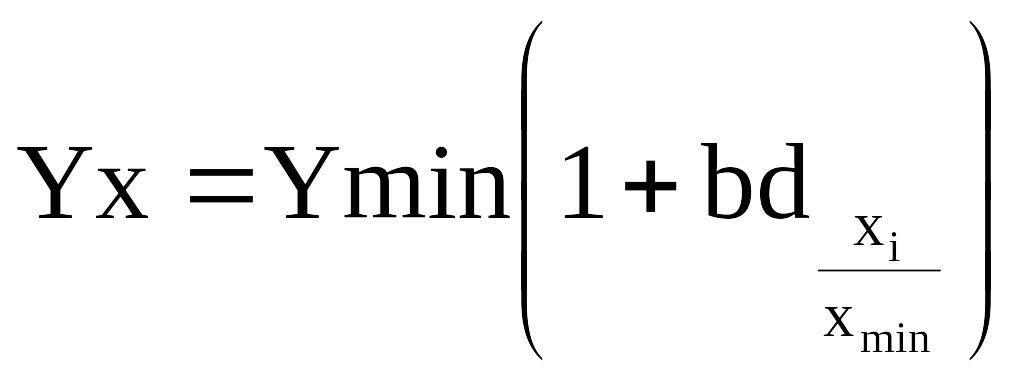 ;
;
б) зменшенні чинникової та результативної ознак
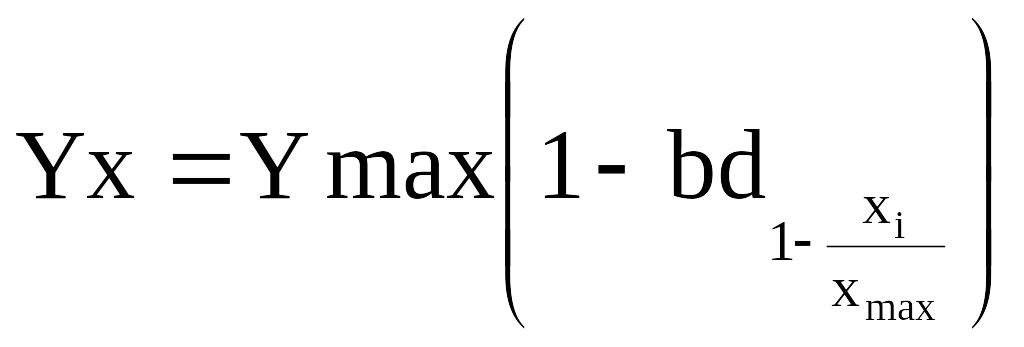 ;
;
Обернений при:
а) збільшенні чинникової ознаки і зменшенні результативної
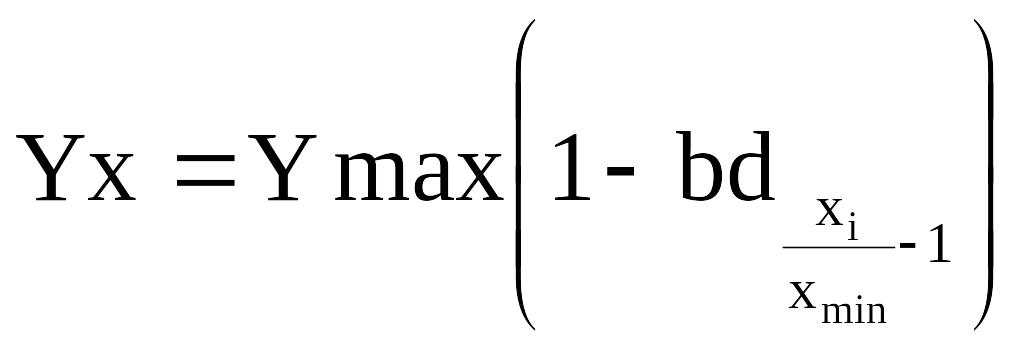
б) зменшення чинникової ознаки і збільшення результативної
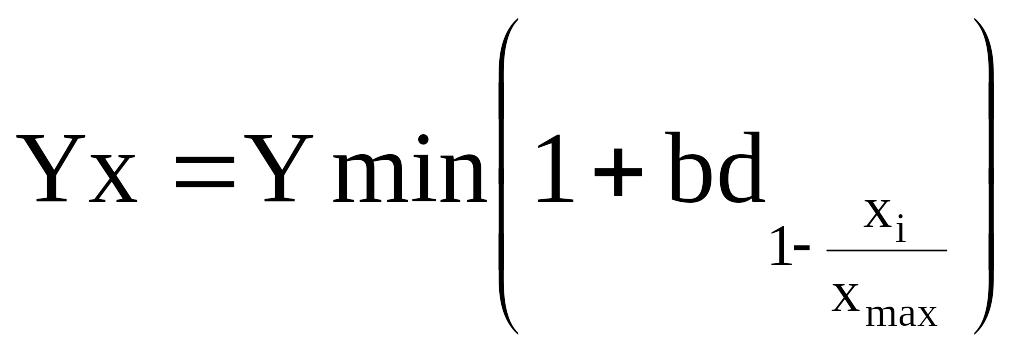
Одночинниковий криволінійний зв’язок
1. Парабола
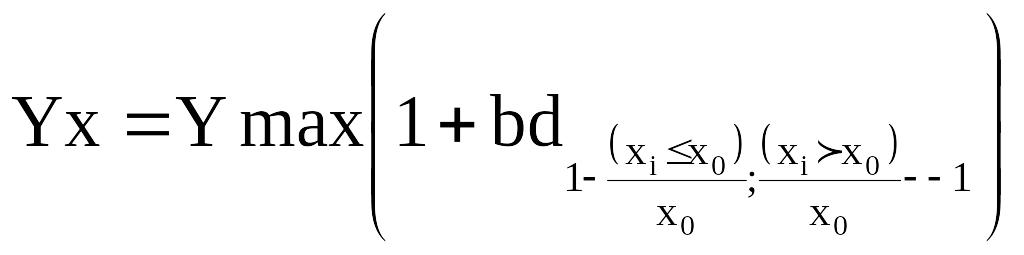
2. Обернена парабола
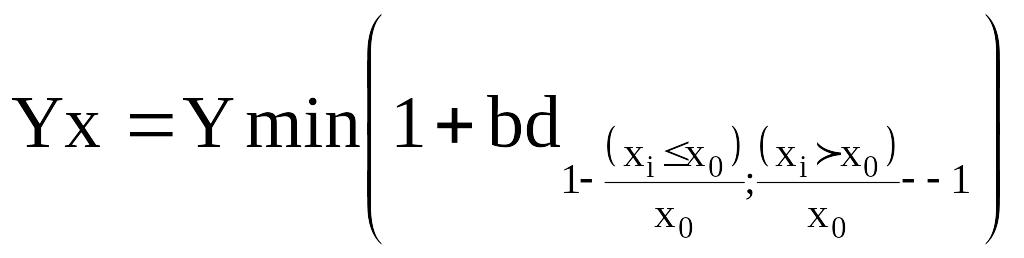
Гіпербола
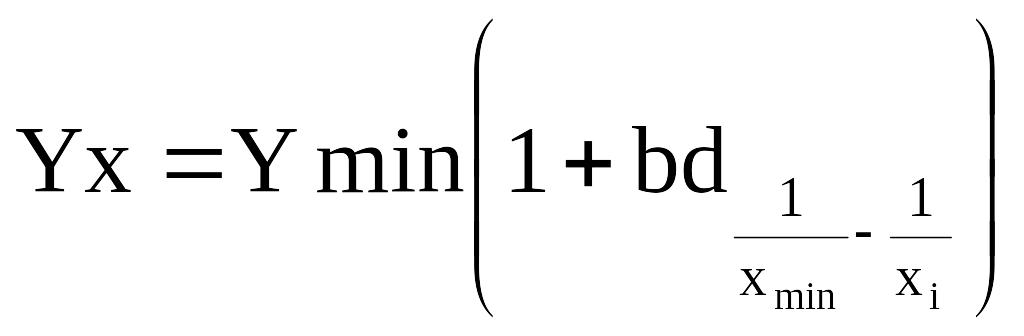
Обернена гіпербола

Логічна
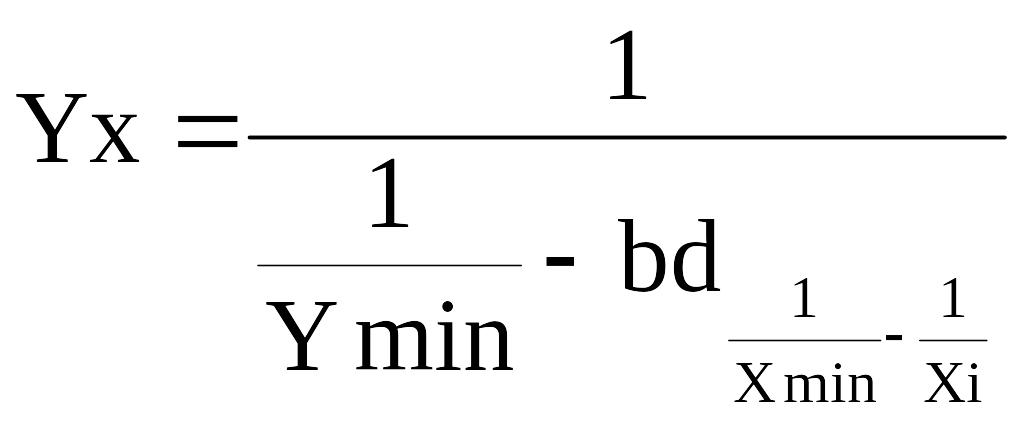
Обернена логічна

Багаточинниковий лінійний зв’язок
1. Прямий при:
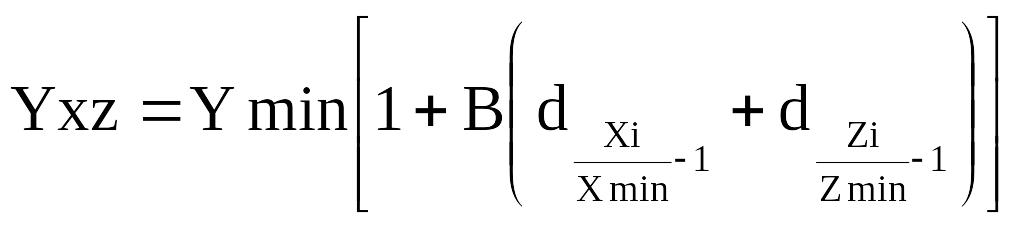
2. Обернений при:
а) збільшенні чинникових ознак і зменшенні результативної
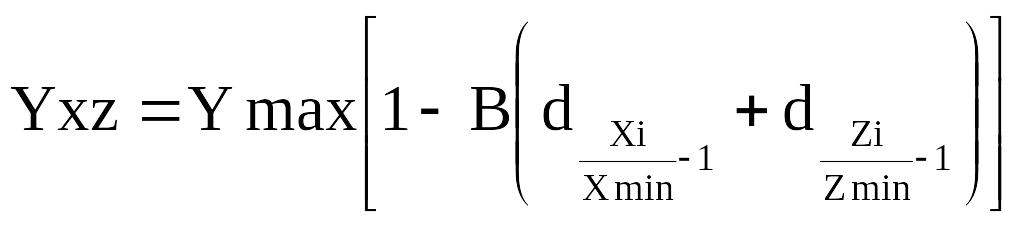
б) зменшенні чинникових ознак і збільшенні результативної
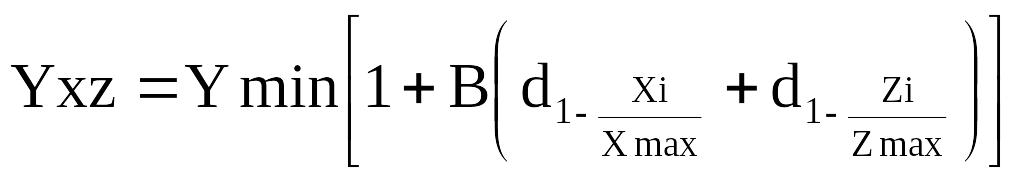
в) зменшенні чинникових і результативних ознак

3. Комбінаційний при:
а) прямій залежності Y від Х і оберненій залежності Y від Z:
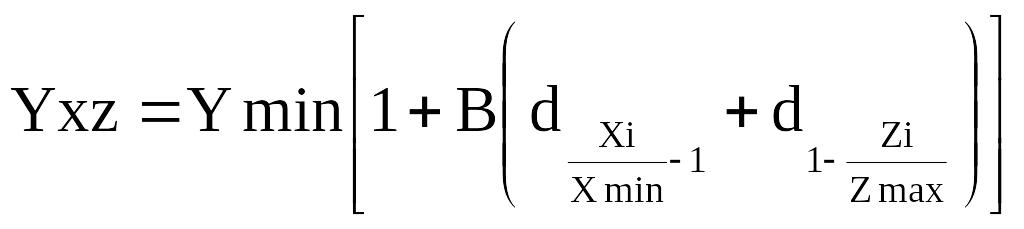
б) оберненій залежності Y від Х і прямій залежності Y від Z:
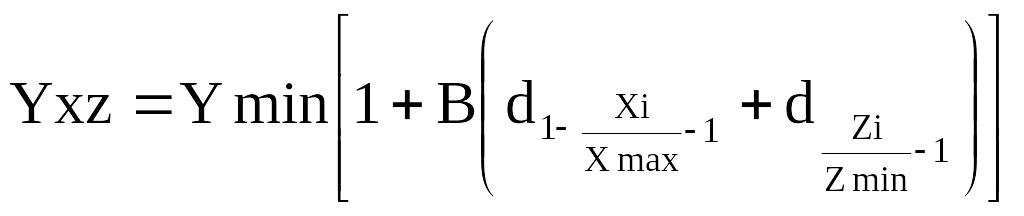
Багаточинниковий криволінійний зв’язок
1. Парабола
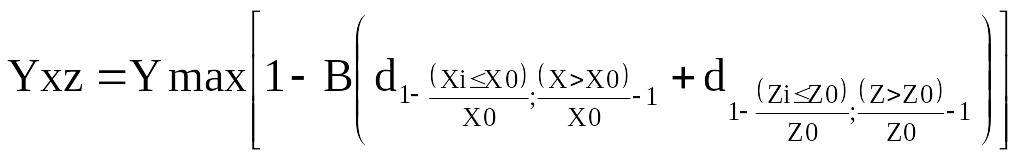
2. Обернена парабола
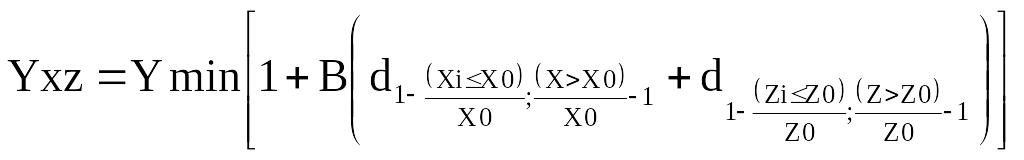
3. Гіпербола

4. Обернена гіпербола
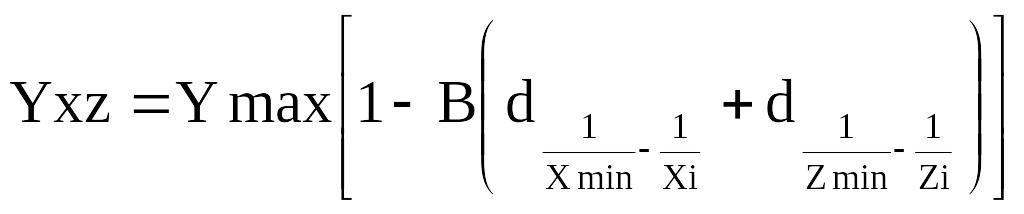
Логічна

Обернена логічна
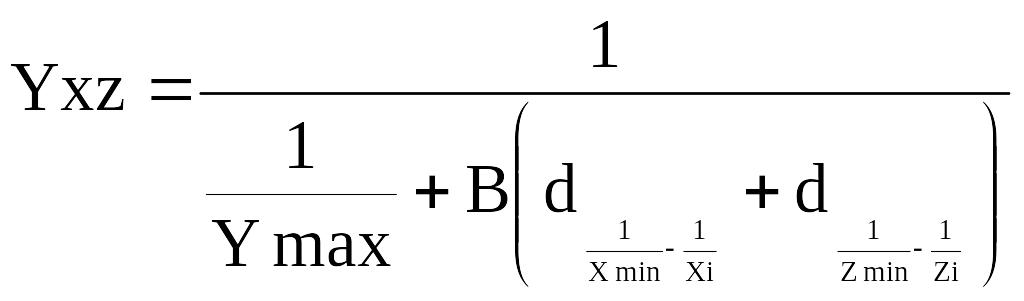
Параметри залежності
а) одночинникової
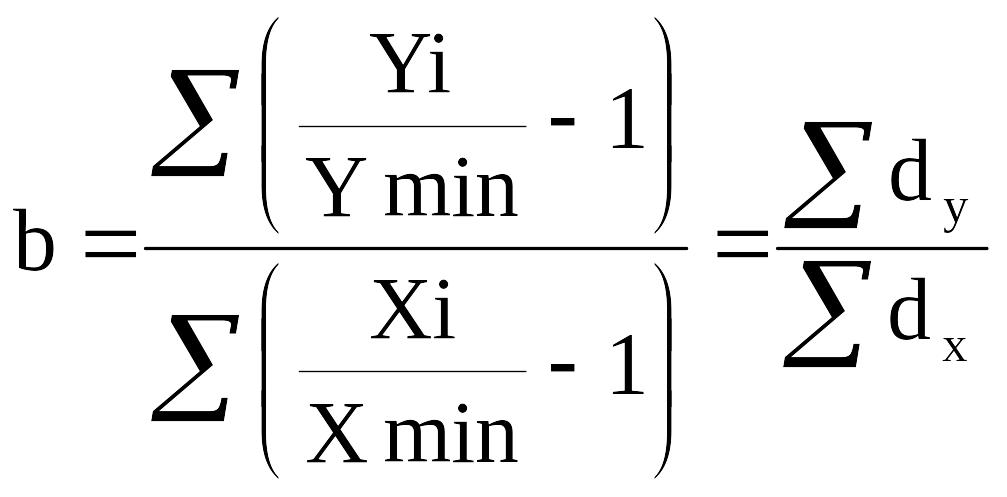
б) багаточинникової
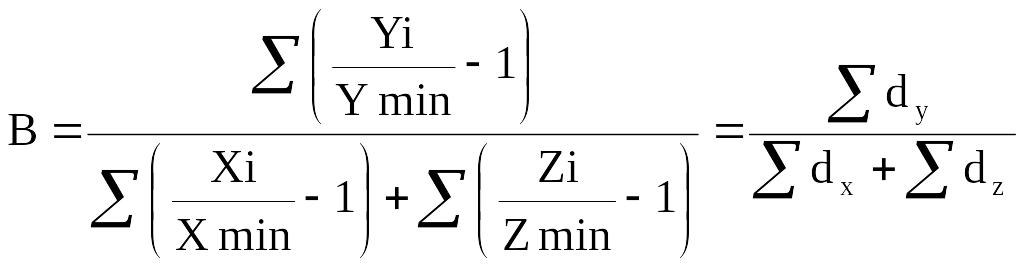
Коефіцієнт кореляції одночинниковий
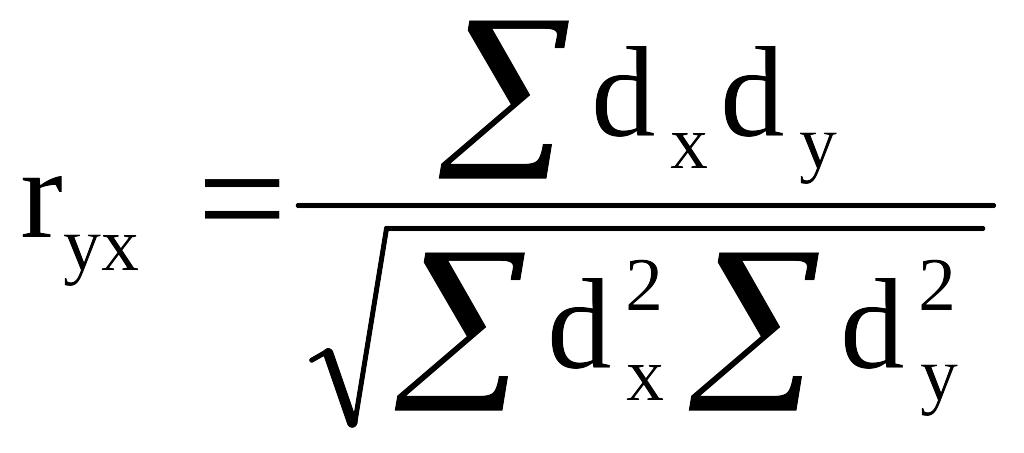
Індекс кореляції (одночинниковий і багаточинниковий)
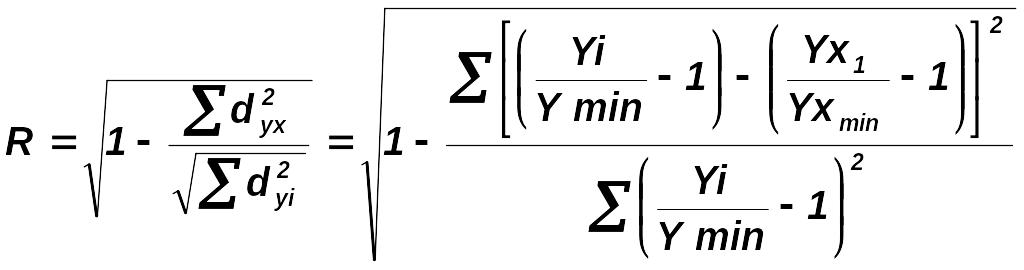
Коефіцієнт стійкості зв’язку
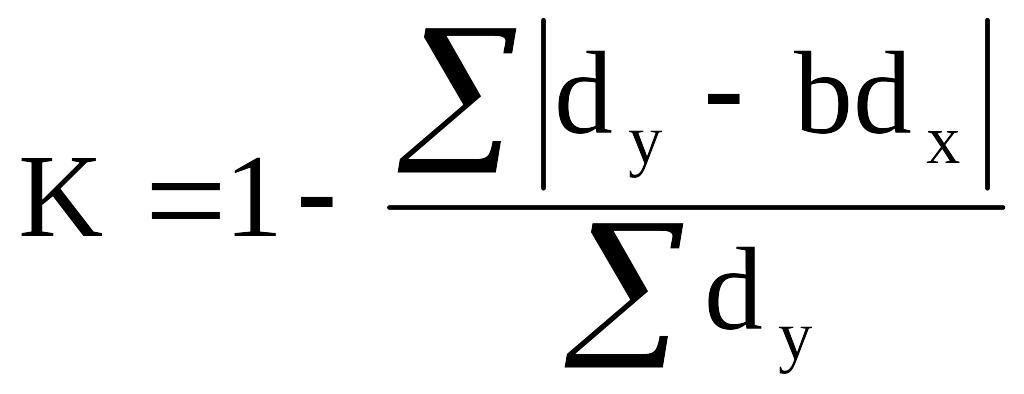
Шкала оцінки залежностей
Критерії оцінки |
Коефіцієнт стійкості зв’язку |
Нестійкий зв’язок |
|
дуже низький |
до 0,5 |
низький |
0,5-0,6 |
помітний |
0,6-0,7 |
Стійкий зв’язок |
|
середній |
0,7-0,8 |
високий |
0,8-0,9 |
дуже високий |
0,9 і більше |
