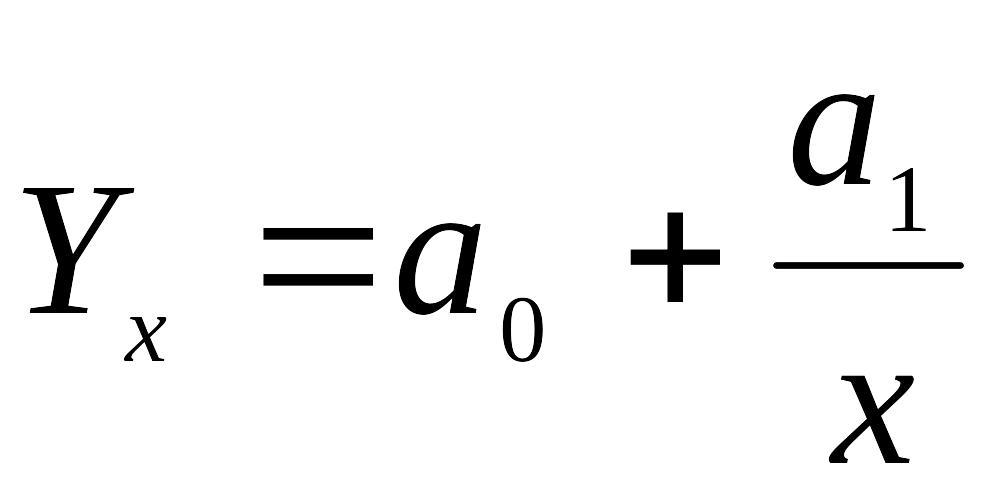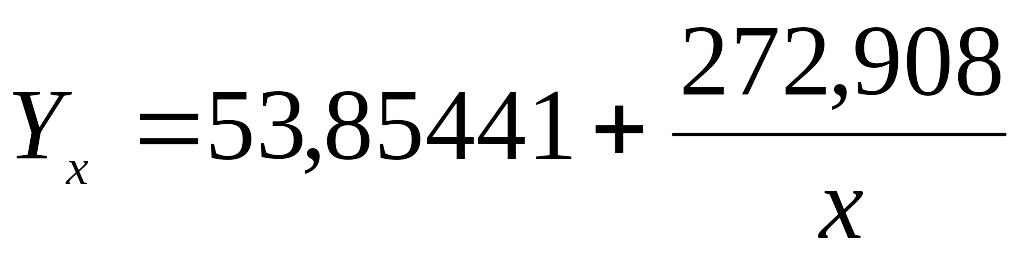Приклад виконання задачі.

1. Умова задачі.

Збитковість вирощування овочів у сільськогосподарських підприємствах та рівні чинників, що її формують в адміністративних районах області, характеризуються такими даними за рік:

№ району	Збір овочів з 1га, ц	Затрати праці, людино-годин на 1ц	Затрати на 1га посіву, грн.	Собівартість 1ц, грн.	Ціна реалізації 1ц, грн.	Рівень збитковості, %
	52,8	47,4	1549	31,84	21,83	31,4
	72,6	16,1	1694	32,30	19,09	40,9
	50,4	31,7	1807	32,21	20,26	37,1
	33,4	29,3	1615	48,95	28,57	45,7
	31,5	30,9	1426	42,48	17,96	57,7
	54,6	25,6	1542	35,38	15,32	66,7
	54,3	19,2	1309	29,11	20,19	13,3
	36,6	36,3	2093	67,07	24,26	63,8
	15,6	46,2	1136	65,52	20,47	68,8
	73,2	7,3	1649	21,26	20,67	2,8
	65,9	16,8	1601	31,29	18,95	39,4
	44,6	22,8	1560	33,63	24,81	26,2
	23,7	16,6	2213	73,35	22,92	68,8
	64,6	16,4	2228	40,12	26,49	34,0
	25,6	26,5	1334	43,63	22,83	47,6
	47,2	26,0	1366	32,20	18,13	43,7
	38,2	12,4	1324	49,85	28,14	43,6
	64,1	10,0	2139	39,02	23,47	39,9
	30,3	41,7	1517	41,70	20,85	50,0
	28,4	67,9	1470	49,53	28,17	43,1
	47,8	22,4	1732	38,00	21,20	44,2
	101,3	30,2	2459	22,14	21,87	1,2
	61,4	39,6	2239	44,17	20,83	52,8
	67,6	18,4	2094	31,40	20,00	20,2

2. Приклад рішення задачі.

2.1. Визначити параметри та критерії методу статистичних рівнянь залежностей:

Шляхом побудови графіків та перебору одночинникових рівнянь залежностей для характеристики впливу вибраних чинників на рівень збитковості вирощування овочів відібрані такі їх види та напрямки (таблиці та графіки 1-5).

Таблиця 1 Вид та напрямок залежності збитковості вирощування овочів від різних чинників

Символ чинника	Чинник	Вид та напрямок зв'язку	№ графіка
X1	Збір овочів з 1 га, ц	лінійний, обернений зв’язок (зростання Y, зниження X)	1
X2	Затрати праці на ц, людино-годин	гіпербола, зв'язок прямий	2
X3	Затрати на 1 га посівів, грн.	логарифмічна функція, обернений зв'язок	3
X4	Собівартість 1 ц овочів, грн.	гіпербола, зв'язок прямий	4
X5	Ціна реалізації 1 ц овочів, грн.	гіпербола, зв'язок обернений	5

Отже, згідно з табл.1 та графіками 1-5 видно, що:

1. зниження значень чинника "Збір овочів з 1га, ц" зумовлює зростання рівня збитковості їх вирощування (рис. 1)

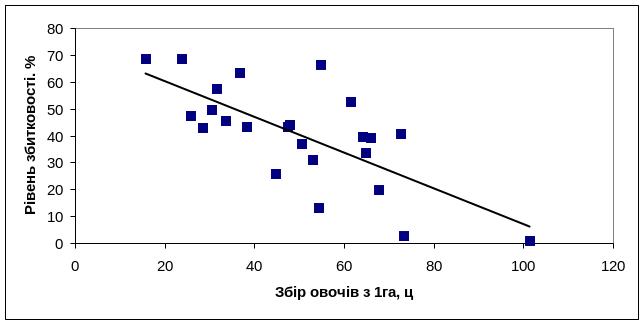
Рис.1. Залежність збитковості вирощування овочів від їх урожайності

2. збільшення значень чинника "Затрати праці на 1ц овочів, людино-годин" зумовлює зростання рівня збитковості вирощування овочів до якоїсь межі, за якою воно припиняється, залишаючись майже на одному рівні (рис.2.)

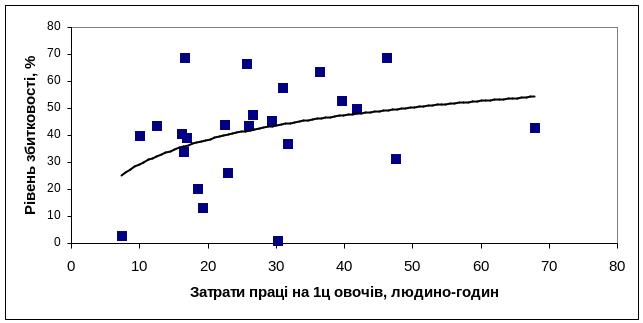
Рис. 2. Залежність збитковості вирощування овочів від затрат праці на 1 ц, людино-годин

3. зростання значень чинника "Затрати на 1 га посівів овочів, грн." сприяє зниженню рівня збитковості їх вирощування (рис. 3):

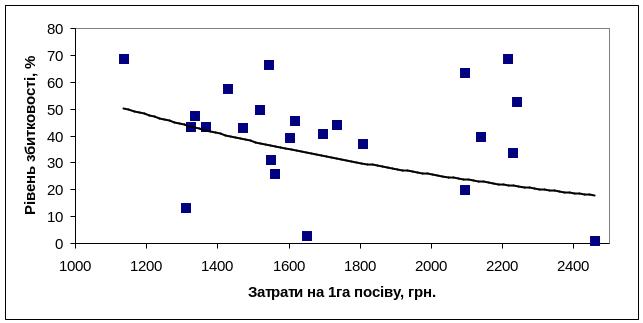Рис.3. Залежність збитковості вирощування овочів від затрат на 1 га посівів, грн.

4. зростання значень чинника "Собівартість 1 ц овочів, грн." зумовлює спочатку зростання рівня збитковості їх вирощування, а потім цей показник залишається на одному рівні (рис.4):

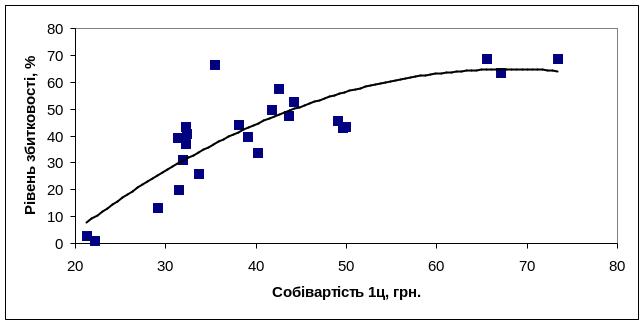Рис.4. Залежність збитковості вирощування овочів від рівня собівартості 1ц

5. зростання значень чинника "Ціна реалізації 1ц овочів, грн." зумовлює спочатку зниження рівня збитковості, а потім цей показник, досягнувши якоїсь межі, залишається майже на одному рівні (рис.5):

Рис.5. Залежність збитковості вирощування овочів від ціни їх реалізації

Для характеристики параметрів та критеріїв одночинникових рівнянь залежностей побудуємо табл.2.

Згідно з шкалою залежностей стійким вважається вплив при значенні коефіцієнта від 0,7 до 1,0. Якщо ж стійкість впливу чинника менша 0,7 то його не можна використовувати для нормативних чи прогнозних розрахунків, тому що одержані результати будуть недостовірними.

За даними табл.2 стійкий вплив на формування збитковості вирощування овочів мають такі чинники, як "Збір овочів з 1га, ц" та "Собівартість 1ц овочів, грн.", де коефіцієнти стійкості зв'язку дорівнюють відповідно 0,741 та 0,819.

Згідно з критеріями вибору форми функції потрібно щоб значення коефіцієнта та індексу кореляції співпадали (їх різниця не повинна перевищувати 0.01), а також була найменшою сума лінійних відхилень теоретичних значень результативної ознаки від їх фактичних величин .

Таблиця 2

Параметри та критерії одночинникової залежності

Символ чинника	Чинник	Показник
		параметр залежності	коефіцієнт стійкості	коефіцієнт кореляції	індекс кореляції	сума відхилень
		b	k	r	R
Х1	Збір овочів з 1га,ц	64,666352	0,741	0,955	0,955	247,3S
Х2	Затрати праці, людино-годин на 1ц	443,14909	0,675	0,919	0,919	310,41
Х3	Затрати на 1 га посіву, грн.	71,4606	0,446	0,789	0,774	370,22
Х4	Собівартість 1 ц овочів, грн.	1983,5759	0,819	0,977	0,977	172,8
Х5	Ціна реалізації, 1ц, грн.	1481,8182	0,415	0,803	0,798	390,65

За цими критеріями правильно підібраними вважають види і напрямки зв'язку всіх включених до розрахунків чинників, окрім чинника "Затрати на 1га посівів овочів, грн.", де різниця між коефіцієнтом та індексом кореляції складає 0,015(0,789-0,774).

Для розрахунку параметрів одночинникового рівняння залежності при відсутності можливості комп'ютерного опрацювання візьмемо чинник "Збір овочів з 1га, ц" та визначимо його вплив на "Рівень збитковості вирощування овочів, %".

Рівняння одночинникової лінійної оберненої залежності тут має такий вигляд:

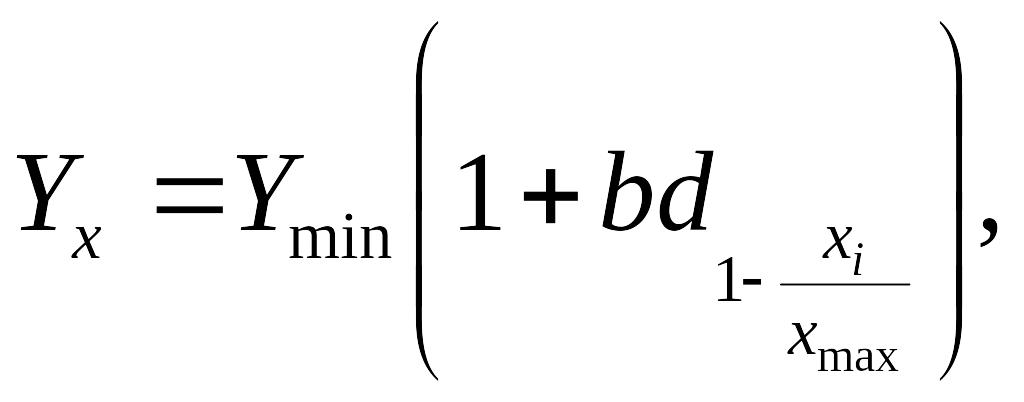
де Y_x - рівняння одночинникової залежності;

Y_min- мінімальне значення результативної ознаки (рівня збитковості);

х_i- значення чинникової ознаки (збору овочів з 1 га, ц)

х_max- максимальне значення чинникової ознаки;

b - параметр залежності;

d - знак відхилень.

Для розрахунків побудуємо табл.3.

За даними табл.3 параметр рівняння лінійної оберненої залежності складе:

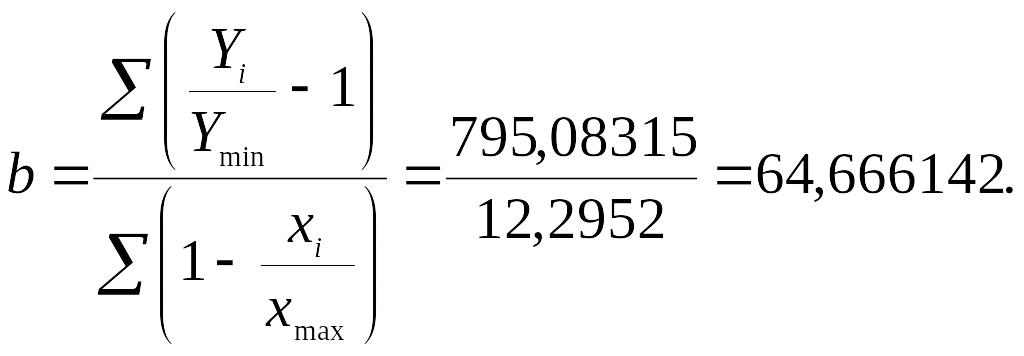
Таблиця 3.

Розрахунок параметрів одночинникового рівняння лінійної оберненої залежності (зростання Y, зниження X)

№ району	Збір овочів з 1га, ц	Рівень збитковості, %	dx	dy	bdx	Теоретичні значення рівня збитковості, % Yx
	52,8	31,4	0,4788	25,1667	30,9621	38,35
	72,6	40,9	0,2833	33,08333	18,3199	23,18
	50,4	37,1	0,5025	29,91667	32,4947	40,19
	33,4	45,7	0,6703	37,08333	43,3457	53,21
	31,5	57,7	0,6890	47,08333	44,555	54.67
	54,6	66,7	0,461	54,58333	29,8111	36,97
	54,3	13,3	0,464	10,08333	30,0051	37,21
	36,6	63,8	0,6387	52,1667	41,3023	50,76
	15,6	68,8	0,846	56,3333	54,7076	66,85
	73,2	2,8	0,2774	1,3333	17,9384	22,73
	65,9	39,4	0,3495	31,8333	22,6008	28,32
	44,6	26,2	0,5597	20,8333	36,193	44,63
	23,7	68,8	0,766	56,3333	49,5343	60,64
	64,6	34,0	0,3623	27,3333	23,4285	29,31
	25,6	47,6	0,7473	38,6667	48,325	59,19
	47,2	43,7	0,5341	35,41667	34,5382	42,65
	38,2	43,6	0,6229	35,3333	40,2805	49,54
	64,1	39,9	0,3672	32,25	23,7454	29,69
	30,3	50,0	0,7009	40,6667	45,3245	55,59
	28,4	43,1	0,7196	34,9167	46,5338	57,04
	47,8	44,2	0,5281	35,8333	34,1502	42,18
	101,3	1,2	0	0	0	1,2
	61,4	52,8	0,3939	43,0	25,472	31,77
	67,6	20,2	0,3327	15,8333	21,5144	27,02
Разом:		982,9	12,2952	795,08315		982,9"

Це означає, що зміна розміру відхилень коефіцієнтів порівняння чинникової ознаки на одиницю зумовлює збільшення розміру відхилень коефіцієнтів порівняння результативної ознаки в 64,666142 рази.

Рівняння лінійної оберненої залежності набуде вигляду:

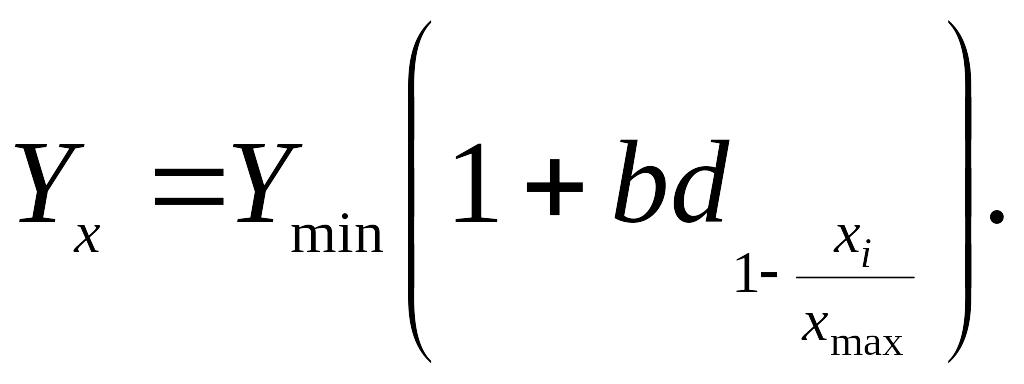
Звідси маємо:

Параметри цього рівняння дозволяють обчислити теоретичні значення рівня збитковості (Y_x)

1-й район

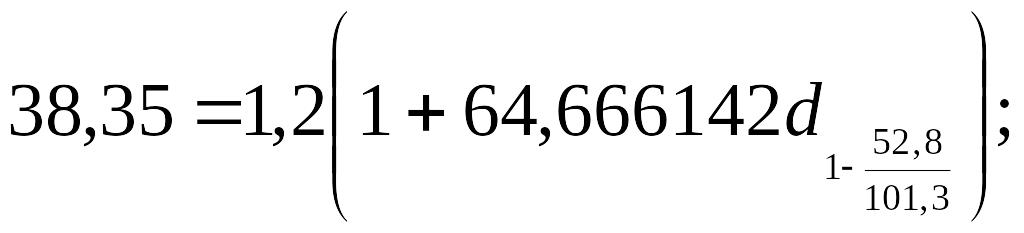
2-й район

і т.д.

Дані табл.4 дозволяють також обчислити такі показники, як коефіцієнт стійкості зв'язку, коефіцієнт та індекс кореляції, суму лінійних відхилень між фактичними і теоретичними значеннями результативної ознаки, побудувати графік одночинникової залежності та виконати нормативні розрахунки рівнів чинника та результативної ознаки.

Для вирішення п.1д задачі необхідно визначити параметри рівняння множинної залежності за однотипним видом одночинникових рівнянь.

У даному прикладі з 5-ти чинників, за тестом стійкості зв'язку, для проведення нормативних розрахунків було відібрано тільки два: "Збір овочів з 1 га" та "Собівартість 1ц овочів". Розрахунок параметрів одночинникових рівнянь залежностей тут здійснено за різними видами рівнянь (за рівнянням лінійного оберненого зв'язку для чинника "Збір овочів з 1га", та за рівнянням гіперболи - для чинника "Собівартість 1ц овочів". Метод статистичних рівнянь залежностей дозволяє переходити від одночинникових рівнянь до таких форм множинних рівнянь: лінійної, лінійної комбінаційної, гіперболи, параболи та логічної функції). Однотипним видом для множинного рівняння тут можна прийняти, як лінійну залежність, так і гіперболу, якщо кожний з чинників витримає тест на стійку залежність (коефіцієнт стійкості зв'язку повинен бути не менше 0,7).

Проте, звести ці два чинники у множинне рівняння лінійної залежності або гіперболи немає можливості, внаслідок відсутності стійкого зв'язку для одного з чинників. Так, при спробі звести у множинну залежність гіперболічний зв'язок чинника "Собівартість 1ц овочів" до лінійної залежності, коефіцієнт її стійкості знижується з 0,819 до 0,67, а якщо лінійну обернену залежність чинника "Збір овочів з 1га" замінити на обернену гіперболу, то коефіцієнт стійкості тут складає тільки 0,59 (замість значення 0,741 при одночинниковому лінійному оберненому зв'язку).

Такі значення коефіцієнтів стійкості зв'язку не забезпечують достовірності, як параметрів рівняння множинної залежності, так і частки впливу кожного з чинників на результативну ознаку. Отже, вважаємо, що визначати параметри множинного рівняння для п. 1д задачі недоцільно.

Порівняємо також застосування статистичних рівнянь залежностей в аналізі впливу різних чинників на рівень збитковості вирощування овочів з традиційним методом регресійного та кореляційного їх аналізу.

На відміну від методу статистичних рівнянь залежностей, де спочатку потрібно обчислити параметри рівнянь залежностей, а потім лише за моделями одночинникових рівнянь визначити з метою підтвердження правильності вибраного рівняння коефіцієнт та індекс кореляції, традиційний метод кореляційного та регресійного аналізу вимагає обчислення коефіцієнтів кореляції між змінними ознаками, тобто розрахунку матриці парних коефіцієнтів кореляції (табл.4).

Таблиця 4

Матриця парних коефіцієнтів кореляції

	X1	X2	X3	X4	X5	Y
X1	1,00000
X2	-0,41962	1,00000
X3	0,54810	-0,20898	1,00000
X4	-0.75032	0,29053	-0,00185	1,00000
X5	-0,18031	0,03691	0,18908	0,33369	1,00000
Y	-0,71221	0,30049	-0,18050	0,78524	-0,06034	1,00000

З даних табл.4 видно, що тісний зв'язок результативного показника (рівня збитковості) спостерігається тільки з такими чинниками як "Збір овочів з 1га" та "Собівартість 1ц овочів", де коефіцієнти кореляції дорівнюють - 0,71 та +0,785 відповідно. Як на те, між цими чинниками існує тісний обернений зв'язок (-0,75). Одним з критеріїв регресійного аналізу е відсутність лінійної залежності між чинниками, тобто мультиколінеарності. Отже, чинник "Збір овочів з 1га", або "Собівартість 1ц овочів" потрібно було б виключити з розрахунків, не зважаючи на їх важливість в оцінці впливу на рівень ефективності вирощування овочів.)

Проте, відомо, що відсутність тісного зв'язку між змінними величинами (навіть якщо коефіцієнт кореляції дорівнює нулю) зовсім не означає наявності між ними гіперболічної, параболічної та інших видів криволінійної залежності.

Обчислені традиційним методом значення параметрів парних та множинних рівнянь регресії наведені у табл.5.

Обчислені параметри у множинних рівняннях регресій підтверджені на їх достовірність за критерієм Фішера для всіх чинників (табл. 5). Значення цих параметрів свідчать про специфіку традиційного методу регресійного аналізу, при якому значення параметрів змінюються при зміні кількості включених до розрахунків чинників. Ця зміна часто супроводжується не тільки появою різних значень параметрів, але і знаків при них (плюс та мінус), як при переході від одночинникових рівнянь регресії, так і при збільшенні або зменшенні кількості чинників у множинних рівняннях, що видно із даних табл. 5.

Таблиця 5.

Параметри парних та множинних рівнянь регресії, обчислених методом найменших квадратів

Символ	Чинник	Параметри рівняння	Критерії Фішера для множинних рівнянь
			критичний	фактичний
X1	Збір овочів з 1га, ц	1.Одночинникового Yx =a0+a1x Yx=73,77513-0,66434x
X2	Затрати праці на 1ц, людино-годин	1. Одночинникового 2. Множинного	4,11	6,86
X3	Затрати на 1га посівів, грн.	1. Одночинникового 2. Множинного	3,30	6,30
X4	Собівартість 1ц овочів, грн.	1. Одночинникового 2. Множинного	2,94	6,80
X5	Ціна реалізації 1ц, грн.	1. Одночинникового 2. Множинного	2,78	8,78

Примітка: розрахунок множинних параметрів рівнянь виконуються під час проведення лабораторно-практичних занять із застосуванням ПЕОМ.

Критерії достовірності одночинникових регресійних рівнянь помістимо у табл. 6.

Таблиця 6

Порівняльна таблиця критеріїв достовірності одночинникових рівнянь регресій

Символ чинника	Чинник	Критерії
		Фішера		Стьюдента
		критичний	фактичний	критичний	фактичний
Х1	Збір овочів з 1га	4,22	22,65	2,08	-4,76
Х2	Затрати праці на 1ц, людино-годин	4,22	4,39	2,08	-2,09
Х3	Затрати на 1га посіву, грн.	4,22	0,78	2,08	-0,88
Х4	Собівартість 1ц овочів, грн.	4,22	62,76	2,08	-7,92
Х5	Ціна реалізації 1ц, грн.	4,22	0,32	2,08	0,57

З даних табл. 6 видно, що для оцінки впливу чинників на результативну ознаку (рівень збитковості вирощування овочів) можна відібрати такі чинники, як "Збір овочів з 1га", "Затрати праці на 1 ц овочів, людино-годин" та "Собівартість 1ц овочів", де моделі рівнянь регресії вважаються достовірними. (Фактичні значення критеріїв Фішера та Стьюдента перевищують їх критичні рівні.)

Тут відмітимо також і те, що по такому чиннику, як "Затрати праці на 1ц овочів, людино-годин" фактичні та критичні значення коефіцієнтів Фішера та Стьюдента майже співпадають. Метод статистичних рівнянь залежностей не дозволив відібрати цей чинник для проведення нормативних розрахунків за тестом стійкості зв'язку (0,675), тобто він тут також знаходиться майже на межі його відбору для проведення достовірних нормативних розрахунків (нижня межа критерію стійкості зв'язку дорівнює 0,7).