2. Сервіс, Пошук рішення...

3. Установити цільову комірку 14 рівної мінімальному значенню.

4. У вікно Змінюючи комірки увести ВЗ:НЗ.

5. У вікно Обмеження ввести обмеження і граничні умови:

В3=10	Е3>=0	19<=К9
С3=5	F3>=0	110<=К10
D3=6	G3>=0	I11<=K11
Н3>=0

6. Виконати.

На екрані: результат рішення, показаний на рис. 3.3.16.

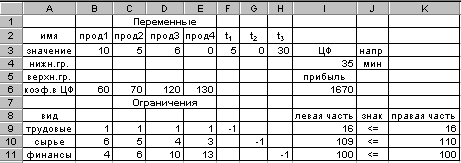
Рис. 3.3.16

З цього малюнка видно, що шуканий додатковий потрібний ресурс дорівнює t₁ = 5, t₂ = 0, t₃ = 30. Це значить, що для заданого випуску продукції необхідно мати усього наступна кількість ресурсів:

трудові	16+5=21
сировина	110+0=110
фінанси	100+30=130

При цьому буде отриманий прибуток, рівний 1670.

Важко переоцінити корисність такого підходу при виникненні несумісності. Якщо в реальних умовах ресурси збільшити немає можливості, то варто призначити граничні умови х, S 0, як це робилося у вихідній задачі, тоді буде отримане рішення, що визначається наявними ресурсами.

3.3.6. Усунення необмеженості цільової функції

У 3.2.1 ми розглядали систему (3.2.2). Додамо до системи цільову функцію, тоді одержимо:

F=x1 max x1 +x2 1 х1 0;Х2 0

  

який графічно була подана на рис. 3.2.2. Було показано, що задача (3.2.2) має необмежену цільову функцію. Подивимося, як буде вирішуватися така задача в Excel. Умови задачі у форматі, необхідному для її рішення в Excel, наведені на рис. 3.3.17.

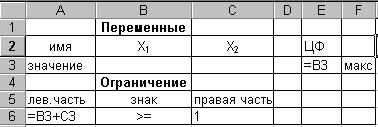
Рис. 3.3.17

У ході рішення цієї задачі на екрані з'являється діалогове вікно мал. 3.3.13, що, як ми вже знаємо, є ознакою необмеженості цільової функції. Для подолання цієї необмеженості необхідно при максимизації цільової функції область припустимих рішень обмежити зверху. З цією метою до (3.2.2) додамо обмеження

x₁+x_22,

після чого (3.2.2) буде мати вигляд:

F =x1мах x1 +x2 1 х1 +х22 x1 >0;x2 0

  

(3.3.4)

що графічно подано на рис. 3.3.18.

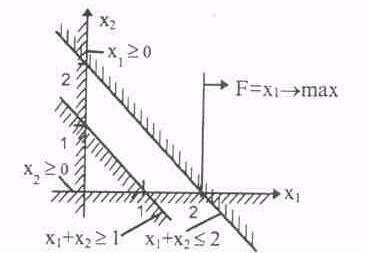
Ввод умов задачі (3.3.4) у формі уведення формул і у формі введення даних, а також результат її рішення наведені на мал. 3.3.19.

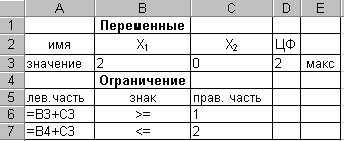
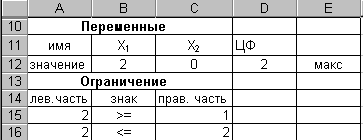
Рис. 3.3.19

Як видно з рис 3.3.19, після введення додаткового обмеження було отримано оптимальн рішення. Рішення цього приклада проілюструвало висновки, що ми зробили раніше при розгляді необмеженості цільової функції:

• Рішення буває не обмеженим у тому випадку, коли область припустимих рішень не має обмеження, що перешкоджає безкінечному зростанню (убуванню) цільової функції.

• При максимизації цільової функції область припустимих рішень повинна бути обмежена зверху.

• При мінімізації цільової функції область припустимих рішень повинна бути обмежена знизу.

Знаючи ці правила, легко усунути необмеженість цільової функції, ознакою якої являє поява на екрані діалогового вікна (рис. 3.3.13).

В’юненко Олександр Борисович