Алгоритм 3.3.4. Зміна умов задачі
1. Викликати вихідну таблицю (рис. 3.3.5).
2. По алг. 3.3.2 викликати діалогове вікно Пошук рішення.
3. Змінити граничні умови для Прод1:
У вікні Обмеження курсор на рядок $У$3>=$У$4.
Змінити...
На екрані: діалогове вікно Змінити обмеження.
Увести зміну: $У$3=10.
ОК.
4. Аналогічно ввести значення для Прод3: D3=6.
5. Увести додаткову умову для Прод2:
Додати.
Увести: С3=5.
ОК.
На цьому введення змін закінчено.
6. Вирішити задачу.
На екрані: діалогове вікно рис. 3.3.12.
Поява цього діалогового вікна - ознака несумісного рішення. Що ж робити в таких випадках? Звернемося до математичної моделі. Розглянута задача має модель:
-
F1 = 60х1 +70х2 +120х3 +130х4 max
х1+x2 +x3 +x4 16
6х1 + 5х2 + 4x3 + 3х4 110
4х1 +6х2+10х3+13х4 100
x1 = 10; x2 = 5; x3 = 6; x4 = 0
(3.3.1)
Для з'ясування причин несумісності введемо додаткові необхідні ресурси ti і запишемо систему у вигляді:
-
F2 = 60х1 + 70х2 +120х3 +130х4 min
x1 +x2 +x3 +x4 = 16+t1
6х1+5х2+4х3+3х4=110+t2
4х1+6х2+10х3+13х4 =100+t3
t1 0; t2 0; t3 0
(3.3.2)
Така постановка задачі дає можливість визначити мінімальне значення додаткових необхідних ресурсів t1, t2, t3.
Для введення умов задачі систему (3.3.2) запишемо у вигляді:
-
F = t1 +t2 +t3 min
x1+x2 +x3 +x4-t1 =16
6x1+5x2+4x3+3x4-t2 =110
4х1 +6х2+10х3 +13х4-t3 =100
t1 0; t2 0; t3 0
(3.3.3)
Щоб увести цю систему, відкоригуємо таблицю для введення даних (рис. 3.3.4) і зробимо її такою, як на рис. 3.3.14 (дані) і рис. 3.3.15 (формули).
Рис. 3.3.14 відрізняється від мал. 3.3.4 наступним:
уведено стовпці F:H для перемінних t1, t2, t3;
у комірках F9:H11 уведені - 1;
у комірці 16 залежність для прибутку збережена;
у комірку 14 уведена залежність для нової цільової функції, що мінімізується.
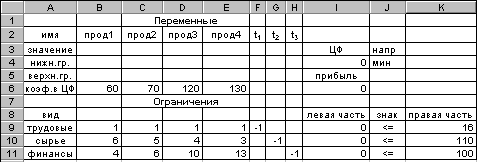
Рис. 3.3.14
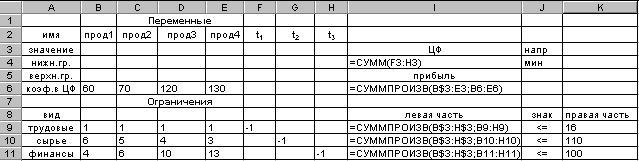
Рис. 3.3.15
На основі розглянутого можна записати наступний алгоритм.
Алгоритм 3.3.5. Подолання несумісності
1. Відкоригувати таблицю введення умові задачі (мал. 3.3.4), як це показано на мал. 3.3.14.
Увести для нових перемінних t1, t2, t3 стовпці F:H.
У комірках F9:H1 увести коефіцієнти -1, із якими ці перемінні входять в обмеження.
Увести нову цільову функцію в комірку 14, що варто мінімізувати.
Зауважимо, що формула старої цільової функції залишилася без змін.