3.3.3. Рішення задачі

Рішення задачі робиться відразу ж після введення даних по алг. 3.3.2, коли на екрані знаходиться діалогове вікно Пошук рішення (рис. 3.3.7).

Алгоритм 3.3.3. Рішення задачі лінійного програмування

1. Параметри...

На екрані: діалогове вікно Параметри пошуку рішення (мал. 3.3.9).

Рис. 3.3.9

За допомогою команд, що знаходяться в цьому діалоговому вікні, можна вводити умови для рішення задач оптимізації всіх класів. З найбільш важливими командами, застосовними при рішенні конкретних задач, ми будемо знайомитися в міру необхідності. Водночас, команди, використовувані по умовчанні, підходять для рішення більшої частини практичних задач.

Почнемо знайомство з командами, що можуть уводитися при рішенні задач усіх класів.

Максимальний час

Служить для призначення часу в секундах, що виділяється на пошук рішення задачі. У поле можна ввести час, що не перевищує 32767 із (більш 9 годин!). Значення 100, використовуване по умовчанні, підходить для рішення більшості задач.

Граничне число ітерацій

Служить для призначення числа ітерацій. Використовуване по умовчанні значення 100 підходить для рішення більшості задач.

Після цих пояснень продовжимо рішення задачі.

2. Установити прапорець Лінійна модель, що забезпечує застосування симплекса-методу.

3. ОК.

На екрані: знайоме вже діалогове вікно Пошук рішення (рис. 3.3.7).

4. Виконати.

На екрані: діалогове вікно Результати пошуку рішення. Рішення знайдене (рис. 3.3.10) і результат оптимального рішення задачі приведені в таблиці (рис. 3.3.11).

Рис. 3.3.10

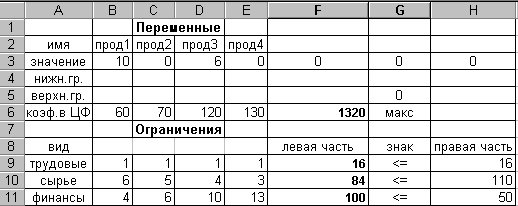
Рис. 3.3.11

На рис. 3.3.11 видно, що в оптимальнім рішенні

Прод1 = ВЗ = 10,

Прод2 = СЗ = ПРО,

Прод3 = D3 = 6,

Прод4 = ЕЗ = 0.

При цьому максимальний прибуток буде складати F6 = 1320, а кількість використаних ресурсів дорівнює

трудових = F9 =16,

сировини = F10 = 84,

фінансів = F11 = 100.

Таке оптимальне рішення розглянутої задачі розподілу ресурсів. Однак рішення задачі знаходиться не завжди. Якщо умови задачі несумісні, на екрані з'являється діалогове вікно (рис. 3.3.12).

Рис. 3.3.12

Необхідні дії в цьому випадку розглядаються в 3.3.5.

Якщо цільова функція не обмежена, то на екрані з'явиться діалогове вікно (мал. 3.3.13).

Рис. 3.3.13

Необхідні дії в цьому випадку розглядаються в 3.3.6.

3.3.4. Графічне представлення результатів рішення

Важливим фактором, що допомагає прийняти рішення, являється наочне представлення отриманого результату.

Результат рішення задачі, приведений на рис. 3.3.11, був прийнятий у якості вихідних даних при розгляді алгоритмів побудови диаграм різних типів у главі 2, розділі 2.2.

Діаграми, побудовані по цим даним, подані на мал. 2.2.8, 2.2.9, 2.2.13, 2.2.14, 2.2.16. Після одержання оптимального рішення розглянутої задачі ми настійно рекомендуємо уважно подивитися ці побудовані діаграми. Наведені діаграми убедительнее всяких слів доводять переваги наочного представлення результатів оптимального рішення.

3.3.5. Подолання несумісності

Як уже говорилося, досить часто при рішенні задач розподілу ресурсів умови задачі виявляються несумісними. Ми обіцяли сказати, що ж варто робити в таких випадках. Для цього розглянемо наступний приклад. У задачі, що ми вирішували, було отримано оптимальне рішення Прод1 = 10, Прод3 = 6. При цьому трудові ресурси і фінанси були використані цілком. Для одержання несумісності в навчальних цілях, змінимо умови задачі, зберігши значення невідомих, що ми одержали в оптимальному рішенні Прод1 = 10, Прод3 = 6. Додатково ще назначимо Прод2 = 5.

Очевидно, що для випуску такої кількості продукції ресурсів, що розташовуються, буде недостатньо. Подивимося, як вирішувати такі несумісні задачі за допомогою Excel. Насамперед уведемо зміну умов задачі.