Рішення завдань лінійного програмування за допомогою Excel Блок-схема рішення задачі

Послідовність необхідних робіт, виконуваних при рішенні задач лінійного програмування за допомогою Excel, наведена на блок-схемі (Рис. 3.3.1).

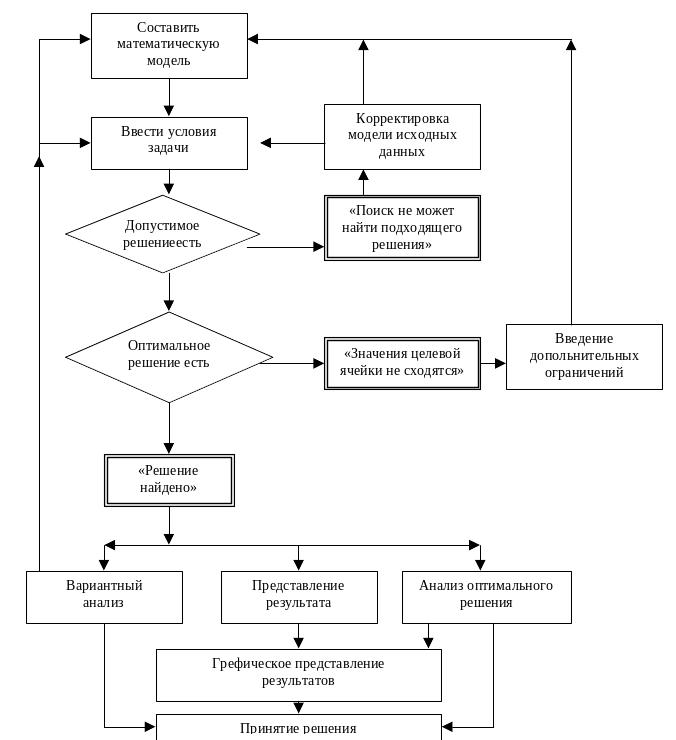
Рис. 3.3.1

Докладний опис цих робіт і складає утримування даної глави.

3.3.2. Введення умов задачі

Введення умов задачі складається з наступних основних кроків:

1. Створення форми для введення умов задачі.

2. Уведення вихідних даних.

3. Уведення залежностей із математичної моделі.

4. Призначення цільової функції.

5. Введення обмежень і граничних умов.

Послідовність робіт розглянемо на прикладі задачі розподілу ресурсів, вихідні дані якої наведені на рис. 3.1.6, а математична модель має вигляд (3.1.8).

Алгоритм 3.3.1. Уведення даних для рішення задачі лінійного програмування

1. Для задачі, наведеної на рис. 3.1.6, зробити форму для введення умов задачі (мал. 3.3.2).

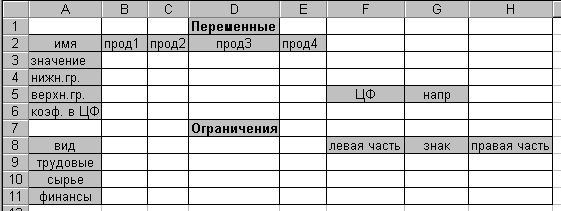
Рис. 3.3.2

Весь текст на рис. 3.3.2 (і надалі) являється коментарем і на рішення задачі не впливає.

2. Увести вихідні дані у форму (рис. 3.3.2).

Необхідні вихідні дані наведені на рис. 3.1.6.

Перехід від рис. 3.1.6 до рис. 3.3.2 показаний на рис. 3.3.3.

3. Увести залежності з математичної моделі (3.1.8).

Для наочності (але не обов'язково!) можна перейти до режиму представлення формул (алг. 2.1.12). При цьому введення даних доводиться на рис. 3.3.4, а режим представлення формул - на рис 3.3.5.

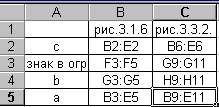
Рис. 3.3.3

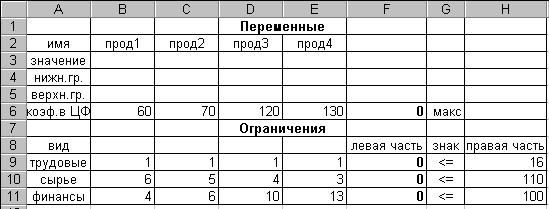
Рис. 3.3.4

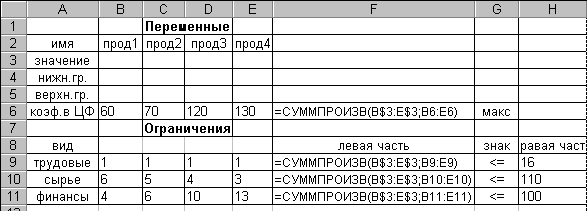
Рис. 3.3.5

3.1. Увести залежність для цільової функції:

• Курсор у F6.

• Курсор на кнопку Майстер функцій.

• М1.

На екрані: діалогове вікно Майстер функцій крок 1 із 2.

• Курсор у вікно Категорія на категорію Математичні.

• М1.

• Курсор у вікно Функції на СУММПРОИЗВ.

• М1.

• Далі.

На екрані: діалогове вікно (рис. 3.3.6).

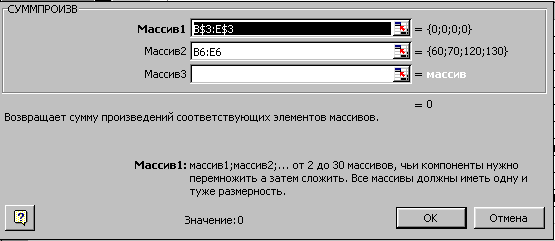
Рис. 3.3.6

• У масив 1 увести B$3:ES3.

Зауважимо, що в усі діалогові вікна адреси комірок зручно вводити не з клавіатури, а протягаючи мишу по комірках, чиї адреси варто ввести.

• У масив 2 увести В6:Е6.

• Готово.

На екрані: рис. 3.3.4, рис. 3.3.5 (у F6 уведені значення цільової функції).

3.2. Увести залежності для лівих частин обмежень:

• Курсор у F6.

• Копіювати в буфер.

• Курсор у F9.

• Уставити з буфера.

На екрані: у F9 уведена функція, як це показано на мал. 3.3.5.

• Скопіювати F9 у F10:F11.

На екрані: у F10:F11 уведені функції, як це показано на рис. 3.3.5.

На цьому введення даних у таблиці (мал. 3.3.4, мал. 3.3.5) закінчений.

Алгоритм 3.3.2. Робота в діалоговому вікні Пошук рішення

1. Сервіс, Пошук рішення...

На екрані: діалогове вікно Пошук рішення (рис. 3.3.7).

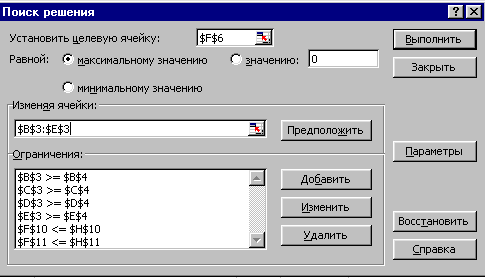
Рис. 3.3.7

2. Призначити цільову функцію:

• Курсор у вікно Установити цільову комірку.

• Ввести адресу: F6.

• Увести напрямок цільової функції: Максимальному значенню.

3. Ввести адреси шуканих перемінних:

• Курсор у поле Змінюючи комірки.

• Ввести адреси: ВЗ:ЕЗ.

4. Додати...

На екрані: діалогове вікно Додавання обмеження (рис. 3.3.8).

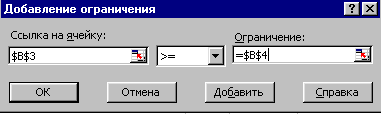
Рис. 3.3.8

5. Увести граничні умови на перемінні (Прод1 - Прод4)  0:

ВЗ >= В4, СЗ >= С4, D3 >= D4, ЕЗ >= Е4.

• У вікні Посилання на комірку увести ВЗ.

• Курсор на стрільцю.

• М1.

На екрані: знаки для введення в обмеження.

• Курсор на знак >=.

• > М1.

• Курсор у праве вікно.

• Увести В4.

• Додати...

На екрані: знову діалогове вікно Додавання обмеження (рис. 3.3.8).

Аналогічно ввести граничні умови для інших перемінних.

6. Аналогічно ввести обмеження:

F9<=H9, F10 <= Н10, F11 <=H11.

• Після введення останнього обмеження замість Додати... ввести ОК.

На екрані: діалогове вікно Пошук рішення з введеними умовами (рис. 3.3.7).

Якщо при введенні задачі виникає необхідність у зміні або видаленні внесених обмежень або граничних умові, то це робиться за допомогою команд Змінити..., Видалити.

На цьому введення умови задачі закінчується. На черзі наступний крок - рішення задачі.